BiLSTM-CRF模型中CRF层的运行原理(4)

前面我们重点介绍了CRF的原理，损失函数以及分数的计算。本节将结合前面的相关内容，介绍基于PyTorch(1.0)框架实现BILSTM-CRF模型及一些需要注意的细节。

模型总览

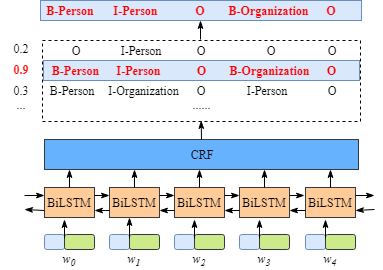
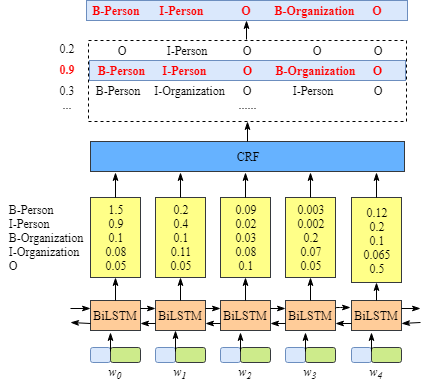
整个模型结构如下所示，我们也将按照该结构进行实现代码。

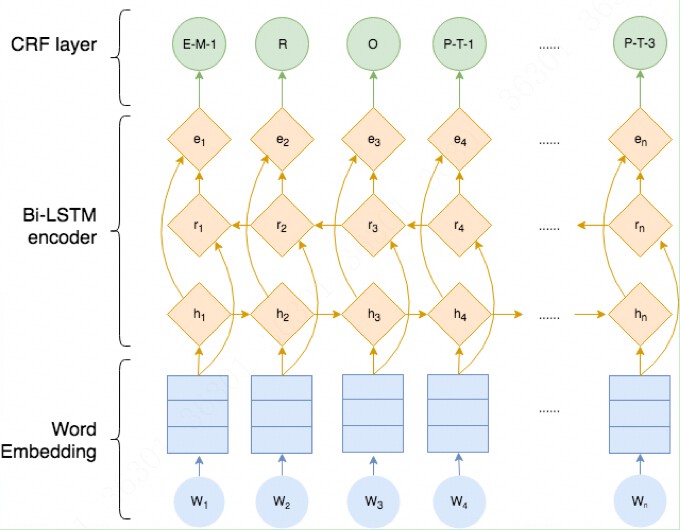
由上图可知，整个BILSTM-CRF模型由BILSTM、CRF、损失函数和预测函数几部分组成。BILSTM的输出作为CRF的输入，损失函数定义在CRF中，损失函数使用前向算法，预测函数使用Viterbi算法，下面逐一介绍。

class BILSTM_CRF(nn.Module):
    def __init__(self,
                 vocab_size,
                 word_embedding_dim,
                 word2id,
                 hidden_size, bi_flag,
                 num_layer, input_size,
                 cell_type, dropout,
                 num_tag, checkpoint_dir):
        super(BILSTM_CRF, self).__init__()

        self.embedding = nn.Embedding(vocab_size, word_embedding_dim)
        for p in self.embedding.parameters():
            p.requires_grad = False
        self.embedding.weight.data.copy_(torch.from_numpy(get_embedding(vocab_size,
                                                                        word_embedding_dim,
                                                                        word2id)))
        self.rnn = RNN(hidden_size, bi_flag,
                       num_layer, input_size,
                       cell_type, dropout, num_tag)
        self.crf = CRF(num_tag=num_tag)
        self.checkpoint_dir = checkpoint_dir

    def forward(self, inputs, length):
        embeddings = self.embedding(inputs)
        rnn_output = self.rnn(embeddings, length) #(batch_size, time_steps, num_tag+2)
        return rnn_output

    def loss_fn(self, rnn_output, labels, length):
        loss = self.crf.negative_log_loss(inputs=rnn_output, length=length, tags=labels)
        return loss

    def predict(self, rnn_output, length):
        best_path = self.crf.get_batch_best_path(rnn_output, length)
        return best_path

BILSTM

BILSTM模型这里采用的是双向LSTM。LSTM的输出（维度为 batch_size * time_steps * hidden_size）经过线性层（hidden_size * num_tag）变为(batch_size * time_steps * num_tag), 这是最终的输出结果。其中，hidden_size是LSTM隐藏层个数*2(因为是双向)， num_tag为需要标注的标签个数。

备注:

LSTM 参数说明:

num_layers: 表示几层的循环网络，默认为1
dropout：除了最后一层之外都引入一个dropout
batch_first：默认为False，因为nn.lstm接受的数据输入时(seq_len,batch_size,embed_dize),
如果为True，则转化为(batch_szie,seq_len.embed_size)
input_size: 输入数据的特征数
hidden_size：输出的特征数(hidden_size)

使用LSTM网络的使用方式，每一层LSTM都有三个外界的输入数据，即:

X；LSTM网络输入的数据
h_0: 上一层LSTM输出的结果
c_0: 上一层LSTM调整后的记忆

一般而言h_0和c_0初始化为0（每batch都会初始化为0）

LSTM的输出为：

（seq_len,batch,hidden_size * num_directions),
h_n: (num_layers * num_directions , batch_size, hidden_size)
c_n : (num_layers * num_directions , batch_size, hidden_size)

CRF

损失函数

对于一个句子，损失函数为这个句子的所有可能的路径得分之和减去真实路径得分。值得注意的是，这里的“路径”指的句子中的有小部分，不包括padding部分。

对于一个batch，我们将所有句子的损失函数相加，然后除以总的句子长度，将损失分配到每个字上，作为训练的损失函数。

这里的重点在于计算真实路径得分和所有路径得分之和，下面来看。

def negative_log_loss(self, inputs, length, tags):
    """
    features:(batch_size, time_step, num_tag)
    target_function = P_real_path_score/P_all_possible_path_score
                    = exp(S_real_path_score)/ sum(exp(certain_path_score))
    我们希望P_real_path_score的概率越高越好，即target_function的值越大越好
    因此，loss_function取其相反数，越小越好
    loss_function = -log(target_function)
                  = -S_real_path_score + log(exp(S_1 + exp(S_2) + exp(S_3) + ...))
                  = -S_real_path_score + log(all_possible_path_score)
    """
    if not self.use_cuda:
        inputs = inputs.cpu()
        length = length.cpu()
        tags = tags.cpu()

    loss = Variable(torch.tensor(0.), requires_grad=True)
    num_chars = torch.sum(length.data).float()      # 所有字的个数
    for ix, (features, tag) in enumerate(zip(inputs, tags)):
        features = features[:length[ix]]
        tag = tag[:length[ix]]
        real_score = self.real_path_score(features, tag)      # 真实路径得分
        total_score = self.all_possible_path_score(features)  # 所有可能的路径得分
        cost = total_score - real_score
        loss  = loss + cost
    return loss/num_chars             # 分配到每个字的损失

转移矩阵

在介绍得分计算之前，先来看下CRF中的一个重要的训练参数，转移矩阵。转移矩阵的定义决定了后面前向算法和维特比算法的实现，因此十分重要。

我们的标签序列id映射定义为：

tag_to_ix = {
    "B_PER": 0,   # 人名
    "I_PER": 1,
    "B_LOC": 2,   # 地点
    "I_LOC": 3,
    "B_ORG": 4,   # 机构
    "I_ORG": 5,
    "B_T": 6,     # 时间
    "I_T": 7,
    "O": 8,       # 其他
    "SOS": 9,     # 起始符
    "EOS":10      # 结束符
}

转移矩阵的大小为：(num_tag +2, num_tag +2)。+2是因为包含了起始符号和结束符号。

并且，P_jk 表示从tag_j到tag_k的得分，这样就有：

P_j $\star$ 表示所有从tag_j出发的边
P_ $\star$ k 表示所有到tag_k的边

此外，在均匀初始化时，设定起始符号和结束符号对应的转移分数，使得：

从EOS->其他标签为不可能事件, 如果发生，则产生一个极大的损失。
从其他标签->SOS为不可能事件，如果发生，则产生一个极大的损失。

def __init__(self, num_tag, use_cuda=False):
    if num_tag <= 0:
        raise ValueError("Invalid value of num_tag: %d" % num_tag)
    super(CRF, self).__init__()
    self.num_tag = num_tag
    self.start_tag = num_tag
    self.end_tag = num_tag + 1
    self.use_cuda = use_cuda
    # 转移矩阵transitions：P_jk 表示从tag_j到tag_k的分数
    # P_j* 表示所有从tag_j出发的边
    # P_*k 表示所有到tag_k的边
    self.transitions = nn.Parameter(torch.Tensor(num_tag + 2, num_tag + 2))
    nn.init.uniform_(self.transitions, -0.1, 0.1)
    self.transitions.data[self.end_tag, :] = -10000   # 表示从EOS->其他标签为不可能事件, 如果发生，则产生一个极大的损失
    self.transitions.data[:, self.start_tag] = -10000   # 表示从其他标签->SOS为不可能事件, 同上

真实路径得分

真实路径得分由Emission score和Transition score组成。其中，转移分数是CRF需要训练的参数，我们随机初始化；Emission score是BISTLM的输出矩阵（对于每个句子，其维度为 time_steps * num_tag），对于每个tag，该矩阵都给出一个score，我们知道了真实的标签序列，拿这个标签去索引该矩阵，即可得到真实路径的Emission score。

def real_path_score(self, features, tags):
    """
    features: (time_steps, num_tag)
    real_path_score表示真实路径分数
    它由Emission score和Transition score两部分相加组成
    Emission score由LSTM输出结合真实的tag决定，表示我们希望由输出得到真实的标签
    Transition score则是crf层需要进行训练的参数，它是随机初始化的，表示标签序列前后间的约束关系（转移概率）
    Transition矩阵存储的是标签序列相互间的约束关系
    在训练的过程中，希望real_path_score最高，因为这是所有路径中最可能的路径
    """
    r = torch.LongTensor(range(features.size(0)))
    if self.use_cuda:
        pad_start_tags = torch.cat([torch.cuda.LongTensor([self.start_tag]), tags])
        pad_stop_tags = torch.cat([tags, torch.cuda.LongTensor([self.end_tag])])
        r = r.cuda()
    else:
        pad_start_tags = torch.cat([torch.LongTensor([self.start_tag]), tags])
        pad_stop_tags = torch.cat([tags, torch.LongTensor([self.end_tag])])
    # Transition score + Emission score
    score = torch.sum(self.transitions[pad_start_tags, pad_stop_tags]).cpu() + torch.sum(features[r, tags])
    return score

所有路径分数之和

所有路径得分之和采用前向算法计算，算法复杂度为O(N * N * T)，其中N为标签个数，T为序列长度。

这里，将start_tag的Emission score初始化为0，从start_tag开始，沿着序列一个字一个字地计算前向分数。

最后，加上end_tag的Transition score，即为所有START_TAG -> 1st word -> 2nd word ->…->END_TAG的分数。

事实上，前向算法的精髓在于，用指数将每个字的得分用三个数存起来，而这三个数后面又是可以拆分的(指数的计算特性，乘法拆成加法。）

ps：如果对前向算法不是很明白或者大致明白但不是特别清晰，建议画个图看下就一目了然了。比如:

需要注意的是，根据前向算法，需要计算指数和的log，即 log_sum_exp，由于前向方法是一个不断累积的过程，会导致exp之和趋于无穷大，超过计算机的浮点数最大值限制，出现“上溢”。避免这种做法的手段是，找到整个矩阵的最大值，将矩阵减去该最大值进行指数求和，最终结果再加上该最大值即可。减去最大值后求指数和尽管也会出现无穷大的情况，但是这时是在分母上，该项可以计算为0，这样我们取log后仍可以得到一个合理的数值。

def all_possible_path_score(self, features):
    """
    计算所有可能的路径分数的log和：前向算法
    step1: 将forward列expand成9*9
    step2: 将下个单词的emission行expand成9*9
    step3: 将1和2和对应位置的转移矩阵相加
    step4: 更新forward，合并行
    step5: 取forward指数的对数计算total
    """
    time_steps = features.size(0)
    # 初始化
    forward = Variable(torch.zeros(self.num_tag))     # 初始化START_TAG的发射分数为0
    if self.use_cuda:
        forward = forward.cuda()
    for i in range(0, time_steps):  # START_TAG -> 1st word -> 2nd word ->...->END_TAG
        emission_start = forward.expand(self.num_tag, self.num_tag).t()
        emission_end = features[i,:].expand(self.num_tag, self.num_tag)
        if i == 0:
            trans_score = self.transitions[self.start_tag, :self.start_tag].cpu()
        else:
            trans_score = self.transitions[:self.start_tag, :self.start_tag].cpu()
        sum = emission_start + emission_end + trans_score
        forward = log_sum(sum, dim=0)
    forward = forward + self.transitions[:self.start_tag, self.end_tag].cpu()  # END_TAG
    total_score = log_sum(forward, dim=0)
    return total_score

def log_sum(matrix, dim):
    """
    前向算法是不断累积之前的结果，这样就会有个缺点
    指数和累积到一定程度后，会超过计算机浮点值的最大值，变成inf，这样取log后也是inf
    为了避免这种情况，我们做了改动：
    1. 用一个合适的值clip去提指数和的公因子，这样就不会使某项变得过大而无法计算
    SUM = log(exp(s1)+exp(s2)+...+exp(s100))
        = log{exp(clip)*[exp(s1-clip)+exp(s2-clip)+...+exp(s100-clip)]}
        = clip + log[exp(s1-clip)+exp(s2-clip)+...+exp(s100-clip)]
    where clip=max
    """
    clip_value = torch.max(matrix)                 # 极大值
    clip_value = int(clip_value.data.tolist())
    log_sum_value = clip_value + torch.log(torch.sum(torch.exp(matrix-clip_value), dim=dim))
    return log_sum_value

整个训练部分至此就介绍完了。下面介绍使用维特比算法进行预测。

预测

预测算法迭代过程和前向算法类似。不同的是，forward不再是到该点的路径得分之和，而是到该点的所有路径中最大得分，这样我们就有了到该点的最大路径。同时，在迭代过程中，我们将最大路径中到当前节点（具有最大分数）的前一个节点的索引存储下来，作为最佳路径点。

中间的迭代过程较容易理解，比较绕的是

如何处理起始符号和结束符号
最后一个节点怎么找

我们只需要把握一个点，上面的问题就能迎刃而解：

预测的时候，我们要从START_TAG -> 1st word -> 2nd word ->…->END_TAG，一个都不能少！

最后希望这张图能够帮助你理解算法中的细节。

    def viterbi(self, features):
        time_steps = features.size(0)
        forward = Variable(torch.zeros(self.num_tag))  # START_TAG
        if self.use_cuda:
            forward = forward.cuda()
        # back_points 到该点的最大分数  last_points 前一个点的索引
        back_points, index_points = [self.transitions[self.start_tag, :self.start_tag].cpu()], [torch.LongTensor([-1]).expand_as(forward)]
        for i in range(1, time_steps):  # START_TAG -> 1st word -> 2nd word ->...->END_TAG
            emission_start = forward.expand(self.num_tag, self.num_tag).t()
            emission_end = features[i,:].expand(self.num_tag, self.num_tag)
            trans_score = self.transitions[:self.start_tag, :self.start_tag].cpu()
            sum = emission_start + emission_end + trans_score
            forward, index = torch.max(sum.detach(), dim=0)
            back_points.append(forward)
            index_points.append(index)
        back_points.append(forward + self.transitions[:self.start_tag, self.end_tag].cpu())  # END_TAG
        return back_points, index_points

    def get_best_path(self, features):
        back_points, index_points = self.viterbi(features)
        # 找到线头
        best_last_point = argmax(back_points[-1])
        index_points = torch.stack(index_points)   # 堆成矩阵
        m = index_points.size(0)
        # 初始化矩阵
        best_path = [best_last_point]
        # 循着线头找到其对应的最佳路径
        for i in range(m-1, 0, -1):
            best_index_point = index_points[i][best_last_point]
            best_path.append(best_index_point)
            best_last_point = best_index_point
        best_path.reverse()
        return best_path

    def get_batch_best_path(self, inputs, length):
        if not self.use_cuda:
            inputs = inputs.cpu()
            length = length.cpu()
        max_len = inputs.size(1)
        batch_best_path = []
        for ix, features in enumerate(inputs):
            features = features[:length[ix]]
            best_path = self.get_best_path(features)
            best_path = torch.Tensor(best_path).long()
            best_path = padding(best_path, max_len)
            batch_best_path.append(best_path)
        batch_best_path = torch.stack(batch_best_path, dim=1)
        return batch_best_path

def argmax(matrix, dim=0):
    """(0.5, 0.4, 0.3) —> 0"""
    _, index = torch.max(matrix, dim=dim)
    return index

def padding(vec, max_len, pad_token=-1):
    new_vec = torch.zeros(max_len).long()
    new_vec[:vec.size(0)] = vec
    new_vec[vec.size(0):] = pad_token
    return new_vec