条件随机场-CRF

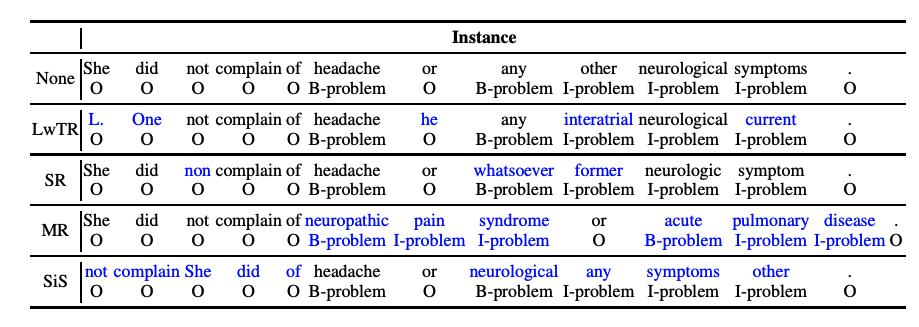
最近一段时间在研究NER相关项目，因此，打算对NER一些算法做一定总结，本文主要记录自己在学习CRF模型过程中的一些记录，大部分来自于网上各位大神的博客。

什么样的问题需要CRF模型

假设你有许多小明同学一天内不同时段的照片，从小明提裤子起床到脱裤子睡觉各个时间段都有（小明是照片控！）。现在的任务是对这些照片进行分类。比如有的照片是吃饭，那就给它打上吃饭的标签；有的照片是跑步时拍的，那就打上跑步的标签；有的照片是开会时拍的，那就打上开会的标签。问题来了，你准备怎么干？

一个简单直观的办法就是，不管这些照片之间的时间顺序，想办法训练出一个多元分类器。就是用一些打好标签的照片作为训练数据，训练出一个模型，直接根据照片的特征来分类。例如，如果照片是早上6:00拍的，且画面是黑暗的，那就给它打上睡觉的标签;如果照片上有车，那就给它打上开车的标签。

这样可行吗？

乍一看可以！但实际上，由于我们忽略了这些照片之间的时间顺序这一重要信息，我们的分类器会有缺陷的。举个例子，假如有一张小明闭着嘴的照片，怎么分类？显然难以直接判断，需要参考闭嘴之前的照片，如果之前的照片显示小明在吃饭，那这个闭嘴的照片很可能是小明在咀嚼食物准备下咽，可以给它打上吃饭的标签；如果之前的照片显示小明在唱歌，那这个闭嘴的照片很可能是小明唱歌瞬间的抓拍，可以给它打上唱歌的标签。

所以，为了让我们的分类器能够有更好的表现，在为一张照片分类时，我们必须将与它相邻的照片的标签信息考虑进来。这——就是条件随机场(CRF)大显身手的地方！

CRF算法

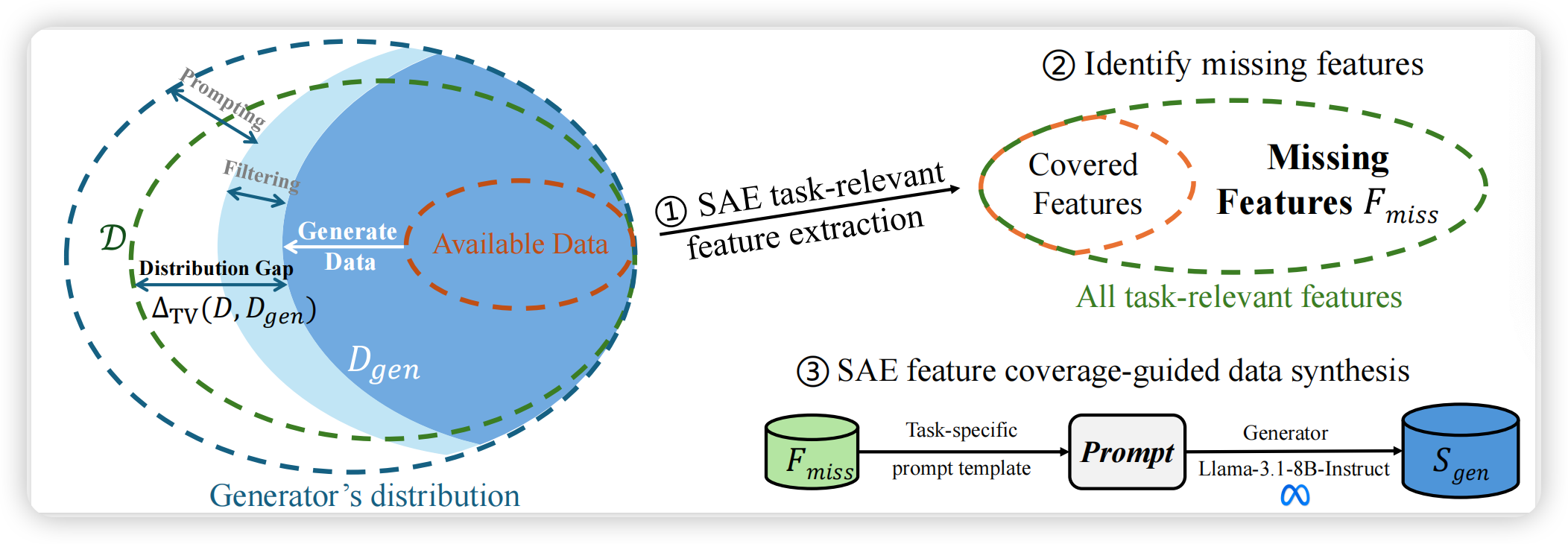
条件随机场（Conditional random field ,CRF) 是条件概率分布模型P(X|Y)，表示的是给定一组随机输入向量X的条件下另一组输出随机向量Y的马尔可夫随机场，也就是说CRF的特点是假设输出随机变量构成马尔可夫随机场。

下图可以很好地展示CRF模型与其他模型的区别：

由于CRF本质上是一个序列分类器，我们知道循环神经网络也可以对序列进行分类，那么两者是否有关联？

从两个模型之间的结构来看，我们可以发现两者都利用了数据之间的时序信息。不同的是，RNN中具有一些未知的潜在状态（比如LSTM中的存储器)，而CRF是针对训练数据已知的潜在状态（模型必须学习如何为测试数据预测哪些潜在状态）。

基本结构

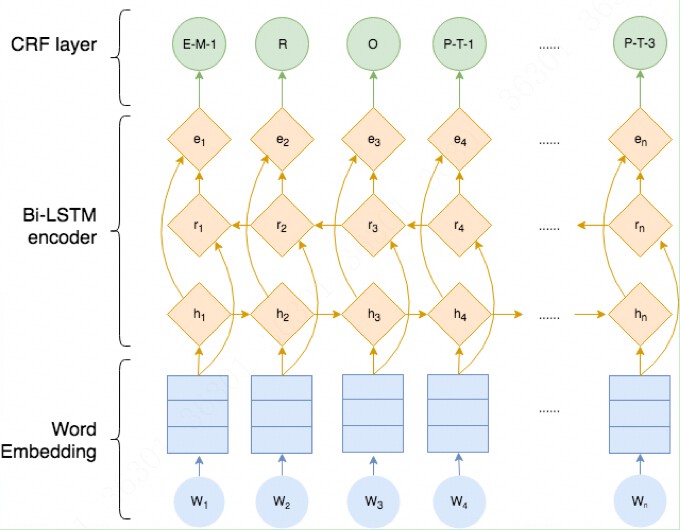
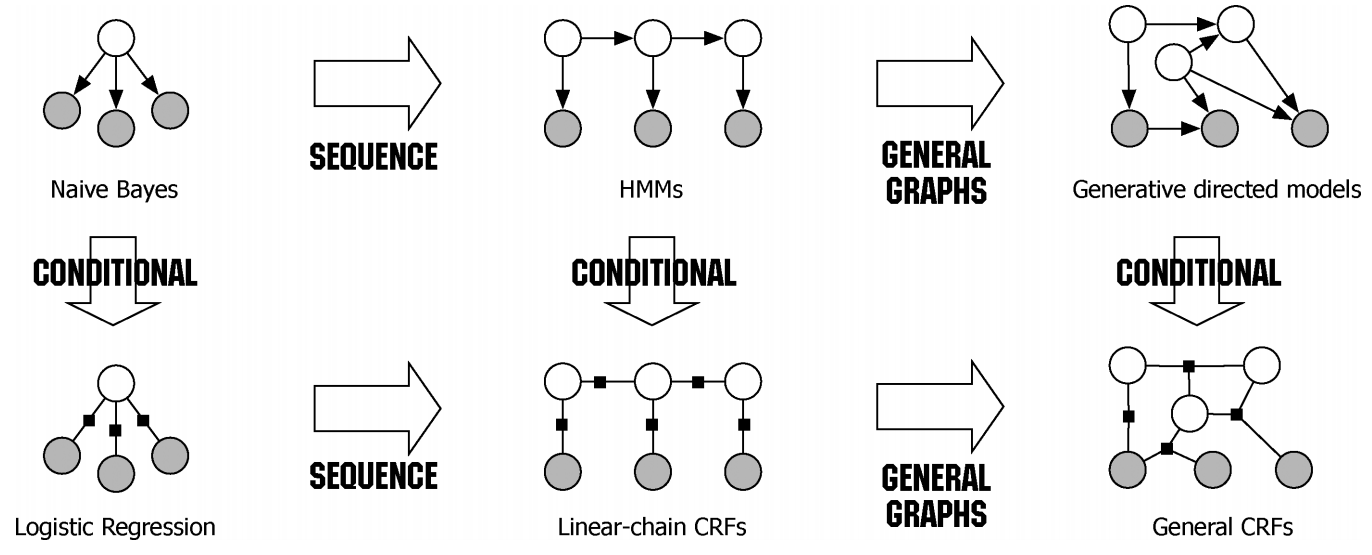
CRF的基本结构如下图所示：

给定输入序列（例如，单词）向量x，标签序列（例如，词性）向量y出现的概率被定义为： 与最大熵模型（逻辑回归）完全相同（唯一不同的是最大熵模型是对单个变量进行分类，则CRF模型是对序列进行分类）。具体的计算公式如下:

$${ p }\left( y | x \right) =\frac { 1 }{ { Z }\left( x \right) } \cdot exp\left( \sum _{ j=1 }^{ n }{ \sum _{ i=1 }^{ m }{ { \lambda }_{ i }{ f }_{ i }\left( { y }_{ j-1 },{ y }_{ j }, x ,j \right) } } \right)$$

其中 Z(x) 是归一化因子，因为这个是条件分布，所以归一化因子跟 x 有关。这个 f 函数可以视为一个打分函数，打分函数取指数并归一化后就得到概率分布。

从上述公式中，我们可以看到:

• 该分布是指数分布
• 输出之间的关联仅发生在相邻位置，并且关联是指数加性的

接下来，我们使用python实现上述计算公式：

import math
def calc_prob_y_given_x(y_prime, x, all_labels, FeatureFunction, weights):
    n = len(y_prime)
    m = len(weights)
    nominator = 0
    for j in range(1, n):
        for i in range(1, m):
            nominator += weights[i] * FeatureFunction(y_prime, x, i, j) # 求和部分
    denominator = calc_Z(x, n, m, all_labels, FeatureFunction, weights)# 计算归一化因子
    return math.exp(nominator) / denominator # 归一化

其中:

• y_prime: 标记序列
• x: 观察序列
• all_labels: 标签列表
• FeatureFunction: 特征函数
• weights: 权重列表

特征函数

我们可以很灵活地对CRF模型设置诸如最大熵模型或最大熵标记模型之类的特征，比如：

# x : words (观察序列)
# y : lables (例如: POS TAGS, 标记序列)
def FeatureFunction(x, y, i, j):
    # f_1
    if i == 1 and y[j-1] == 'NN': #名词
        return 1
    # f_2
    elif i == 2 and y[j-1] == 'VBZ': #动词第三人称单数
        return 1
    # f_3
    elif i == 3 and x[0] == 'DT': # 限定词
        return 1
    else:
        return 0

归一化

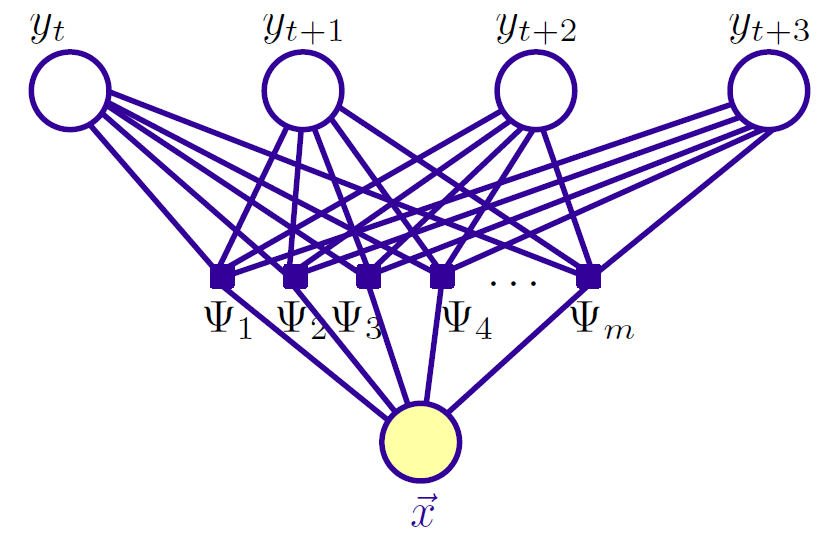
‘归一化’操作可以解决标签偏置问题，比如：

路径1-1-1-1的概率：0.40.450.5=0.09

路径2-2-2-2的概率:0.018

路径1-2-1-2:0.06

路径1-1-2-2:0.066

由此可得最优路径为1-1-1-1

而实际上，在上图中，状态1偏向于转移到状态2，而状态2总倾向于停留在状态2，这就是所谓的标注偏置问题，由于分支数不同，概率的分布不均衡，导致状态的转移存在不公平的情况。

为了解决该问题，通过归一化计算，我们可以得到不同标记序列之间的相对概率大小（最大概率对应的标记序列就是模型预测为最有可能的结果），具体的Z(X)计算公式如下:

$$Z(x) = \sum_y \exp (\sum_{j=1}^n \sum_{i=1}^m w_i f_i (y_{j-1},y_{j},x,j))$$

具体的python实现代码如下：

def calc_Z(x, n, m, all_labels, FeatureFunction, weights):
    Z = 0
    all_possible_Y = itertools.product(all_labels, repeat=n) # 所有标记组合序列
    for y_prime in all_possible_Y:　＃　遍历标记组合
        tmpZ = 0
        for j in range(1, n):
            for i in range(1, m):
                tmpZ += weights[i] * FeatureFunction(y_prime, x, i, j)# 计算公式
        Z += math.exp(tmpZ)
    return Z

通过上述代码，我们获得所有可能组合的标签序列的概率。 例如，假设词性类型是名词（NN），动词（VB），并且序列长度是5个单词，则我们需要计算5^5 = 3125个标记序列的概率，如下表所示：

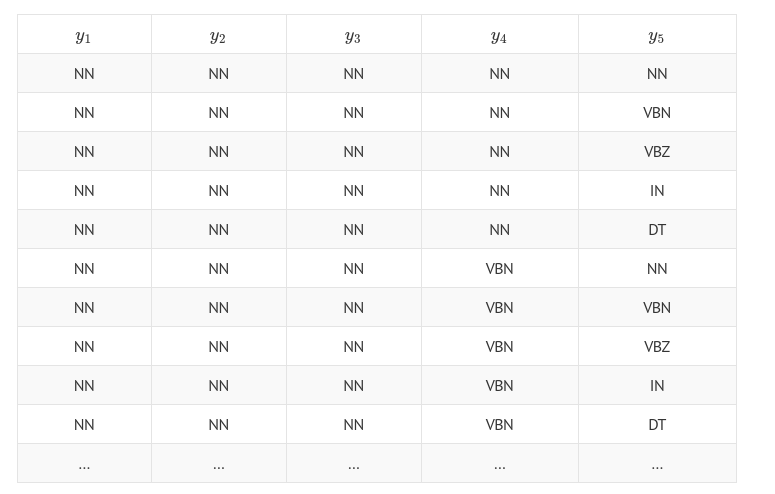
CRF的计算难度是在计算Z(X)的部分，上述代码只是为了帮助理解，在实际中会使用一些优化技术进行实现。

参数学习：最大似然估计

为了训练 CRF 模型，我们用最大似然方法，也就是用：

$$-\log p(y|x)$$

作为损失函数，则CRF模型的对数似然函数如下：

其中第一项是原来概率式的分子的对数，它目标的序列的打分，虽然它看上去挺迂回的，但是并不难计算。真正的难度在于分母的对数 logZ(x) 这一项。

** 注意** : 表达式第一行中的第二项是为了防止过拟合增加的正则项。

类似于逻辑回归模型训练方法，我们通过最大似然估计方法可以获得CRF模型的参数。

当对数似然函数在参数$\lambda$的偏微分值为0时可以获得最大值。从原式中，我们可以发现主要分成三部分，接下来我们分析每部分对于参数$\lambda$的微分。

A的部分对于参数$\lambda$的偏导结果如下：

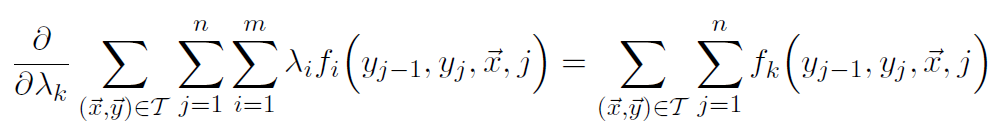
B部分对于参数$\lambda$的偏导结果如下：

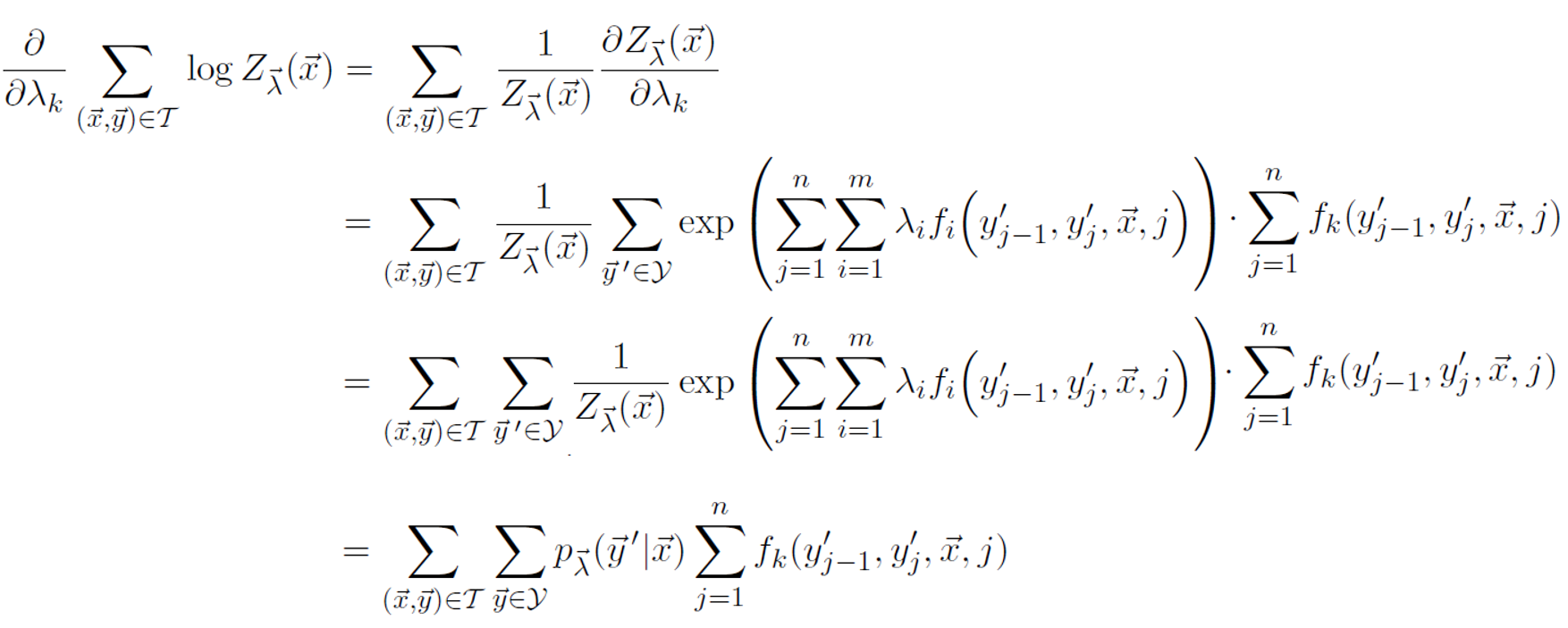
C部分对于参数$\lambda$的偏导结果如下：

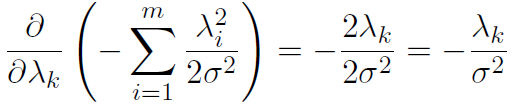
其中A部分我们可以理解为数据的经验分布，即：

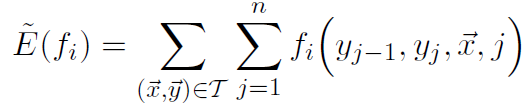
具体的python实现代码如下：

def calc_empirical_expectation_feature_i(train_data, FeatureFunction, i):
    empirical_expectation_feature_i = 0
    for x, y in train_data:
        n = len(y)
        for j in range(1, n):
            empirical_expectation_feature_i += FeatureFunction(y, x, i, j)
    return empirical_expectation_feature_i

B部分我们可以解释为模型的分布，即：

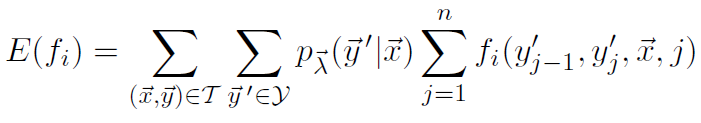
具体的python实现代码如下：

import itertools
def calc_predicted_expectation_feature_i(train_data, FeatureFunction, 
									  all_labels, weights, i):
    predicted_expectation = 0
    for x, y in train_data:
        n = len(y)
        all_possible_Y = itertools.product(all_labels, repeat=n)
        for y_prime in all_possible_Y:
            predicted_expectation += \
                (calc_prob_y_given_x(y_prime, x, all_labels, FeatureFunction, weights)
                 * sum([FeatureFunction(x, y, i, j) for j in range(1, n)]))
            print(predicted_expectation)
    return predicted_expectation

如果我们重写对数似然函数的偏微分方程，即：

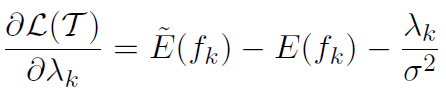
A和B越近，对数似然函数的导数越小。数据的分布和模型的分布越相似，模型就越能模拟数据的分布。

以上我们差不多构建完了整个模型部分，在随机初始化参数$\lambda$之后，我们就可以对参数$\lambda$进行迭代更新。

具体的python实现代码如下:

#train data set = {(x, y)}
def get_all_labels(train_data):
    available_labels = set()
    for x, y in train_data:
        available_labels.update(y)
    return list(available_labels)

# m = feature vector size
import random
def initial_weights(m):
    return [random.random() for _ in range(m)]
   
def train(train_data, FeatureFunctions, m, iterations=100, learning_rate=0.1):
    all_labels = get_all_labels(train_data)
    weights = initial_weights(m)
    for _ in range(iterations):
        for i in range(1, m):
            empirical_expectation = \
                calc_empirical_expectation_feature_i(train_data, FeatureFunction, i)
            predicted_expectation = \
                calc_predicted_expectation_feature_i(train_data, FeatureFunction,
                                                     all_labels, weights)
            weights[i] = weights[i] + \
            			learning_rate * (empirical_expectation - predicted_expectation)

预测算法：维特比算法

条件随机场的预测问题是给定条件条件随机场P(y|x)和输入序列x，求条件概率最大的输出序列y，即对观测序列进行标注，条件随机场的预测算法是著名的维特比算法。

维特比算法是一个特殊且应用最广的动态规划算法。利用动态规划，可以解决任何一个图中的最短路径问题。而维特比算法是针对一个特殊的图——篱笆网络的有向图（Lattice) 的最短路径问题而提出的。

维特比算法的基础可以概括为下面三点：

• 1.如果概率最大的路径经过篱笆网络的某点，则从开始点到该点的子路径也一定是从开始到该点路径中概率最大的。
• 2.假定第i时刻有k个状态，从开始到i时刻的k个状态有k条最短路径，而最终的最短路径必然经过其中的一条。
• 3.根据上述性质，在计算第i+1状态的最短路径时，只需要考虑从开始到当前的k个状态值的最短路径和当前状态值到第i+1状态值的最短路径即可，如求t=3时的最短路径，等于求t=2时的所有状态结点$x_{2i}$的最短路径加上t=2到t=3的各节点的最短路径。

比如，假设病人连续三天看医生，医生发现第一天他感觉正常，第二天感觉冷，第三天感觉头晕。 于是医生产生了一个问题：怎样的健康状态序列最能够解释这些观察结果。维特比算法解答了这个问题。

首先直观地看这个问题，在HMM中，一个观测现象后面的对应的各个状态都有一个概率值，我们只需要选择概率值最大的那个状态即可，但是这个概率值是跟前面一个状态有关的（马尔科夫假设），因此不能独立考虑每个观测现象。

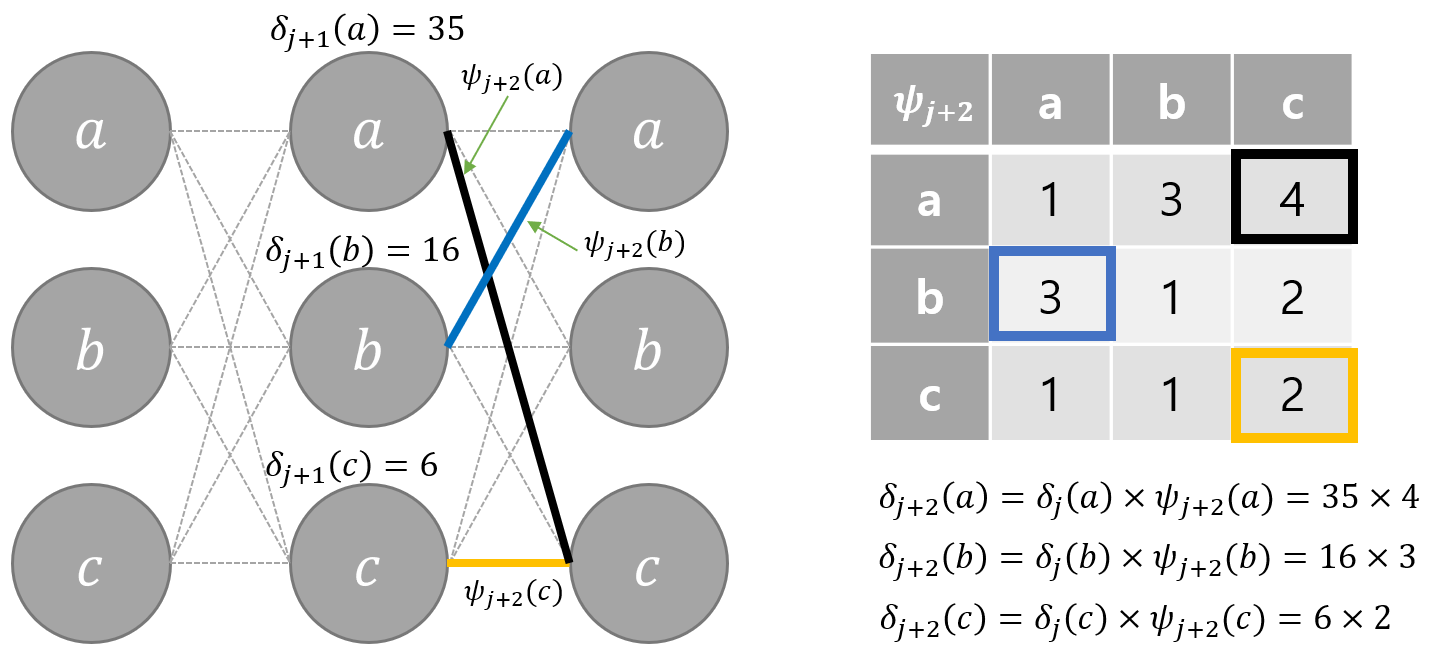
为了从时间复杂度方面进行比较，现在将问题一般化：假设观测序列的长度为 m，隐含状态个数为 n。则有下面的隐含状态转移图（下图为了便于表示，将只画出n = 3 的图）。

假如采用穷举法，穷举出所有可能的状态序列再比较他们的概率值，则时间复杂度是 O(n^m), 显然这样的时间复杂度是无法接受的，而通过维特比算法能把时间复杂度降到 O(m∗n^2)

从动态规划的问题去考虑这个问题，根据上图的定义，记 last_state 为上一个观测现象对应的各个隐含状态的概率，curr_state 为现在的观测现象对应的各个隐含状态的概率。则求解curr_state实际上只依赖于last_state。而他们的依赖关系可通过下面的 python 代码表示出来:

for cs in states:
    curr_state[cs] = max(last_state[ls] * 
                         transition_probability[ls][cs] *             
                         emission_probability[cs][observation] 
                         for ls in states)

计算过程利用了转移概率 transition_probability 和发射概率 emission_probability，选出那个最有可能产生当前状态 cs 的上一状态 ls。

除了上面的计算，同时要为每个隐含状态维护一个路径 path， path[s] 表示到达状态 s 前的最优状态序列。通过前面的计算选出那个最有可能产生当前状态 cs 的上一状态 ls后，往path[cs] 中插入 ls。则依照这种方法遍历完所有的观测序列后，只需要选择 curr_state 中概率值最大的那个 state 作为最终的隐含状态，同时从 path 中取出 path[state] 作为该最终隐含状态前面的状态序列。

从上面的分析可知，观测序列只需要遍历一遍，时间复杂度为 O(m)，而每次要计算当前各个状态最可能的前一状态，时间复杂度为 O(n^2),因此总体的时间复杂度为 O(m∗n^2).

另外，假如在 NLP 中应用 HMM，则将词序列看做是观测到的现象，而词性、标签等信息看做是隐含状态，那么就可以通过维特比算法求解其隐含状态序列，而这也是 HMM 在分词，词性标注，命名实体识别中的应用。其关键往往是找出上面提到的初始概率（start_probability）、转移概率（transition_probability）、发射概率（emission_probability）。

而在通信领域中，假如将收到的编码信息看作是观测序列，对应的解码信息为隐含状态，那么通过维特比算法也能够找出概率最大的解码信息。

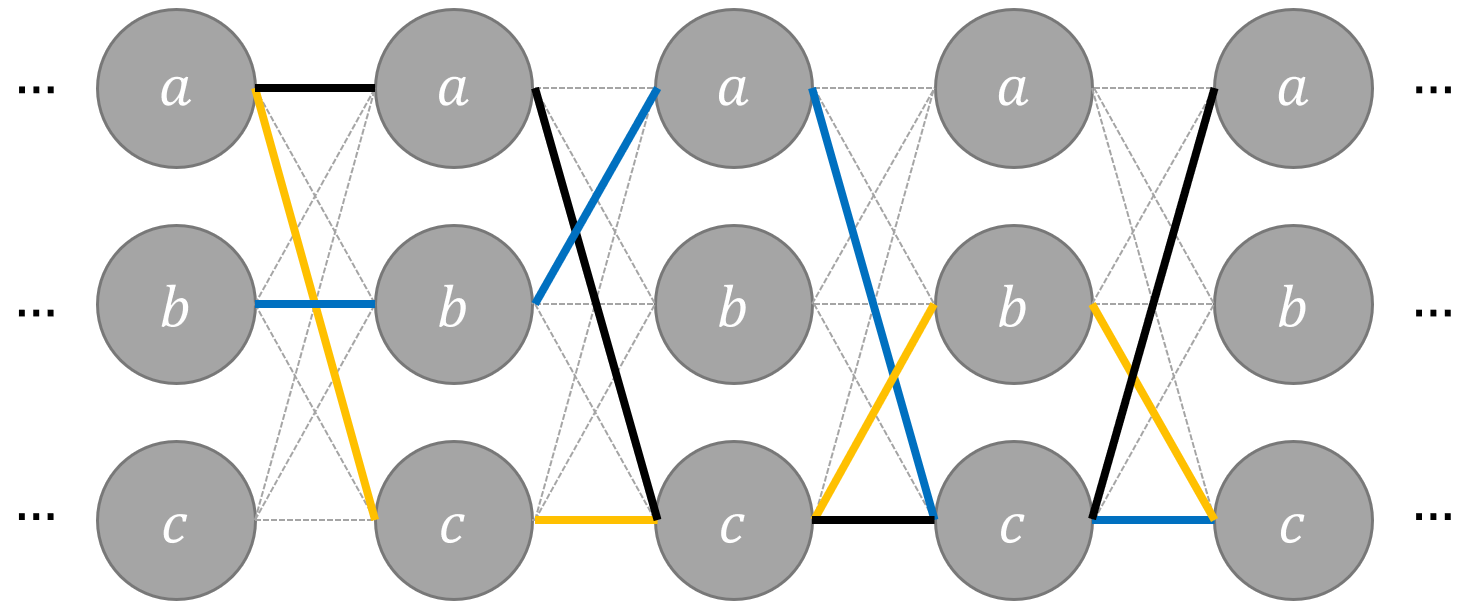
需要注意的是维特比算法适用于多步骤多选择的最优问题，类似于下面的网络，《数学之美》中将其叫做“篱笆网络(Lattice)”。每一步都有多个选择，并且保留了前面一步各个选择的最优解，通过回溯的方法找到最优选择路径。

这里要强调的是 viterbi 算法可以用于解决 HMM 问题，但是也可以用于解决其他符合上面描述的问题。

下面，我们来具体看看，其工作原理如下。

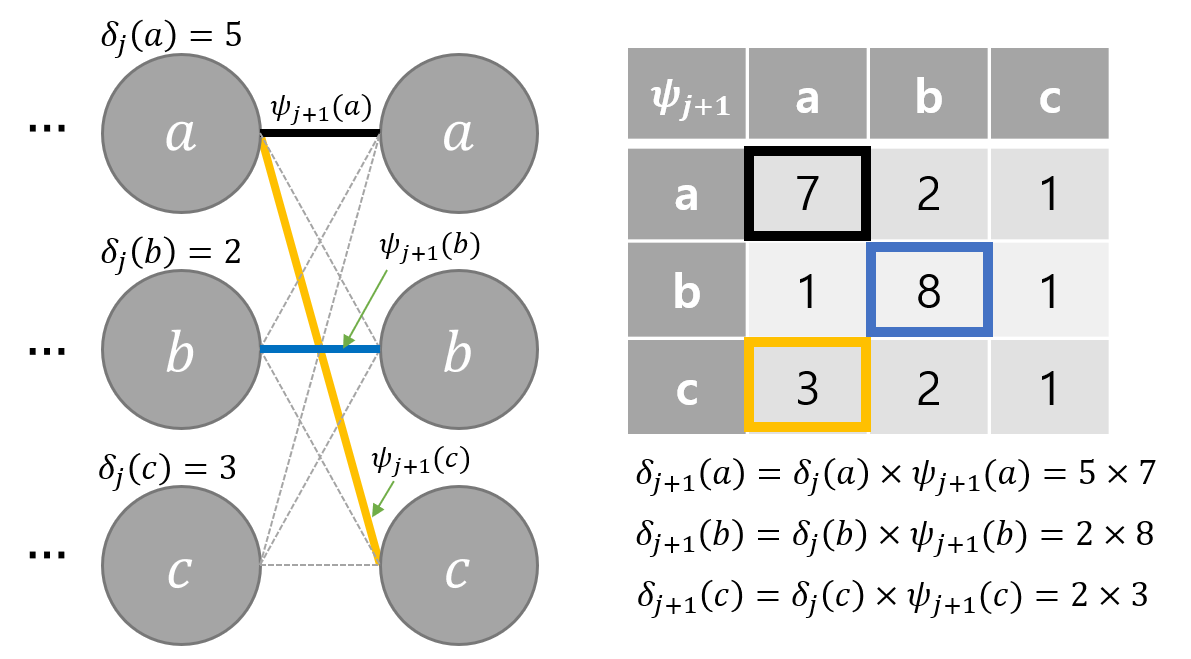
下一步：

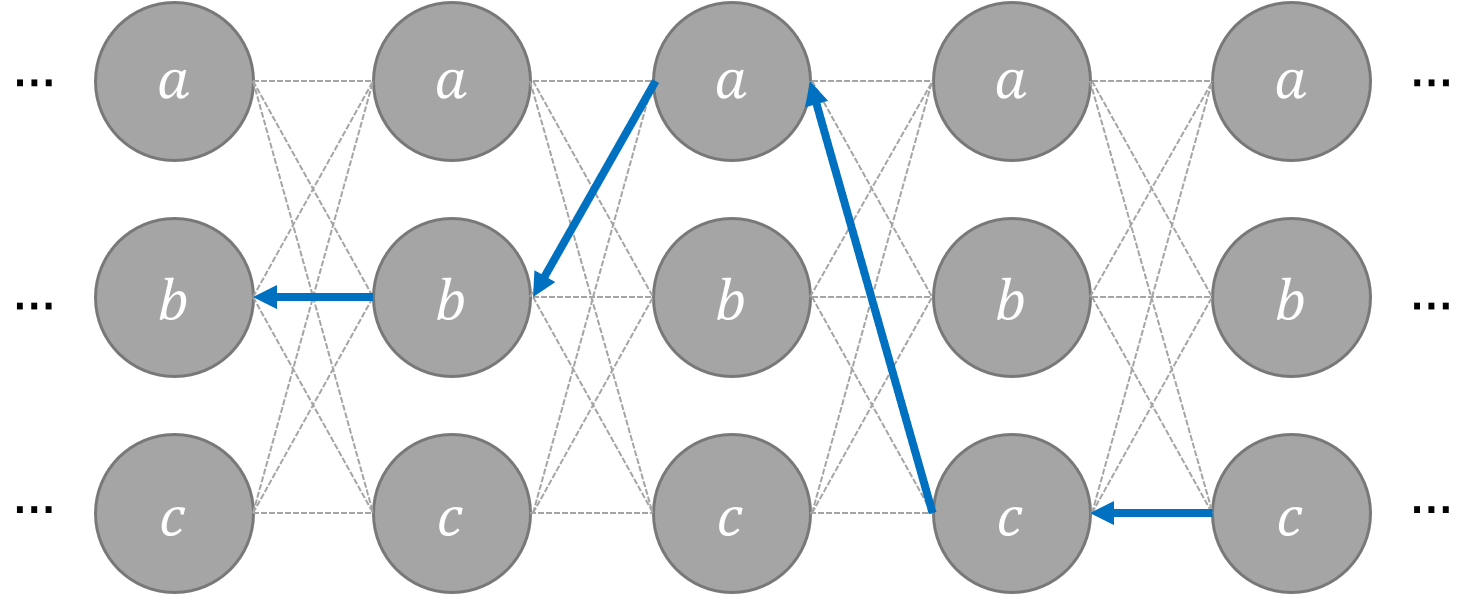
下一步：

最后，回溯过程，即反向获取每一路径的最优状态，然后将所有结果组合成最后的预测结果

上述，我们介绍完了整个CRF算法的理论原理，接下来，我们来看看CRF模型怎么处理词性标注问题。

词性标注问题

啥是词性标注问题？

非常简单的，就是给一个句子中的每个单词注明词性。比如这句话：“Bob drank coffee at Starbucks”，注明每个单词的词性后是这样的：“Bob (名词) drank(动词) coffee(名词) at(介词) Starbucks(名词)”。

下面，就用条件随机场来解决这个问题。

以上面的话为例，有5个单词，我们将：(名词，动词，名词，介词，名词)作为一个标注序列，称为l，可选的标注序列有很多种，比如y还可以是这样：（名词，动词，动词，介词，名词），我们要在这么多的可选标注序列中，挑选出一个最靠谱的作为我们对这句话的标注。

怎么判断一个标注序列靠谱不靠谱呢？

就我们上面展示的两个标注序列来说，第二个显然不如第一个靠谱，因为它把第二、第三个单词都标注成了动词，动词后面接动词，这在一个句子中通常是说不通的。

假如我们给每一个标注序列打分，打分越高代表这个标注序列越靠谱，我们至少可以说，凡是标注中出现了动词后面还是动词的标注序列，要给它负分！！

上面所说的动词后面还是动词就是一个特征函数，我们可以定义一个特征函数集合，用这个特征函数集合来为一个标注序列打分，并据此选出最靠谱的标注序列。也就是说，每一个特征函数都可以用来为一个标注序列评分，把集合中所有特征函数对同一个标注序列的评分综合起来，就是这个标注序列最终的评分值。

定义特征函数

现在，我们正式地定义一下什么是CRF中的特征函数，所谓特征函数，就是这样的函数，它接受四个参数：

• 句子s（就是我们要标注词性的句子）
• i，用来表示句子s中第i个单词
• y_i，表示要评分的标注序列给第i个单词标注的词性
• y_i-1，表示要评分的标注序列给第i-1个单词标注的词性

它的输出值是0或者1,0表示要评分的标注序列不符合这个特征，1表示要评分的标注序列符合这个特征。

Note:这里，我们的特征函数仅仅依靠当前单词的标签和它前面的单词的标签对标注序列进行评判，这样建立的CRF也叫作线性链CRF，这是CRF中的一种简单情况。为简单起见，本文中我们仅考虑线性链CRF。

从特征函数到概率

定义好一组特征函数后，我们要给每个特征函数f_j赋予一个权重λ_j。现在，只要有一个句子x，有一个标注序列y，我们就可以利用前面定义的特征函数集来对l评分。

$$score(y|x) =\sum_{j=1}^m \sum_{i = 1}^n \lambda_j f_j(x,i,y_i,y_{i-1})$$

上式中有两个求和，外面的求和用来求每一个特征函数f_j评分值的和，里面的求和用来求句子中每个位置的单词的的特征值的和.

对这个分数进行指数化和标准化，我们就可以得到标注序列l的概率值p(y|x)，如下所示：

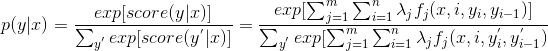
几个特征函数的例子

前面我们已经举过特征函数的例子，下面我们再看几个具体的例子，帮助增强大家的感性认识。

$$f_{1}(s,i,y_i,y_{i-1}) = 1$$

当y_i是“副词”并且第i个单词以“ly”结尾时，我们就让f1 = 1，其他情况f1为0。不难想到，f1特征函数的权重λ1应当是正的。而且λ1越大，表示我们越倾向于采用那些把以“ly”结尾的单词标注为“副词”的标注序列

$$f_{2}(s,i,y_i,y_{i-1}) = 1$$

如果i=1，y_i=动词，并且句子s是以“？”结尾时，f2=1，其他情况f2=0。同样，λ2应当是正的，并且λ2越大，表示我们越倾向于采用那些把问句的第一个单词标注为“动词”的标注序列。

$$f_{3}(s,i,y_i,y_{i-1}) = 1$$

当y_i-1是介词，y_i是名词时，f3 = 1，其他情况f3=0。λ3也应当是正的，并且λ3越大，说明我们越认为介词后面应当跟一个名词。

$$f_{4}(s,i,y_i,y_{i-1}) = 1$$

如果y_i和y_i-1都是介词，那么f4等于1，其他情况f4=0。这里，我们应当可以想到λ4是负的，并且λ4的绝对值越大，表示我们越不认可介词后面还是介词的标注序列。

好了，一个条件随机场就这样建立起来了，让我们总结一下：
为了建一个条件随机场，我们首先要定义一个特征函数集，每个特征函数都以整个句子s，当前位置i，位置i和i-1的标签为输入。然后为每一个特征函数赋予一个权重，然后针对每一个标注序列l，对所有的特征函数加权求和，必要的话，可以把求和的值转化为一个概率值。