BiLSTM模型中CRF层的运行原理(2)

在上一节中，我们知道CRF层可以从训练数据集中自动学习到一些约束规则来保证预测标签的合法性。这些约束包括：

• 句子中第一个词总是以标签“B-“ 或 “O”开始，而不是“I-”
• 标签“B-label1I-label2 I-label3 I-…”,label1, label2, label3应该属于同一类实体。例如，“B-PersonI-Person” 是合理的序列, 但是“B-Person I-Organization” 是不合理标签序列.
• 标签序列“O I-label”是不合理的，实体标签的首个标签应该是 “B-“ ，而非 “I-“, 换句话说，有效的标签序列应该是“O B-label”。

这一节，我们将解释为什么CRF层会自动学习到这些约束规则。

1.CRF层

在CRF层损失函数中，有两种形式的score。这些scores是CRF层的关键概念。

1.1 emission score

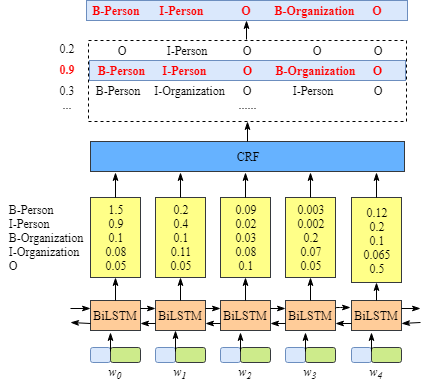
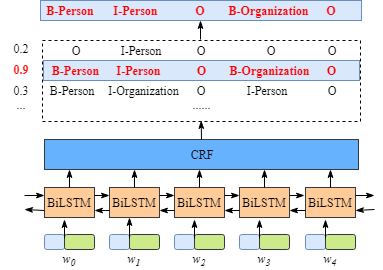
第一个是emission score，主要来自BiLSTM层的输出，如下图所示，比如，单元$w_0$标记为‘B-Person’的score为1.5：

为了方便起见，我们用数字来表示各个实体标签，对应关系如下：

Label	Index
B-Person	0
I-Person	1
B-Organization	2
I-Organization	3
O	4

另外，我们使用$x_{iy_j}$表示emission score，其中:

• i 表示词的索引
• $y_j$表示标签的索引

例如，根据上图，我们可以得到$x_{i=1,y_j=2} = x_{w_1,B-Organization} = 0.1$，也就是说$w_1$标记为’B-Organization‘的score为0.1。

1.2 Transition score

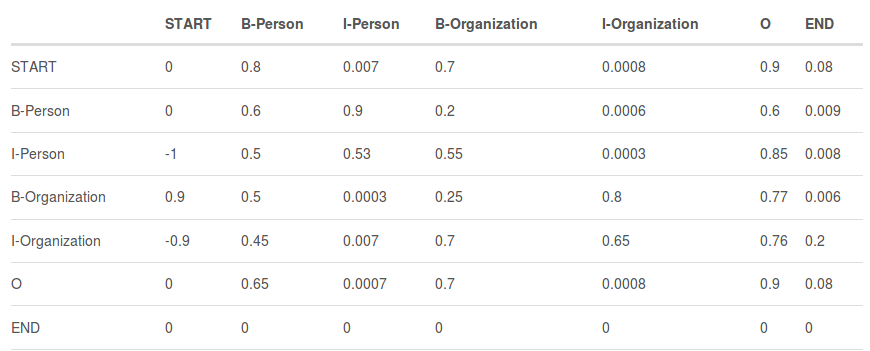
我们定义$t_{y_iy_j}$表示transition score，从上图中可知$t_{B-Person,I-Person} = 0.9$，也就是说“$B-Person \rightarrow I-Person$“的标签转移得分为0.9。因此，对于所有的标签序列组合，我们将得到一个transition score矩阵，包含了所有标签之间的transition score。

为了使transition score矩阵更具鲁棒性，我们额外增加两个标签——START 和END，START 代表句子的开始位置，而非第一个词，同理，END代表句子的结束位置.

表1 中包含了START和END标签的transition score矩阵。

如表1所示，我们可以发现transition score矩阵可以学习到好多约束规则，比如:

• 句子中第一个词总是以标签“B-“ 或 “O”开始，而不是“I-”（例如，从“START” 到 “I-Person or I-Organization”的score都很低 ）。
• 标签“B-label1I-label2 I-label3 I-…”,label1, label2, label3应该属于同一类实体。例如，“B-Person I-Person” 是合理的序列, 但是“B-Person I-Organization” 是不合理的标签序列（例如，从“B-Organization”到’I-Person’的score只有0.0003，比其他都低。）。
• 标签序列“O I-label” 是不合理的.实体标签的首个标签应该是 “B-“ ，而非 “I-“, 换句话说,有效的标签序列应该是“O B-label”（例如，$t_{O,I-Person}$的score就非常小）。

你可能会有一个疑问，该transition score矩阵如何计算得到？

事实上，该矩阵是BiLSTM-CRF模型的一个参数，在训练模型之前，一般会初始化一个矩阵作为transition score矩阵，在训练过程中，该矩阵中的transition score都会不断地自动更新。也就是说CRF层可以自动学习，通过学习得到一个最优的transition score矩阵，而不用我们手工定义一个transition score矩阵。当模型训练不断地持续，该矩阵会越来越合理。

1.3 CRF损失函数

CRF损失函数中包含了真实标签序列得分和所有可能标签序列的总得分，正常情况下，真实标签序列得分在所有可能标签序列得分中是最高的。

比如，假设数据集中的标签如下所示：

Label	Index
B-Person	0
I-Person	1
B-Organization	2
I-Organization	3
O	4
START	5
END	6

那么，在第一节中我们假设的句子$x$，所有可能的标签序列组合为:

• (1) START B-Person B-Person B-Person B-Person B-Person END
• (2) START B-Person I-Person B-Person B-Person B-Person END
• …
• (10) START B-Person I-Person O B-Organization O END
• …
• (N) O O O O O O O

假设一共有N中可能的标签序列组合，且第$i$个标签序列的得分为$P_i$，那么所有可能标签序列组合的总得分为：

$$P_{total} = P_1 + P_2 + ... + P_N = e^{S_1} + e^{S_2} + ... + e^{S_N}$$

按照我们之前的假设，第10个是真实的标签序列，那么，我们想要的结果是第10个标签序列得分在所有可能的标签序列得分中是最高的。

因此，我们可以定义模型的损失函数，在整个模型训练过程中，BiLSTM-CRF模型的参数不断地进行更新，使得真实标签序列得分在所有可能标签序列组合得分中的占比是最高的。因此，模型的损失函数格式如下所示：

$$LossFunction = \frac{P_{RealPath}}{P_1+P_2+...+P_N}$$

那么，问题就来了：

• 如何定义一个标签序列的得分？
• 如何计算所有可能标签序列组合的总得分？
• 在计算总得分中，一定需要计算每一个可能的标签序列的得分吗？

接下来，我们来解答每一个问题。

1.4 真实标签序列得分

前面我们定义了标签序列得分为$P_i$，以及所有可能标签序列的总得分为：

$$P_{total} = P_1 + P_2 + ... + P_N = e^{S_1} + e^{S_2} + ... + e^{S_N}$$

其中$e^{S_i}$表示第i个标签序列得分。

显然，在所有可能的标签序列组合必然存在一个序列是真实标签序列，而剩下的标签序列组合都是错误的，比如序列”START B-Person I-Person O B-Organization O END “是正确的，而序列‘START B-Person I-Person B-Person B-Person B-Person END’是错误的。

在整个模型训练过程中，CRF层的损失函数只需要两个得分：

• 一个是真实标签序列得分
• 一个是所有可能标签序列组合的总得分

而我们的学习目的是让真实的标签序列得分在总得分中的占比是最高的。

对于真实标签序列的得分$e^{S_i}$，我们直接计算$S_i$即可。

我们使用之前的案例，真实的标签序列为“START B-Person I-Person O B-Organization O END ”，即：

• 句子$x$由5个字符组成，$w_1,w_2,w_3,w_4,w_5$
• 我们在句子前后增加两个字符，记为$w_0,w_6$
• $S_i$主要由第一节中提到的Emission Score和Transition Score组成，即$S_i = Emission Score + Transition Score$

1.4.1 Emission Score

Emission Score计算公式如下所示：

$Emission Score = $

$x_{0,START} + x_{1,B-Person} + x_{2,I-Person} + x_{3,O} +$

$x_{4,B-Organization} + x_{5,O} + x_{6,END}$

其中：

• $x_{index,label}$表示第index个词被标记为label的得分
• $x_{1,B-Person}, x_{2,I-Person} , x_{3,O}, x_{4,B-Organization},x_{5,O}$ 为BiLSTM层的输出
• 一般$x_{0,START}$和$x_{6,END}$为0

1.4.2 Transition Score

Transition Score计算公式如下所示:

$Transition Score =$
$t_{START \rightarrow B-Person} + t_{B-Person \rightarrow I-Person} +$
$t_{I-Person \rightarrow O} + t_{O \rightarrow B-Organization} + t_{B-Organization \rightarrow O} + t_{O \rightarrow END}$

其中:

• $t_{label1 \rightarrow label2}$ 表示$label1$到$label2$的transition Score。
• transition Score主要是在CRF层进行计算的，也就是说，transition Score完全是CRF层的参数。

因此，我们通过计算$s_i$，可以得到第i条标签序列的得分。

1.5 所有可能标签序列组合的总得分

前面，我们计算了单条标签序列得分，接下来，我们需要计算所有可能标签序列的总得分。由之前内容可知，总得分的计算公式为;

$$P_{total} = P_1 + P_2 + ... + P_N = e^{S_1} + e^{S_2} + ... + e^{S_N}$$

很显然，总得分计算方式就是每一条标签序列得分的求和，那么我们能想到的最简单的方法就是先计算每一条的标签序列得分，然后将所有的标签序列得分进行相加得到总得分。虽然计算很简单，但是效率不高，需要很长的训练时间。

接下来,我们将通过公式推导来认识总得分计算过程。

1.6 CRF的损失函数

由前面可知，CRF层的损失函数为:

$$Loss Function = \frac{P_{RealPath}}{P_1 + P_2 + … + P_N}$$

我们对其对数化，即：

$$LogLossFunction = \log \frac{P_{RealPath}}{P_1 + P_2 + … + P_N}$$

一般在模型训练过程中，我们希望损失函数最小化，因此，在损失函数添加一个负号，即:

$Log Loss Function$
$= - \log \frac{P_{RealPath}}{P_1 + P_2 + … + P_N}$
$= - \log \frac{e^{S_{RealPath}}}{e^{S_1} + e^{S_2} + … + e^{S_N}}$
$= - (\log(e^{S_{RealPath}}) - \log(e^{S_1} + e^{S_2} + … + e^{S_N}))$
$= - (S_{RealPath} - \log(e^{S_1} + e^{S_2} + … + e^{S_N}))$
$= - ( \sum_{i=1}^{N} x_{iy_i} + \sum_{i=1}^{N-1} t_{y_iy_{i+1}} - \log(e^{S_1} + e^{S_2} + … + e^{S_N}))$

因此，对于总得分，我们需要一个高效的方法计算:

$$\log(e^{S_1} + e^{S_2} + … + e^{S_N})$$

1.6.1 emission Score和transition Score

为了简化公式，我们假设句子的长度为3，即:

$x = (w_0,w_1,w_2)$

假设数据集中只有两个标签，即：

$LabelSet = (l_1,l_2)$

则emission Score矩阵可从BiLSTM层的输出获得，即：

	$l_1$	$l_2$
$w_0$	$x_{01}$	$x_{02}$
$w_1$	$x_{11}$	$x_{12}$
$w_2$	$x_{21}$	$x_{22}$

其中$x_{ij}$为单元$w_i$被标记为$l_j$的得分。

而且，我们可以从CRF层中得到transition Score矩阵，即:

	$l_1$	$l_2$
$l_1$	$t_{11}$	$t_{12}$
$l_2$	$t_{21}$	$t_{22}$

其中$t_{ij}$为标签$i$到标签$j$的得分。

1.6.2 公式推导

记住我们的目标是计算: $\log(e^{S_1} + e^{S_2} + … + e^{S_N})$

很显然，我们可以使用动态规划思想进行计算（如果你不了解动态规划，没关系，本文将一步一步地进行解释，当然还是建议你学习下动态规划算法）。简而言之，首先，我们计算$w_0$的所有可能序列的总得分。接着，我们使用上一步的总得分计算$w_0 \rightarrow w_1$的总得分。最后，我们同样使用上一步的总得分计算$w_0 \rightarrow w_1 \rightarrow w_2$的总得分。最后的总得分就是我们想要的总得分。

很明显，我们每一次计算都需要利用到上一步计算得到的结果，因此，接下来，你将看到两个变量:

• obs: 定义当前单元的信息
• previous: 存储上一步计算的最后结果

---

备注：以下内容如果看不懂的话，结合上面的emission Score矩阵和transition Score矩阵一起看就明白了

首先，我们计算$w_0$:

$obs = [x_{01},x_{02}]$
$previous = None$

如果我们的句子只有一个词$w_0$，那么存储上一步结果的$previous$为$None$，另外，对于$w_0$而言，$obs = [x_{01},x_{02}]$，其中$x_{01}$和$x_{02}$分别为emission Score（ＢiLSTM层的输出）。

因此，$w_0$的所有可能标签序列总得分为:

$TotalScore(w_0)=\log (e^{x_{01}} + e^{x_{02}})$

---

接着，我们计算$w_0 \rightarrow w_1$:

$obs = [x_{11},x_{12}]$
$previous = [x_{01},x_{02}]$

为了计算方便，我们将$previous$转变为:

$$previous = \begin{pmatrix} x_{01} & x_{01} \\ x_{02} & x_{02} \end{pmatrix}$$

同样，将$obs$转变为:

$$obs = \begin{pmatrix} x_{11} & x_{12} \\ x_{11} & x_{12} \end{pmatrix}$$

备注：通过矩阵方式计算更高效

接着，我们将$previous,abs$和transition Score进行相加,即:

$$scores = \begin{pmatrix} x_{01}&x_{01}\\ x_{02}&x_{02} \end{pmatrix} + \begin{pmatrix} x_{11}&x_{12}\\ x_{11}&x_{12} \end{pmatrix} + \begin{pmatrix} t_{11}&t_{12}\\ t_{21}&t_{22} \end{pmatrix}$$

接着，可得到:

$$scores = \begin{pmatrix} x_{01}+x_{11}+t_{11}&x_{01}+x_{12}+t_{12}\\ x_{02}+x_{11}+t_{21}&x_{02}+x_{12}+t_{22} \end{pmatrix}$$

从而我们可得到当前的$previous$为:

$$previous=[\log (e^{x_{01}+x_{11}+t_{11}} + e^{x_{02}+x_{11}+t_{21}}), \log (e^{x_{01}+x_{12}+t_{12}} + e^{x_{02}+x_{12}+t_{22}})]$$

实际上，第二步已经算完了，可能还有人还无法理解如何得到$w_0$到$w_1$的所有可能序列组合（$label_1 \rightarrow label_1, label_1 \rightarrow label_2 , label_2 \rightarrow label_1, label_2 \rightarrow label_2$）的总得分，其实你主要按照以下计算方式即可;

$TotalScore(w_0 → w_1)$

$=\log (e^{previous[0]} + e^{previous[1]})$

$=\log (e^{\log(e^{x_{01}+x_{11}+t_{11}} + e^{x_{02}+x_{11}+t_{21}})}+
e^{\log(e^{x_{01}+x_{12}+t_{12}} + e^{x_{02}+x_{12}+t_{22}})}
)$

$=\log(e^{x_{01}+x_{11}+t_{11}}+e^{x_{02}+x_{11}+t_{21}}+e^{x_{01}+x_{12}+t_{12}}+e^{x_{02}+x_{12}+t_{22}})$

很明显，与$\log(e^{S_1} + e^{S_2} + … + e^{S_N})$很相似。

在上述公式中，我们可以看到:

• $S_1 = x_{01}+x_{11}+t_{11}$ ($label_1$ → $label_1$)
  • $S_2 = x_{02}+x_{11}+t_{21}$ ($label_2$ → $label_1$)
  • $S_3 = x_{01}+x_{12}+t_{12}$ ($label_1$ → $label_2$)
  • $S_4 = x_{02}+x_{12}+t_{22}$ ($label_2$ → $label_2$)

---

接着我们计算$w_0$ → $w_1$ → $w_2$:

如果你理解了上一步的计算过程的话，其实这一步的计算与上一步类似。即：

$obs = [x_{21}, x_{22}]$

$previous=[\log (e^{x_{01}+x_{11}+t_{11}} + e^{x_{02}+x_{11}+t_{21}}), \log (e^{x_{01}+x_{12}+t_{12}} + e^{x_{02}+x_{12}+t_{22}})]$

类似于第二步，我们将$previous$转化为:

$$previous = \begin{pmatrix} \log (e^{x_{01}+x_{11}+t_{11}} + e^{x_{02}+x_{11}+t_{21}})&\log (e^{x_{01}+x_{11}+t_{11}} + e^{x_{02}+x_{11}+t_{21}})\\ \log (e^{x_{01}+x_{12}+t_{12}} + e^{x_{02}+x_{12}+t_{22}})&\log (e^{x_{01}+x_{12}+t_{12}} + e^{x_{02}+x_{12}+t_{22}}) \end{pmatrix}$$

同样，将$obs$转化为:

$$obs = \begin{pmatrix} x_{21}&x_{22}\\ x_{21}&x_{22} \end{pmatrix}$$

将$previous，obs$和transition Score进行相加，即:

$scores =$
$\begin{pmatrix}
\log (e^{x_{01}+x_{11}+t_{11}} + e^{x_{02}+x_{11}+t_{21}})&\log (e^{x_{01}+x_{11}+t_{11}} + e^{x_{02}+x_{11}+t_{21}})\\
\log (e^{x_{01}+x_{12}+t_{12}} + e^{x_{02}+x_{12}+t_{22}})&\log (e^{x_{01}+x_{12}+t_{12}} + e^{x_{02}+x_{12}+t_{22}})
\end{pmatrix}$
$+$
$\begin{pmatrix}
x_{21}&x_{22}\\
x_{21}&x_{22}
\end{pmatrix}$
$+$
$\begin{pmatrix}
t_{11}&t_{12}\\
t_{21}&t_{22}
\end{pmatrix}$

更新$previous$为:

$previous = [\log(
e^{\log (e^{x_{01}+x_{11}+t_{11}} + e^{x_{02}+x_{11}+t_{21}}) + x_{22} + t_{12}}
+
e^{\log (e^{x_{01}+x_{12}+t_{12}} + e^{x_{02}+x_{12}+t_{22}}) + x_{22} + t_{22}})]$
$=\log( (e^{x_{01}+x_{11}+t_{11}} + e^{x_{02}+x_{11}+t_{21}})e^{x_{22} + t_{12}} + (e^{x_{01}+x_{12}+t_{12}} + e^{x_{02}+x_{12}+t_{22}})e^{x_{22} + t_{22}})]$

当计算到最后一步时，我们使用新的$previous$计算总得分:

$TotalScore(w_0 → w_1 → w_2)$

$=\log (e^{previous[0]} + e^{previous[1]})$

$=\log (e^{\log(
(e^{x_{01}+x_{11}+t_{11}} + e^{x_{02}+x_{11}+t_{21}})e^{x_{21} + t_{11}}
+
(e^{x_{01}+x_{12}+t_{12}} + e^{x_{02}+x_{12}+t_{22}})e^{x_{21} + t_{21}}
)}$

$+e^{\log(
(e^{x_{01}+x_{11}+t_{11}} + e^{x_{02}+x_{11}+t_{21}})e^{x_{22} + t_{12}}
+
(e^{x_{01}+x_{12}+t_{12}} + e^{x_{02}+x_{12}+t_{22}})e^{x_{22} + t_{22}})}
)$

$=\log (e^{x_{01}+x_{11}+t_{11}+x_{21}+t_{11}}+e^{x_{02}+x_{11}+t_{21}+x_{21}+t_{11}}$
$+e^{x_{01}+x_{12}+t_{12}+x_{21}+t_{21}}+e^{x_{02}+x_{12}+t_{22}+x_{21}+t_{21}}$
$+e^{x_{01}+x_{11}+t_{11}+x_{22}+t_{12}}+e^{x_{02}+x_{11}+t_{21}+x_{22}+t_{12}}$
$+e^{x_{01}+x_{12}+t_{12}+x_{22}+t_{22}}+e^{x_{02}+x_{12}+t_{22}+x_{22}+t_{22}})$

---

到这里，我们就完成 了$\log(e^{S_1} + e^{S_2} + … + e^{S_N})$的计算过程。

参考文献

[1] Lample, G., Ballesteros, M., Subramanian, S., Kawakami, K. and Dyer, C., 2016. Neural architectures for named entity recognition. arXiv preprint arXiv:1603.01360.
https://arxiv.org/abs/1603.01360