FM算法-python实现

我仍然记得第一次遇到点击率预测问题时的情形，在那之前，我一直在学习数据科学，对自己取得的进展很满意，在机器学习黑客马拉松活动中也开始建立了自信，并决定好好迎接不同的挑战。

为了做得更好，我购买了一台内存16GB，i7处理器的机器，但是当我看到数据集的时候却感到非常不安，解压缩之后的数据大概有50GB - 我不知道基于这样的数据集要怎样进行点击率预测。幸运地是，Factorization Machines(FM)算法拯救了我。

任何从事点击率预测问题或者推荐系统相关工作的人都会遇到类似的情况。由于数据量巨大，利用有限的计算资源对这些数据集进行预测是很有挑战性的。

然而在大多数情况下，由于很多特征对预测并不重要，所以这些数据集是稀疏的（每个训练样本只有几个变量是非零的）。在数据稀疏的场景下，因子分解有助于从原始数据中提取到重要的潜式或隐式的特征。

因子分解有助于使用低维稠密矩阵来表示目标和预测变量之间的近似关系。在本文中我将讨论算法Factorization Machines(FM) 和Field-Aware Factorization Machines(FFM)，然后在回归/分类问题中讨论因子分解的优势，并通过python编程实现。

因子分解的直观介绍

为了直观地理解矩阵分解，我们来看一个例子：假设有一个用户-电影评分（1-5）矩阵，矩阵中的每一个值表示用户给电影的评分（1-5）。

	Star Wars I	Inception	Godfather	The Notebook
u1	5	3	-	1
u2	4	-	-	1
u3	1	1	-	5
u4	1	-	-	4
u5	-	1	5	4

从上述表格中我们可以看出，一些评分是缺失的，我们想设计一种方法来预测这些缺失的评分。直观上来讲，利用矩阵分解来解决这个问题的关键是应该有一些潜在的特征决定用户如何评价一部电影。举例来说 - 用户A和B都是演员阿尔·帕西诺的粉丝，那么他们就会对阿尔·帕西诺的电影评分较高。在上述例子中，对特定演员的偏好是一个隐藏的特性，因为我们没有明确地将其包含在评分矩阵中。

假设我们要计算K个隐藏或潜在的特征，我们的任务是找出矩阵P (U x K)和Q (D x K) (U – 用户, D – 电影)，使得 P x QT 近似等于评分矩阵R。

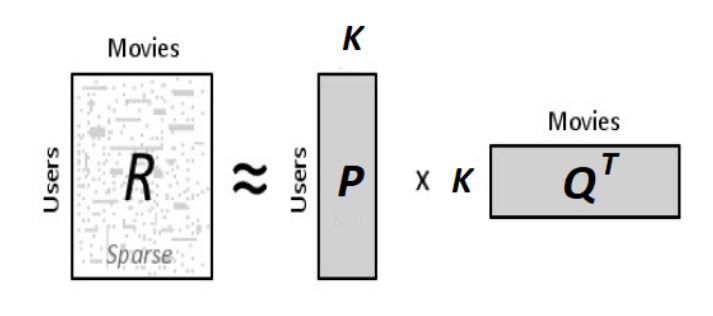
P矩阵的每一行表示用户与不同特征的相关性，Q矩阵的每一行表示该特征与电影同样的相关性。为了得到用户ui对电影dj的评分，我们可以计算对应于ui和dj两个向量的点积。

$$r_{ij} = p_{i}^T q_{j}$$

接下来要做的就是求出矩阵P和矩阵Q。我们使用梯度下降算法来计算，目标函数是使用户的实际评分与通过矩阵P和Q估计的评分之间的平方误差最小，这里的平方误差由以下方程求出。

$$e^2_{ij} = (r_{ij} - \hat{r_{ij}})^2 = (r_{ij} - \sum_{k=1}^{K}p_{ik}q_{kj})^2$$

现在我们要给pik和qkj定义一个更新规则，梯度下降法中的更新规则是由最小化误差值的梯度来定义的。

$$\frac{\partial}{\partial p_{ik}} e_{ij}^2 = -2(r_{ij} - \hat{r}_{ij})(q_{kj}) = -2e_{ij}q_{kj}$$

$$\frac{\partial}{\partial q_{kj}} e_{ij}^2 = -2(r_{ij} - \hat{r}_{ij})(p_{ik}) = -2e_{ij}p_{ik}$$

获得梯度值后，接下来可以定义$p_{ik}$和$q_{kj}$的更新规则。

$$p^{'}_{ik} = p_{ik} +\alpha \frac{\partial}{\partial p_{ik}} e^2_{ij} = p_{Ik} + 2\alpha e_{ij}q_{kj}$$

$$q^{'}_{kj} = q_{kj} +\alpha \frac{\partial}{\partial q_{kj}} e^2_{ij} = q_{kj}+ 2\alpha e_{ij}p_{ik}$$

其中α是控制更新步长的学习速率，使用上述更新规则，我们可以迭代地执行操作，直到误差收敛到最小，同时使用下面的公式计算总的误差，以此来确定什么情况下应该停止迭代。

$$E = \sum_{(u_i,d_j,r_{ij}) \in T } e_{ij} = \sum_{(u_i,d_j,r_{ij}) \in T} (r_{ij} - \sum_{k=1}^K p_{ik}q_{kj})^2$$

上述解决方案很简单并且经常会导致过拟合，即现有的评分都被准确预测到，但是不能很好地推广到未知的数据上。为了解决这个问题，我们可以引入一个正则化参数 β，它将分别控制矩阵P和Q中向量“用户-特征”和“电影-特征”，并给出一个更好的评分的近似值。

使用python实现上述功能:

#encoding:utf-8
import numpy as np

"""
@INPUT:
    R     : a matrix to be factorized, dimension N x M
    P     : an initial matrix of dimension N x K
    Q     : an initial matrix of dimension M x K
    K     : the number of latent features
    steps : the maximum number of steps to perform the optimisation
    alpha : the learning rate
    beta  : the regularization parameter
@OUTPUT:
    the final matrices P and Q
"""
def matrix_factorization(R,P,Q,K,steps = 5000,alpha = 0.0002,beta =0.02):
    Q = Q.T
    for step in range(steps):
        for i in range(len(R)):
            for j in range(len(R[i])):
                if R[i][j] >0 :
                    e_ij = R[i][j] - np.dot(P[i,:],Q[:,j])
                    for k in range(K):
                        P[i][k] = P[i][k] + alpha * (2 * e_ij * Q[k][j] - beta * P[i][k])
                        Q[k][j] = Q[k][j] + alpha * (2 * e_ij * P[i][k] - beta * Q[k][j])
        e = 0
        for i in xrange(len(R)):
            for j in xrange(len(R[i])):
                if R[i][j] > 0:
                    e = e + pow(R[i][j] - np.dot(P[i,:],Q[:,j]),2)
                    for k in xrange(K):
                        e = e+ (beta / 2) * (pow(P[i][k],2) + pow(Q[k][j],2))
        if e < 0.001:
            break
    return P,Q.T
if __name__ == "__main__":
    R = [
         [5,3,0,1],
         [4,0,0,1],
         [1,1,0,5],
         [1,0,0,4],
         [0,1,5,4],
        ]
    R = np.array(R)
    N = len(R)
    M = len(R[0])
    K = 2
    P = np.random.rand(N,K)
    Q = np.random.rand(M,K)
    nP, nQ = matrix_factorization(R, P, Q, K)
    print nP
    print nQ

一旦我们用上述方法计算出了矩阵P和Q，得到的近似评分矩阵如下：

	Star Wars I	Inception	Godfather	The Notebook
u1	4.97	2.98	2.18	0.98
u2	3.97	2.4	1.97	0.99
u3	1.02	0.93	5.32	4.93
u4	1.00	0.85	4.59	3.93
u5	1.36	1.07	4.89	4.12

现在，我们既能够重新生成现有评分，也能对未知的评分进行一个合理的近似。

FM算法如何优于多项式和线性模型

首先考虑一组点击率预测数据的训练示例。以下数据来自相关体育新闻网站（发布商）和体育用品公司（广告商）。

Clicked	Publisher	Advertiser	Gender
Yes	ESPN	Nike	Male
No	NBC	Adidas	Male

当我们讨论FM或者FFM的时候，数据集中的每一列（比如上述表格中的出版商、广告商等）将被称为一个字段，每一个值（ ESPN、Nike 等）都被称为一个特征。

线性或逻辑回归模型在很多问题上表现很好，但缺点是这种模型只能学习所有变量或者特征各自的影响，无法学习变量之间的相互作用。

$$\phi LM = w_0 + w_{ES}x_{ES} + w_{Ni}x_{Ni} + w_{Ad}x_{Ad} + w_{NB}x_{NB} + w_{Ma} x_{Ma}$$

在上述等式中，w0、wESPN等代表参数，xESPN、xNike等代表数据集中的各个特征，通过最小化上述函数的对数损失，得到逻辑回归模型。捕获特征之间相互作用的一种方法是使用多项式函数，将每个特征对的乘积作为单独的参数来学习，并且把每一个乘积作为一个独立的变量。

$$\phi poly2 = w_0 + w_{ES}x_{ES} + w_{Ni}x_{Ni} + w_{Ad}x_{Ad} + w_{NB}x_{NB}$$

$$+ w_{Ma} x_{Ma} +w_{ES,Ni}x_{ES,Ni} + w_{ES,Ma} x_{ES,Ma} .........$$

这也可以称为 Poly2模型，因为每一项都只考虑了两个特征之间的相互影响。

• 问题在于，即使面对一个中等大小的数据集，也需要一个庞大的模型，这对存储模型所需要的内存空间和训练模型所花费的时间都有很大的影响

• 其次，对于一个稀疏数据集，这种技术不能很好地学习所有的权重或参数，因为没有有足够的训练样本使每一个特征对的权重是可靠的。

FM

FM算法解决了成对特征交互的问题。它使我们能够根据每一对特征组合中的可靠信息（隐藏特征）来训练模型，同时在时间和空间复杂度上更有效地实现上述目标。具体来讲，它将成对交互特征作为低维向量的点积（长度为K）进行建模，以下包含了一个二阶因子分解的方程。

$$\phi FM = w_0 + w_{ES} x_{ES} + w_{Ni} x_{Ni} + w_{Ma}x_{Ma} + w_{NB}x_{NB} +\sum <v_{j1},v_{j2}>x_{j1}x_{j2}$$

FM（K=3）项中每个参数的表示方法如下：

$$<v_{ES},v_{Ni}> = v_{ES,1} x V_{Ni,1} + v_{ES,2} x v_{Ni,2} + v_{ES,3} x v_{Ni,3} ​$$

上述等式中，我们分别计算了与2个特征对应的2个长度为3的潜因子的点积。

从建模的角度来看，这是非常强大的，因为每一个特征最后都会转换到一个相似特征被互相嵌套的空间，简而言之，点积基本上表示了潜在特征的相似程度，特征越相近，点积越大。

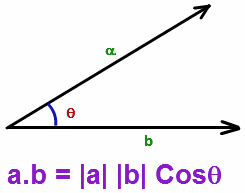
对于余弦函数，当 θ是0时，得到最大值1；当 θ是180度，得到-1，所以当 θ接近于0时，相似性最大。

FM算法的另一个巨大优势是能够在线性时间复杂度下使用简单的数学方法计算模型中成对特征的相互作用。如果你想进一步了解具体的实现步骤，请参考链接中关于FM算法的原始研究论文，请点击论文

示例：FM算法性能优于 POLY2算法的演示

考虑以下一组虚构的点击率数据：

Clicks	Unclicks	Publisher	Adertiser
+80	-20	ESPN	Nike
+10	-90	ESPN	Gucci
+0	-1	ESPN	Adidas
+15	-85	Vogue	Nike
+90	-10	Vogue	Gucci
+10	-90	Vogue	Adidas
+85	-15	NBC	Nike
+0	-0	NBC	Gucci
+90	-10	NBC	Adidas

这个数据集由作为发布者的体育网站和体育用品广告商构成。广告是以弹出的方式来显示的，用户可以选择点击广告或者关闭广告。

• 特征对(ESPN，Adidas)只有一个负的训练数据，那么在Poly2算法中，这个特征对可能会学到一个负的权重值wESPN，Adidas；而在FM算法中，由于特征对(ESPN，Adidas)是由wESPN· wAdidas决定的，而其中的wESPN和wAdidas分别是从其他特征对中学到的（比如(ESPN，Nike)，(NBC，Adidas)等），所以预测可能更加精确。

• 另一个例子是特征对(NBC，Gucci)没有任何训练数据，对于Poly2算法，这个特征对的预测值为0；但是在FM算法中，因为wNBC和wGucci可以从其他特征对中学到，所以仍然有可能得到有意义的预测值。

FFM

Clicked	Publisher	Advertisor	Gender
yes	ESPN	Nike	Male

为了理解FFM算法，我们需要认识field的概念。field通常是指包含一个特定特征的更广泛的类别。在上述训练示例中，field分别指Publisher（P）、Advertisor（A）和Gender（G）。

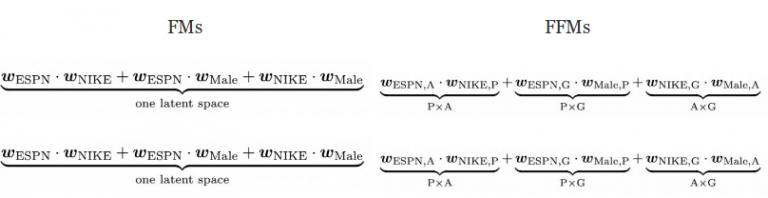
• 在FM算法中，每一个特征只有一个隐向量v，来学习其他特征带来的潜在影响。以ESPN为例，wESPN被用来学习特征Nike(wESPN·wNike)和Male(wESPN.wMale)之间的潜在作用。

• 但是，由于ESPN和Male属于不同的field,所以对特征对(ESPN，Nike)和(ESPN，Male)的起作用的潜在作用可能不同。FM算法无法捕捉这个差异，因为它不区分field的概念，在这两种情况中，它会使用相同参数的点积来计算.

• 在FFM算法中，每个特征有若干个隐向量。例如，当考虑特征ESPN和Nike之间的交互作用时，用符号$w_{ESPN,A}$来表示ESPN的隐藏特征，其中A（Advertisor）表示特征Nike的field。类似的，关于性别的field的一个重要的参数$w_{ESPN,G}也会被学习到。

事实证明，FFM算法对获得由 Criteo、Avazu、Outbrain举办的点击率（CTR）比赛第一名是至关重要的，同时也帮助赢得了2015年RecSys挑战赛的三等奖。关于点击率数据集可以从Kaggle获得。

在python中使用xLearn库进行算法实现

一些在python中实现FM & FFM的最流行的库如下所示：

Package Name	Description
LibFM	FM算法作者提供的一个模块
LibFFM	FFM的扩展
xLearn	包含FM和FFM
tffm	tensorflow实现

为了在数据集上使用FM算法，需要将数据转换为libSVM格式。以下为训练和测试的数据文件格式：

: : …

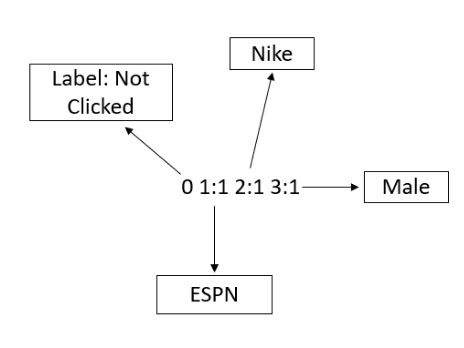
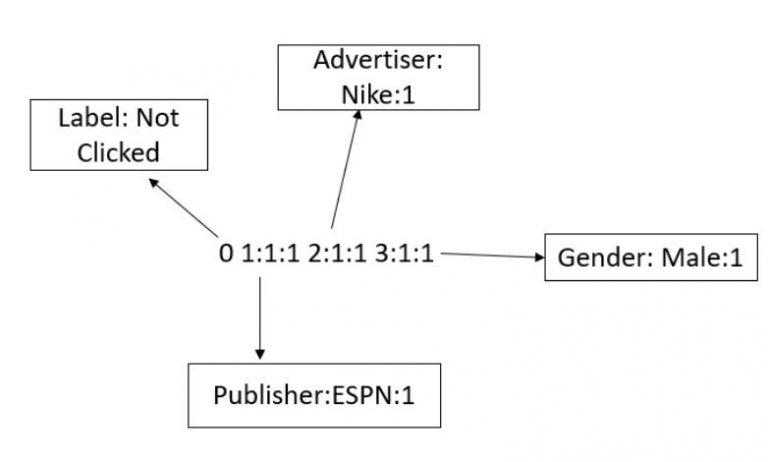
在增加了field的概念之后，每个特征被唯一编码并被赋值，上述图中，特征ESPN用1表示，特征Nike用2表示，以此类推。每一行包含一个等效的训练示例并以“\ n”或换行符结尾。

• 对于分类（二进制/多类），是一个指示类标签的整数。

• 对于回归，是任何实数的目标值。

• 测试文件中的标签仅用于计算准确度或误差，未知的情况下可以用任何数值填写第一列。

同样，对于FFM算法，需要将数据转换为libffm格式。在这里，我们也需要对field进行编码，因为该算法需要field的信息来学习。格式如下：

:::: …

有关数值特征的重要说明

数值特征需要被离散化（通过将特定数值特征的整个范围分成较小的范围并且分别对每个范围进行标记编码而转换为分类特征），然后如上所示转换为libffm格式。

另一种可能性是添加一个与特征值相同的虚拟field值，它将是该特定行的数值特征（例如，具有值45.3的特征可以被变换为1：1：45.3）。 但是虚拟field值可能不包含任何信息，因为它们仅仅是这些数值特征的复制品。

xLearn

最近推出的xLearn库提供了一个在各种数据集上实现FM和FFM模型的快速解决方案。 它比libfm和libffm库快得多，为模型测试和调优提供了更好的功能。

在这里，我们将用一个例子来说明FFM算法，数据来自Criteo点击率预测挑战赛中CTR数据集的一个微小（1％）抽样。 你可以从这里[Office1] 下载这个数据集。

但首先我们需要将其转换为xLearn所需的libffm格式以拟合模型。 以下函数将标准数据帧格式的数据集转换为libffm格式。

#encoding:utf-8
'''
将df转化为libsvm格式
# kernel: https://www.kaggle.com/scirpus/libffm-generator-lb-280
df = Dataframe to be converted to ffm format
Type = Train/Test/Val
Numerics = list of all numeric fields
Categories = list of all categorical fields
Features = list of all features except the Label and Id

'''

def convert_to_ffm(df,type,numerics,categories,features):
    currecntcode = len(numerics)
    catdict = {}
    catcodes = {}
    for x in numerics:
        catdict[x] = 0
    for x in categories:
        catdict[x] = 1
    nrows = df.shape[0]
    ncolumns = len(features)
    with open(str(type) + "_ffm.txt",'w') as text_file:
        # Looping over rows to convert each row to libffm format
        for n,r in enumerate(range(nrows)):
            datastring = ''
            datarow = df.iloc[r].to_dict()
            datastring += str(int(datarow['Label']))
            # For numerical fields, we are creating a dummy field here
            for i,x in enumerate(catdict.keys()):
                if catdict[x] == 0:
                    datastring = datastring +" " +str(i)+":"+str(i)+":"+str(datarow[x])

                else:
                    # For a new field appearing in a training example
                    if x not in catcodes:
                        catcodes[x] = {}
                        currecntcode += 1
                        catcodes[x][datarow[x]] = currecntcode #encoding the feature
                    # For already encoded fields
                    elif datarow[x] not in catcodes[x]:
                        currecntcode += 1
                        catcodes[x][datarow[x]] = currecntcode #encoding the feature
                    code = catcodes[x][datarow[x]]
                    datastring = datastring +" " +str(i) +":"+str(int(code)) +":1"
            datastring += '\n'
            text_file.write(datastring)

xLearn可以直接处理csv以及libsvm格式的数据来实现FM算法，但对FFM算法而言，我们必须将数据转换为libffm格式。

0 0:194689:1 1:219069:1 2:319325:1 3:754755:1 4:515702:1 5:359746:1 6:707332:1 7:396128:1 8:650556:1 9:530364:1 10:148557:1 11:548643:1 12:790331:1 13:344176:1 14:145710:1 15:299224:1 16:901863:1 17:66695:1 18:182671:1 19:832740:1 20:869462:1 21:198788:1 22:660059:1 23:134912:1 24:430579:1 25:285442:1 26:78061:1 27:660466:1 28:326359:1 29:633290:1 30:271271:1 31:765122:1 32:322020:1 33:943765:1 34:541960:1 35:821014:1 36:428618:1 37:607936:1 38:142693:1
0 0:40189:1 1:164503:1 2:659433:1 3:100700:1 4:224808:1 5:463263:1 6:608573:1 7:223864:1 8:169525:1 9:255381:1 10:756430:1 11:832677:1 12:429274:1 13:370671:1 14:226100:1 15:98199:1 16:218827:1 17:397270:1 18:316115:1 19:561396:1 20:50216:1 21:198788:1 22:693070:1 23:859765:1 24:811335:1 25:812374:1 26:198506:1 27:581745:1 28:809536:1 29:166818:1 30:642460:1 31:998174:1 32:614600:1 33:34050:1 34:541960:1 35:543189:1 36:101169:1 37:335222:1 38:975766:1

一旦我们有了libffm格式的数据集，就可以使用xLearn库来训练模型。

类似于任何其他机器学习算法，数据集被分成一个训练集和一个验证集。xLearn使用验证/测试对数损失来自动执行提前停止的操作，并且我们还可以在随机梯度下降的迭代中为验证集设置其他的监控指标。

下面的python脚本可以用于在ffm格式的数据集上使用xLearn来训练和调整FFM模型的超参数。

xlearn安装时候需要提前安装CMake模块pip install CMake，然后在使用命令pip install xlearn

import xlearn as xl
ffm_model = xl.create_ffm()
ffm_model.setTrain('criteo.tr.r100.gbdt0.ffm') # 加载数据
ffm_model.setValidate('criteo.va.r100.gbdt0.ffm')
# 参数
param = {"task":'binary', # ‘binary’ for classification, ‘reg’ for Regression
         'k':2,    # Size of latent factor
         'lr':0.1, # Learning rate for GD
         'lambda':0.0002, # L2 Regularization Parameter
         'metric':'auc', # Metric for monitoring validation set performance
         'epoch':25     # Maximum number of Epochs
         }
# 训练模型
ffm_model.fit(param,'model.out')

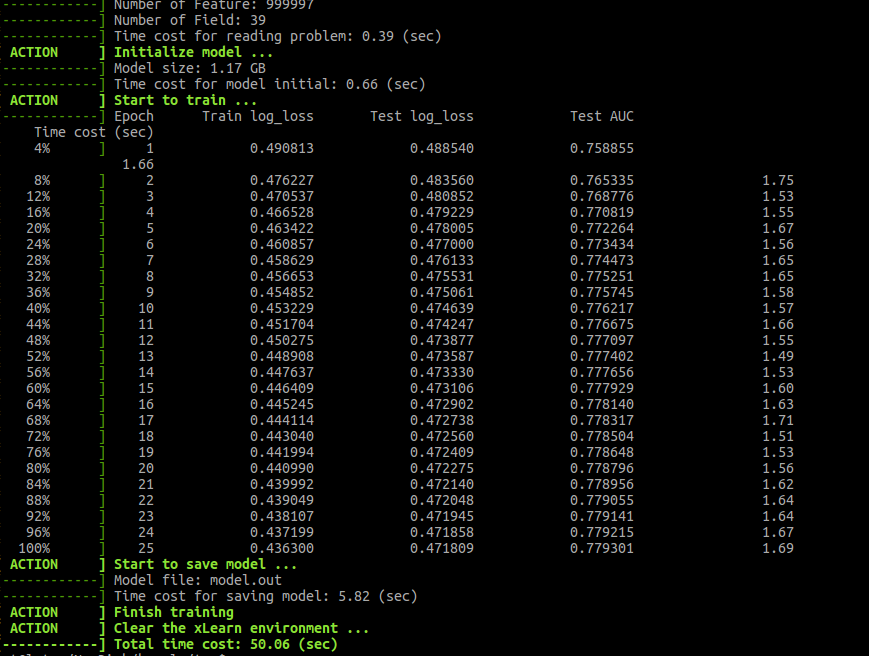
该库还允许我们使用cv()函数进行交叉验证：

ffm_model.cv(param)

默认是5折交叉验证

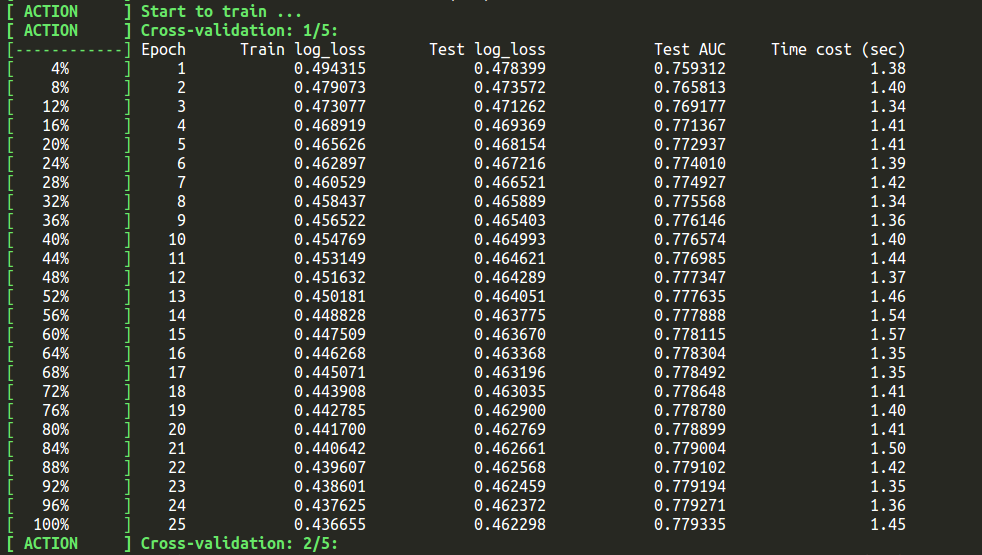
可以使用以下代码片段对测试集进行预测：

# Convert output to 0/1
ffm_model.setTest("criteo.va.r100.gbdt0.ffm")
ffm_model.setSigmoid()
ffm_model.predict("model.out", "output.txt")

结语

在这篇文章中，我们已经演示了对一般分类/回归问题的因式分解的用法。如果您在执行这个算法的过程中遇到任何问题请及时告知我们。有关xLearn详细文档将在这个链接中给出，并会得到定期更新和支持。

原文地址： https://www.analyticsvidhya.com/blog/2018/01/factorization-machines/