在机器学习或者深度学习实验中,我们通常使用大量的正则化技术,比如L1,L2,Dropout等来防止模型发生过拟合问题,在分类问题中,模型往往可以正确的预测训练样本,但是泛化能力比较弱,本文将讨论作为分类问题经常使用的正则化技术–标签平滑。
方法
假设有一个分类模型,预测观测样本x x x K K K x x x q θ ( y ∣ x ) q_{\theta}(y|x) q θ ( y ∣ x ) x x x ∑ y = 1 K q θ ( y ∣ x i ) = 1 \sum_{y=1}^K q_{\theta}(y|x_i)=1 ∑ y = 1 K q θ ( y ∣ x i ) = 1 θ \theta θ p ( y ∣ x ) p(y|x) p ( y ∣ x ) y y y ∑ y = 1 K p ( y ∣ x i ) = 1 \sum_{y=1}^K p(y|x_i)=1 ∑ y = 1 K p ( y ∣ x i ) = 1
通常进行分类任务时,我们采用交叉熵损失函数,使模型预测的概率分布q θ ( y ∣ x ) q_{\theta}(y|x) q θ ( y ∣ x ) p ( y ∣ x ) p(y|x) p ( y ∣ x )
H i ( p , q θ ) = − ∑ y = 1 K p ( y ∣ x i ) log q θ ( y ∣ x i ) \begin{aligned}
H_{i}(p,q_{\theta}) &= - \sum_{y=1}^{K} p(y|x_i) \log q_{\theta}(y|x_i) \\
\end{aligned}
H i ( p , q θ ) = − y = 1 ∑ K p ( y ∣ x i ) log q θ ( y ∣ x i )
则得到的交叉熵损失函数为;
L = ∑ i = 1 n H i ( p , q θ ) = − ∑ i = 1 n ∑ y = 1 K p ( y ∣ x i ) log q θ ( y ∣ x i ) \begin{aligned}
L &= \sum_{i=1}^{n} H_i(p,q_{\theta}) \\
&= - \sum_{i=1}^{n} \sum_{y=1}^{K} p(y|x_i) \log q_{\theta}(y|x_i) \\
\end{aligned}
L = i = 1 ∑ n H i ( p , q θ ) = − i = 1 ∑ n y = 1 ∑ K p ( y ∣ x i ) log q θ ( y ∣ x i )
通过上面公式,可以很轻松的得到样本的损失。
one-hot编码
在进行模型训练时,通常采用类似one-hot编码的0或1的方式对真实分布p ( y ∣ x ) p(y|x) p ( y ∣ x ) p ( y ∣ x ) p(y|x) p ( y ∣ x )
p ( y ∣ x i ) = { 1 if y = y i 0 otherwise p(y|x_i) =
\begin{cases}
1 & \text{if } y = y_i \\
0 & \text{otherwise}
\end{cases}
p ( y ∣ x i ) = { 1 0 if y = y i otherwise
则对应的交叉熵损失函数为:
L = ∑ i = 1 n H i ( p , q θ ) = − ∑ i = 1 n ∑ y = 1 K p ( y ∣ x i ) log q θ ( y ∣ x i ) = − ∑ i = 1 n p ( y i ∣ x i ) log q θ ( y i ∣ x i ) = − ∑ i = 1 n log q θ ( y i ∣ x i ) \begin{aligned}
L &= \sum_{i=1}^{n} H_i(p,q_{\theta}) \\
&= - \sum_{i=1}^{n} \sum_{y=1}^{K} p(y|x_i) \log q_{\theta}(y|x_i) \\
&= - \sum_{i=1}^{n} p(y_i|x_i) \log q_{\theta}(y_i|x_i) \\
&= - \sum_{i=1}^{n} \log q_{\theta}(y_i|x_i) \\
\end{aligned}
L = i = 1 ∑ n H i ( p , q θ ) = − i = 1 ∑ n y = 1 ∑ K p ( y ∣ x i ) log q θ ( y ∣ x i ) = − i = 1 ∑ n p ( y i ∣ x i ) log q θ ( y i ∣ x i ) = − i = 1 ∑ n log q θ ( y i ∣ x i )
从上面的损失函数可以发现计算的损失只考虑正确标签位置的损失,而不考虑其他标签位置的损失,这就会出现一个问题,即不考虑其他错误标签位置的损失,这会使得模型过于关注增大预测正确标签的概率,而不关注减少预测错误标签的概率,最后导致的结果是模型在自己的训练集上拟合效果非常良好,而在其他的测试集结果表现不好,即过拟合,也就是说模型泛化能力差。
另一方面,在优化过程中,如果使用softmax 分类器,即。
q θ ( y i ∣ x i ) = exp ( z y i ) ∑ j = 1 K exp ( z j ) q_{\theta}(y_i|x_i) = \frac{\exp(z_{y_i})}{\sum_{j=1}^{K}\exp(z_j)}
q θ ( y i ∣ x i ) = ∑ j = 1 K exp ( z j ) exp ( z y i )
那么,最小化损失函数会使得正确类和其它类的权重差异变得很大。根据softmax 函数的性质可知,如果要使得某一类的输出概率接近于1,其未归一化的得分需要远大于其它类的得分,可能会导致其权重越来越大,并导致过拟合。
因此,总的来说,对于损失函数,我们需要用预测概率去拟合真实概率,而拟合one-hot的真实概率函数会带来两个问题:
无法保证模型的泛化能力,容易造成过拟合。
全概率和0概率鼓励所属类别和其他类别之间的差距尽可能加大,而由梯度有界可知,这种情况很难适应。会造成模型过于相信预测的类别。
那么,我们如何确保在训练过程中,模型不会对训练数据的标签过度高置信度预测?如果使用one-hot编码标签,过拟合似乎是不可避免的,因此,引入了另一种正则化技术-标签平滑。
label smoothing
为了改善上述情况,我们可以引入一个噪声对标签进行平滑,即假设样本以ϵ 的概率为其它类,即:
p ′ ( y ∣ x i ) = ( 1 − ε ) p ( y ∣ x i ) + ε u ( y ∣ x i ) = { 1 − ε + ε u ( y ∣ x i ) if y = y i ε u ( y ∣ x i ) otherwise \begin{aligned}
p^{\prime}(y|x_i) &= (1-\varepsilon) p(y|x_i) + \varepsilon u(y|x_i) \\
&=
\begin{cases}
1 - \varepsilon + \varepsilon u(y|x_i) & \text{if } y = y_i \\
\varepsilon u(y|x_i) & \text{otherwise}
\end{cases}
\end{aligned}
p ′ ( y ∣ x i ) = ( 1 − ε ) p ( y ∣ x i ) + ε u ( y ∣ x i ) = { 1 − ε + ε u ( y ∣ x i ) ε u ( y ∣ x i ) if y = y i otherwise
其中,在实际应用过程中,u ( y ∣ x ) u(y|x) u ( y ∣ x )
u ( y ∣ x ) = 1 K u(y|x) = \frac{1}{K}
u ( y ∣ x ) = K 1
备注 :如果u ( y ∣ x ) u(y|x) u ( y ∣ x )
接下来,使用的新的分布计算交叉熵损失,即:
L ′ = − ∑ i = 1 n ∑ y = 1 K p ′ ( y ∣ x i ) log q θ ( y ∣ x i ) = − ∑ i = 1 n ∑ y = 1 K [ ( 1 − ε ) p ( y ∣ x i ) + ε u ( y ∣ x i ) ] log q θ ( y ∣ x i ) \begin{aligned}
L^{\prime} &= - \sum_{i=1}^{n} \sum_{y=1}^{K} p^{\prime}(y|x_i) \log q_{\theta}(y|x_i) \\
&= - \sum_{i=1}^{n} \sum_{y=1}^{K} \big[ (1-\varepsilon) p(y|x_i) + \varepsilon u(y|x_i) \big] \log q_{\theta}(y|x_i) \\
\end{aligned}
L ′ = − i = 1 ∑ n y = 1 ∑ K p ′ ( y ∣ x i ) log q θ ( y ∣ x i ) = − i = 1 ∑ n y = 1 ∑ K [ ( 1 − ε ) p ( y ∣ x i ) + ε u ( y ∣ x i ) ] log q θ ( y ∣ x i )
进一步可得到损失函数为:
L ′ = ∑ i = 1 n { ( 1 − ε ) [ − ∑ y = 1 K p ( y ∣ x i ) log q θ ( y ∣ x i ) ] + ε [ − ∑ y = 1 K u ( y ∣ x i ) log q θ ( y ∣ x i ) ] } = − ∑ i = 1 n [ ( 1 − ε ) H i ( p , q θ ) + ε H i ( u , q θ ) ] \begin{aligned}
L^{\prime} &= \sum_{i=1}^{n} \bigg\{ (1-\varepsilon) \Big[ - \sum_{y=1}^{K} p(y|x_i) \log q_{\theta}(y|x_i) \Big] + \varepsilon \Big[ - \sum_{y=1}^{K} u(y|x_i) \log q_{\theta}(y|x_i) \Big] \bigg\} \\
&= - \sum_{i=1}^{n} \Big[ (1-\varepsilon) H_i(p,q_{\theta}) + \varepsilon H_i(u,q_{\theta}) \Big] \\
\end{aligned}
L ′ = i = 1 ∑ n { ( 1 − ε ) [ − y = 1 ∑ K p ( y ∣ x i ) log q θ ( y ∣ x i ) ] + ε [ − y = 1 ∑ K u ( y ∣ x i ) log q θ ( y ∣ x i ) ] } = − i = 1 ∑ n [ ( 1 − ε ) H i ( p , q θ ) + ε H i ( u , q θ ) ]
关于更详细的标签平滑信息,可以看paper: When Does Label Smoothing Help?
实验
接下里,我们将对CIFAR-10数据进行实验,模型主要使用ResNet18,
定义一个标签平滑交叉熵损失:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import torch.nn as nnimport torch.nn.functional as Fclass LabelSmoothingCrossEntropy (nn.Module): def __init__ (self, eps=0.1 , reduction='mean' ): super (LabelSmoothingCrossEntropy, self ).__init__() self .eps = eps self .reduction = reduction def forward (self, output, target ): c = output.size()[-1 ] log_preds = F.log_softmax(output, dim=-1 ) if self .reduction=='sum' : loss = -log_preds.sum () else : loss = -log_preds.sum (dim=-1 ) if self .reduction=='mean' : loss = loss.mean() return loss*self .eps/c + (1 -self .eps) * F.nll_loss(log_preds, target, reduction=self .reduction)
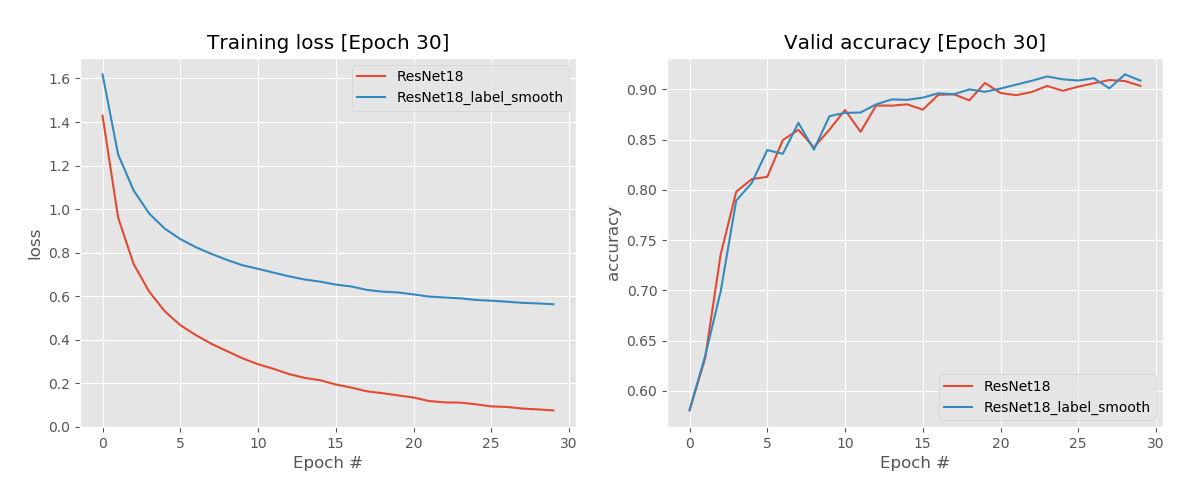
实验结果如下:
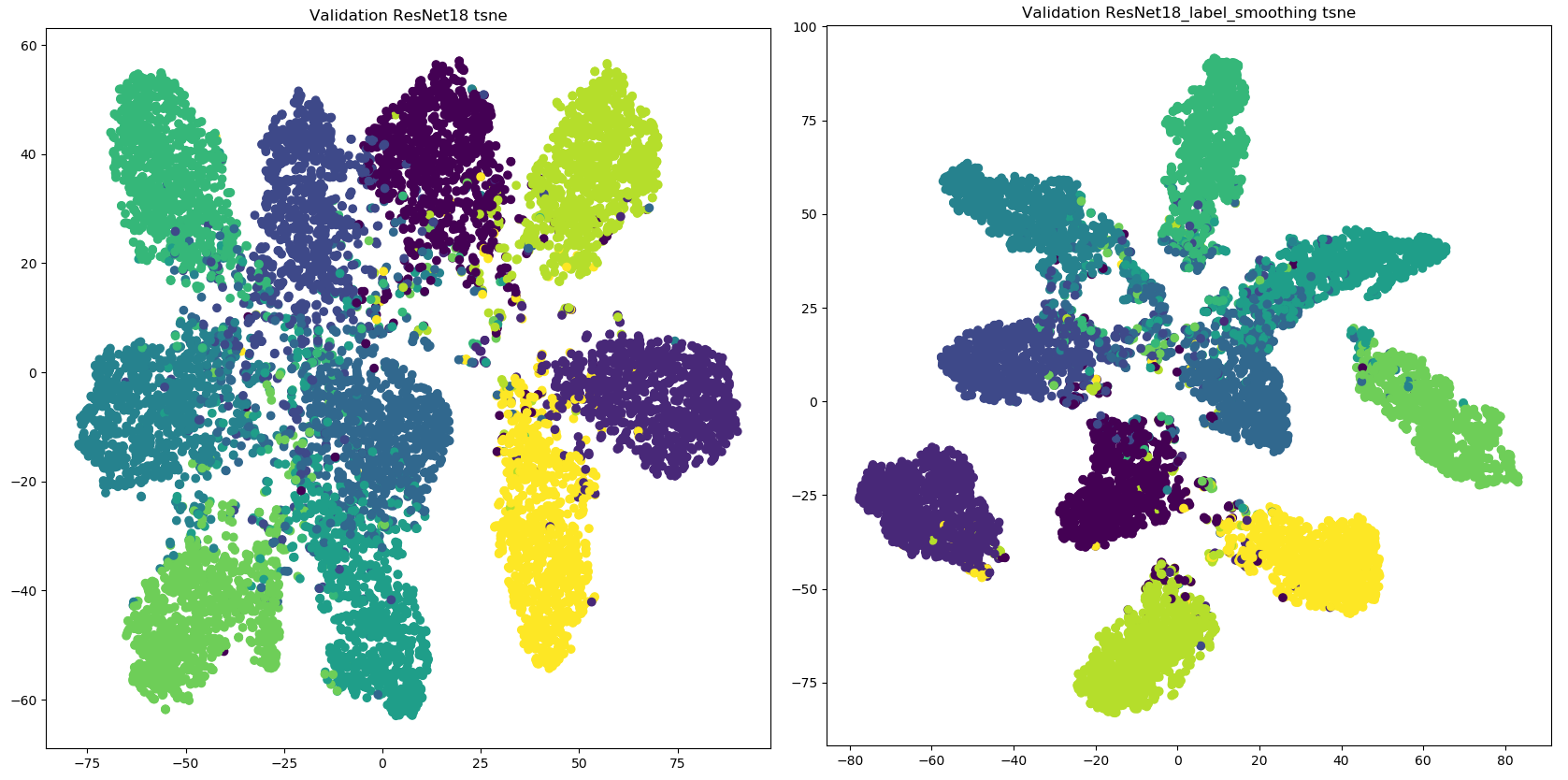
正如图像所显示的,标签平滑为最终的激活产生了更紧密的聚类和更大的类别间的分离。
这是为什么标签平滑可以产生更多的正则化和鲁棒的神经网络的主要原因,重要的是趋向于更好地泛化未来的数据。然而,除了得到了更好的激活值的中心,还有额外的好处。
完整代码地址: https://github.com/lonePatient/label_smoothing_pytorch