我们知道学习率是深度学习模型中一个非常重要的超参数,因此,当训练深度学习模型时,我们如何确定学习率的大小? 如果学习率太小,网络将会训练很慢且耗时(比如学习率设置为1e-6)。如果学习率太高,网络在训练过程中可能会跳过最小值点。更糟糕的是,高学习率可能会导致loss不断变大,这样就脱离了模型的学习目标。
介绍
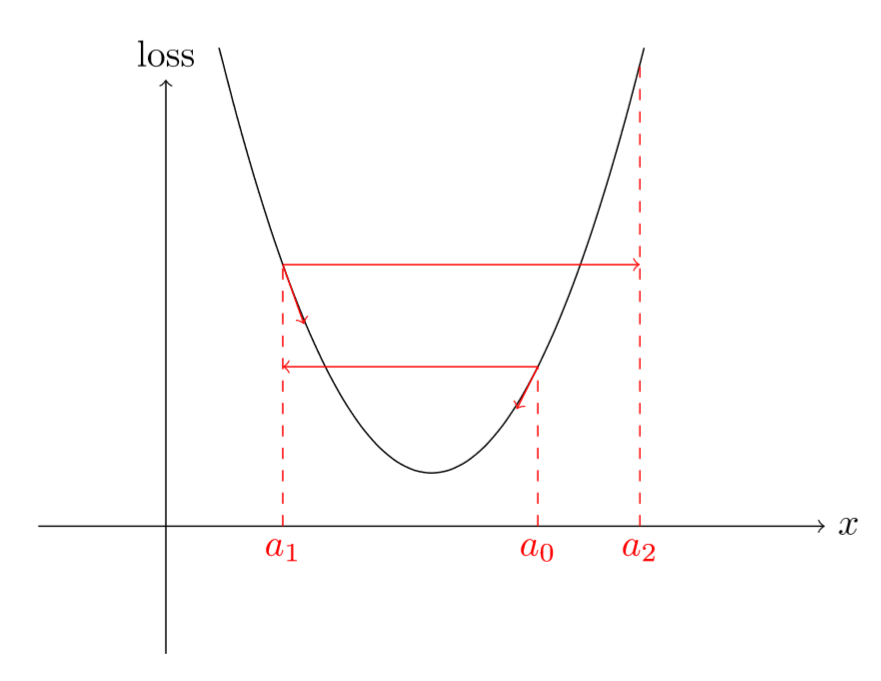
如下图所示,高的学习率,可能会出现跳过最小值点情况,并且loss还增加:
图1
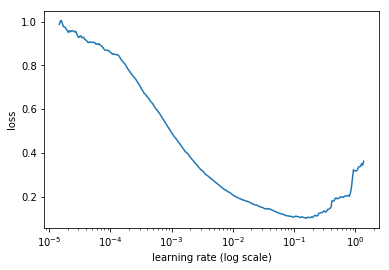
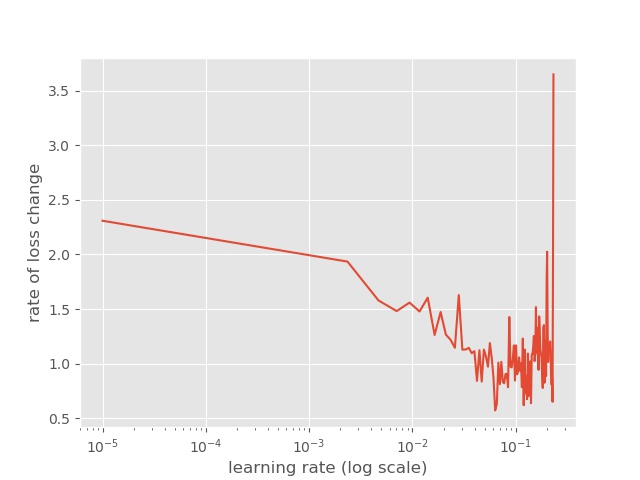
因此,对于训练深度学习模型,我们需要选择一个合理的学习率大小,既不能太大也不能太小。以往我们根据不同的学习率实验或者经验得到一个“认为”合理的学习率,但在在这篇文章 中提出了一种新方法: 在一个epoch中,首先,对优化器(比如SGD)设置一个非常低的学习率(如10-8),然后,在每次小batch数据训练中改变学习率(比如乘以某个因子),直到学习率达到一个非常高的值(如1或10)或者loss开始变大,停止训练,最后,我们将学习率和loss变化绘制在同张图中,如下图所示:
图2
仔细观察上图,会发现,一开始loss在减少,但是瞬间停止并且变大,这个主要是因为学习率非常低。但是,随着学习率的变大,loss在不断地降低,当学习率达到一个大(实际数值可能也很小)的值时,loss不降低反而开始增加。类似于前面提到的,高学习率可能会导致loss不断变大,因为loss可能不断在上下反弹,如图1所示。根据图2,我们能确定最佳的学习率大小吗? 是最小loss对应的学习率吗?
实际上,我们不应该选择最小loss对应的学习率,因为最小loss对应的学习率已经有点过高了,而且进一步训练可能也会出现loss增加的可能性。因此,我们一般选择最小loss对应的前一个学习率,这样我们可以快速地训练(主要是还有降低的空间)。例如,根据图2,我们应该选择1e-1学习率而不是1e-2。
备注 :任何SGD变体的优化器算法,我们都可以使用上述方法确定一个合理的学习率。我们只需训练一个epoch,将loss和学习率绘制到同张图上,根据上述分析就可以获得一个合理的学习率大小。
原理
如果你使用的是fastai模块,则非常容易实现该功能,即:
1 2 learner.lr_find() learner.sched.plot()
然后我们会得到类似图2的效果。使用fastai模块很容易实现,如果我们自己想实现呢,下面我将使用tensorflow eager模式实现该功能,在实现代码之前,我们先来理解下背后的计算逻辑,这样方便我们自己手动实现该方法。
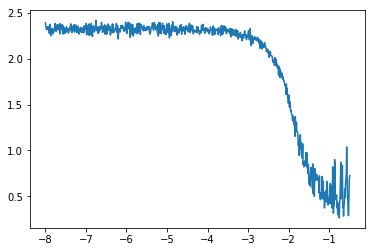
备注 :一般我们不会绘制每个小batch数据计算的损失,而是进行平滑之后,如果我们绘制原始的小batch数据损失变化,将得到一个如下图;
图3
虽然从该图中,我们仍然可以看到一个损失变化的趋势,但是并没有上一张图那么清晰。后面我们将使用scipy实现简单平滑操作。
首先,我们设置一个规则,当loss开始增加时,我们停止训练,在fastai模块中使用的标准是;
current loss > 4 × minimum loss \begin{equation*}
\hbox{current loss} > 4 \times \hbox{minimum loss}
\end{equation*}
current loss > 4 × minimum loss
前面我们提到,对于小batch数据训练过程中,我们对学习率进行更新,比如乘上一个因子,即:
lr i = lr 0 × q i \begin{equation*}
\hbox{lr}_{i} = \hbox{lr}_{0} \times q^{i}
\end{equation*}
lr i = lr 0 × q i
其中:
l r 0 lr_0 l r 0 q q q
下面,我们就是需要计算出这个更新因子的表达式,在训练之前,给定初始学习率和结束学习率即l r 0 lr_0 l r 0 l r n − 1 lr_{n-1} l r n − 1 q q q
lr N − 1 = lr 0 × q N − 1 ⟺ q N − 1 = lr N − 1 lr 0 ⟺ q = ( lr N − 1 lr 0 ) 1 N − 1 \begin{equation*}
\hbox{lr}_{N-1} = \hbox{lr}_{0} \times q^{N-1} \quad \Longleftrightarrow \quad q^{N-1} = \frac{\hbox{lr}_{N-1}}{\hbox{lr}_{0}} \quad \Longleftrightarrow \quad q = \left ( \frac{\hbox{lr}_{N-1}}{\hbox{lr}_{0}} \right )^{\frac{1}{N-1}}
\end{equation*}
lr N − 1 = lr 0 × q N − 1 ⟺ q N − 1 = lr 0 lr N − 1 ⟺ q = ( lr 0 lr N − 1 ) N − 1 1
进而,可以得到;
log ( lr i ) = log ( lr 0 ) + i log ( q ) = log ( lr 0 ) + i log ( lr N − 1 ) − log ( lr 0 ) N − 1 , \begin{equation*}
\log(\hbox{lr}_{i}) = \log(\hbox{lr}_{0}) + i \log(q) = \log(\hbox{lr}_{0}) + i\frac{\log(\hbox{lr}_{N-1}) - \log(\hbox{lr}_{0})}{N-1},
\end{equation*}
log ( lr i ) = log ( lr 0 ) + i log ( q ) = log ( lr 0 ) + i N − 1 log ( lr N − 1 ) − log ( lr 0 ) ,
为什么需要对l r 0 lr_0 l r 0 l r n − 1 lr_{n-1} l r n − 1 l r 0 lr_0 l r 0 l r n − 1 lr_{n-1} l r n − 1
lr i = lr 0 + i lr N − 1 − lr 0 N − 1 \begin{equation*}
\hbox{lr}_{i} = \hbox{lr}_{0} + i \frac{\hbox{lr}_{N-1} - \hbox{lr}_{0}}{N-1}
\end{equation*}
lr i = lr 0 + i N − 1 lr N − 1 − lr 0
但是,我们在初始化l r 0 lr_0 l r 0 l r n − 1 lr_{n-1} l r n − 1 l r 0 lr_0 l r 0 l r n − 1 lr_{n-1} l r n − 1 l r 0 lr_0 l r 0 l r n − 1 lr_{n-1} l r n − 1 l r n − 1 lr_{n-1} l r n − 1
代码实践
接下来,我们将基于Tensorflow eager模式来简单的实现lr_find功能。
首先,加载我们所需的模块:
1 2 3 4 5 6 7 import osimport tensorflow as tffrom matplotlib import pyplot as pltimport numpy as npfrom scipy.interpolate import splineplt.switch_backend('agg' )
其中,spline函数主要帮助我们实现简单的平滑化处理。
接下来,我们定义一个LrFinder类:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class LrFinder (): def __init__ (self, model,data_size,batch_szie,fig_path ): self .data_size = data_size self .batch_size = batch_szie self .loss_name = 'loss' self .eval_name = 'acc' self .width = 30 self .resiud = self .data_size % self .batch_size self .n_batch = self .data_size // self .batch_size self .model = model self .best_loss = 1e9 self .fig_path = fig_path self .losses = [] self .lrs = [] self .model_status = False self .learning_rate = tf.Variable(0.001 ,trainable=False )
其中:
model: 我们需要训练的模型
data_size: 数据集大小
batch_size: 批大小
fig_path: 保存图片的路径
另外,我们初始化了一个learning_rate变量,在Tensorflow中,我们将对learning_rate进行更新。
1 2 3 4 5 def on_batch_end (self, loss, ): self .lrs.append(self .learning_rate.numpy()) self .losses.append(loss.numpy())
上面,on_batch_end函数名表明了,我们应该在一个batch结束之后,运行该函数。首先,我们更新学习率和losses列表,我们将根据该列表进行绘制图标数据.
1 2 3 4 5 6 7 if loss.numpy() > self .best_loss * 4 : self .model_status = True if loss.numpy() < self .best_loss: self .best_loss = loss.numpy()
接着,我们对loss进行操作,若当前loss大于best_loss的四倍,则停止模型训练(该规则主要是从fastai模块中获取),其次对best_loss进行更新。
1 2 3 lr = self .lr_mult * self .learning_rate.numpy() self .learning_rate.assign(lr)
最后,我们对学习率进行更新,其中self.lr_mult是更新因子,在Tensorflow中对变量重新赋值主要是使用assign函数。
接下来,定义loss关于学习率变化绘制图表函数:
1 2 3 4 5 6 7 8 9 10 def plot_loss (self ): plt.style.use("ggplot" ) plt.figure() plt.ylabel("loss" ) plt.xlabel("learning rate" ) plt.plot(self .lrs, self .losses) plt.xscale('log' ) plt.savefig(os.path.join(self .fig_path,'loss.jpg' )) plt.close()
第一个函数plot_loss主要是对每个batch的loss进行绘制图表,类似图3。
1 2 3 4 5 6 7 8 9 10 11 def plot_loss_smooth (self ): xnew = np.linspace(min (self .lrs),max (self .lrs),100 ) smooth_loss = spline(self .lrs,self .losses,xnew) plt.ylabel("rate of loss change" ) plt.xlabel("learning rate (log scale)" ) plt.plot(xnew, smooth_loss) plt.xscale('log' ) plt.savefig(os.path.join(self .fig_path,'smooth_loss.jpg' )) plt.close()
第二个plot_loss_smooth函数,我们主要使用scipy模块中的spline函数简单实现一个平滑的效果。
最后,我们定义个拟合函数,对数据集进行训练并保存loss和lr变化。
1 2 3 4 5 6 7 8 9 10 11 def find (self, trainDatsset, start_lr, end_lr, optimizer,epochs=1 ,verbose = 1 ,save = True ): self .learning_rate.assign(start_lr) num_batches = epochs * self .data_size / self .batch_size self .lr_mult = (float (end_lr) / float (start_lr)) ** (float (1 ) / float (num_batches)) for i in range (epochs): for (batch_id, (X, y)) in enumerate (trainDatsset): y_pred,train_loss,grads = self .model.compute_grads(X, y) optimizer.apply_gradients(zip (grads, self .model.variables)) self .on_batch_end(loss=train_loss)
其中:
trainDataset:训练数据集,这里是Dataset格式
start_lr: 开始学习率,一般设置为0.000001
end_lr: 结束学习率,一般设置为10
optimizer: 优化器
epochs: 训练的epoch总数,在这里一般设置为1
verbose: 是否打印信息,默认为1
save: 是否保存图像
定义完lrFinder类后,我们只需类似模型训练过程一样构建即可,即:
1 2 3 4 5 6 7 from pytfeager.callbacks.lr_finder import LrFindermodel = CNN(num_classes = FLAGS.num_classes) lr_finder = LrFinder(model = model,data_size=buffer_size,batch_szie= FLAGS.batch_size,fig_path = fig_path) optimizer = tf.train.AdamOptimizer(learning_rate=lr_finder.learning_rate) lr_finder.find(trainDatsset=train_dataset,start_lr=0.00001 ,end_lr = 10 ,optimizer=optimizer,epochs=1 )
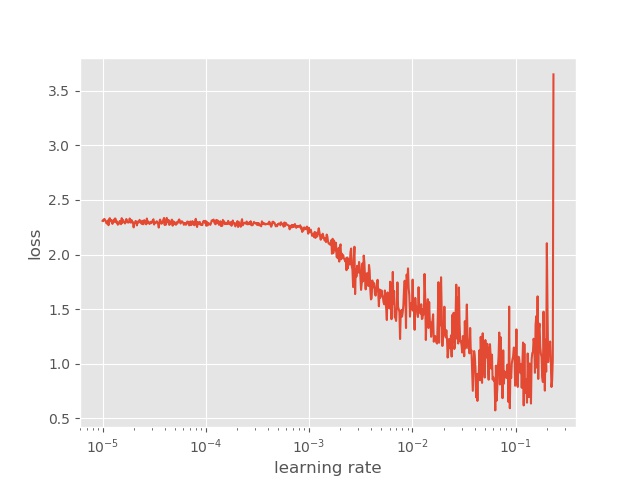
在mnist数据集上,我们可以得到以下结果:
平滑之后:
备注 :完整代码可在:github 上下载。