Transformer原理和实现

所谓 ”工预善其事，必先利其器“， BERT之所以取得这么惊才绝艳的效果，很大一部分原因源自于Transformer。为了后面更好、更快地理解BERT模型，这一节从Transformer的开山鼻祖说起，先来跟着”Attention is All You Need[1]“ 这篇文章，走近transformer的世界，在这里你再也看不到熟悉的CNN、RNN的影子，取而代之的是，你将看到Attention机制是如何被发挥的淋漓尽致、妙至毫颠，以及它何以从一个为CNN、RNN跑龙套的配角实现华丽逆袭。对于Bert来说，transformer真可谓天纵神兵，出匣自鸣！

看完本文，你大概能够：

• 掌握Encoder-Decoder框架
• 掌握残差网络
• 掌握BatchNormalization(批归一化)和LayerNormalization(层归一化)
• 掌握Position Embedding(位置编码)

当然，最重要的，你能了解Transformer的原理和代码实现。

Notes: 本文代码参考哈弗大学的The Annotated Transformer

Encoder-Decoder框架

Encoder-Decoder是为seq2seq（序列到序列）量身打造的一个深度学习框架，在机器翻译、机器问答等领域有着广泛的应用。这是一个抽象的框架，由两个组件：Encoder（编码器）和Decoder(解码器)组成。对于给定的输入source $(x_1, x_2, x_3, ...,x_n)$, 首先编码器将其编码成一个中间表示向量$z=(z_1, z_2, ..., z_n)$。接着，解码器根据z和解码器自身前面的输出，来生成下一个单词（如Figure 1所示）。

Figure 1

class EncoderDecoder(nn.Module):
    # A standard Encoder-Decoder architecture. Base for this and many other models.
    def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
        super(EncoderDecoder, self).__init__()
        self.encoder = encoder
        self.decoder = decoder
        self.src_embed = src_embed
        self.tgt_embed = tgt_embed
        self.generator = generator
    def forward(self, src, tgt, src_mask, tgt_mask):
        "Take in and process masked src and target sequences."
        return self.decode(self.encode(src, src_mask), src_mask,
                            tgt, tgt_mask)
    def encode(self, src, src_mask):
        return self.encoder(self.src_embed(src), src_mask)
    def decode(self, memory, src_mask, tgt, tgt_mask):
        return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)

上述代码呈现了一个标准的Encoder-Decoder框架。在实际应用中，编码器和解码器可以有多种组合，比如(RNN， RNN)、(CNN，RNN)等等，这就是传统的seq2seq框架。后来引入了attention机制，上述框架也被称为”分心模型“。为什么说他”分心“呢？因为对于解码器来说，他在生成每一个单词的时候，中间向量的每一个元素对当前生成词的贡献都是一样的。Attention的思想则是对于当前生成的单词，中间向量z的每个元素对其贡献的重要程度不同，跟其强相关的赋予更大的权重，无关的则给一个很小的权重。

举个例子: 假如我们要将 ”knowledge is power“ 翻译成中文，在翻译”knowledge“这个单词时， 显然”knowledge“这个单词对翻译出来的”知识“贡献最大，其他两个单词贡献就很小了。这实际上让模型有个区分度，不会被无关的东西干扰到，翻译出来的准确度当然也就更高了。在这里Attention其实还是一个小弟，主角仍然是RNN、CNN这些大佬.

我们不妨先顺着这个思路往下想，attention在这里充当了Encoder和Decoder的一个桥梁，事实证明有很好的效果。既然效果这么好，那在Encoder中是不是也可以用呢？文本自身对自身的编码进行有区分度的表示，事实上，这在以往的很多文本分类的工作中已被采用[2]。这看上去已经是个值得尝试的good idea了。继续开脑洞，Encoder都用了，Decoder能落后吗，好歹人家是一对CP，当然要妇唱夫随了。于是，Encoder和Decoder都用了自注意力（self-attention）。

回想一下，到这里我们已经在三个地方用到了注意力机制了。这时候RNN大佬不愿意了，原本我的名声地盘都被你们分走了，散伙！Attention反正是初生牛犊不怕虎，说好，分分账分道扬镳吧，反正你的序列计算并行不起来一直让人诟病，没你我可能更潇洒。于是两兄弟就分开了。相见时难别亦难，RNN老大哥深谋远虑，临走时不忘嘱咐一句”苟富贵，勿相忘！“。于是一个故事的结束就成了另一个故事的开始，注意力就此开启创业之路，寒来暑往，春去秋来，在黑暗中不断寻找光亮，学习PPT技巧，终于有一天，它的PPT做完了，找到了融资，破茧成蝶，横空出道，并给自己取了个亮闪闪的名字：Transformer， 自此，一个新的时代开始了。

整体架构

这部分我们来看看Transformer的架构。如Figure 2 所示， Transformer遵循了Encoder-Decoder的架构。在Encoder方面，6个编码器组件协同工作，组成一个大的编码器，解码器同样由6个解码器组件组成。我们先看Encoder。6个编码器组件依次排列，每个组件内部都是由一个多头attention加上一个前馈网络，attenion和前馈的输出都经过层归一化（LayerNormalization），并且都有各自的残差网络 。Decoder呢，组件的配置基本相同， 不同的是Decoder有两个多头attention机制，一个是其自身的mask自注意力机制，另一个则是从Encoder到Decoder的注意力机制，而且是Decoder内部先做一次attention后再接收Encoder的输出。

说完了Encoder和Decoder，再说说输入，模型的输入部分由词向量（embedding）经位置编码（positional Encoding）后输入到Encoder和Decoder。编码器的输出由一个线性层和softmax组成，将浮点数映射成具体的符号输出。

Figure 2 那么，下面我们将结合原理和代码来逐一了解这些部分。

Encoder

我们先来看下Encoder的实现。

class Encoder(nn.Module):
    "Core encoder is a stack of N layers"
    def __init__(self, layer, N):
        super(Encoder, self).__init__()
        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)
    def forward(self, x, mask):
        "Pass the input (and mask) through each layer in turn."
        for layer in self.layers:
            x = layer(x, mask)
        return self.norm(x)

以上便是Encoder的核心实现。它由N个encoderLayer组成。输入一次通过每个encoderLayer，然后经过一个归一化层。下面来看下encoderLayer和LayerNorm是什么样子。

EncoderLayer和残差网络

EncoderLayer如Figure 3所示。

Figure 3

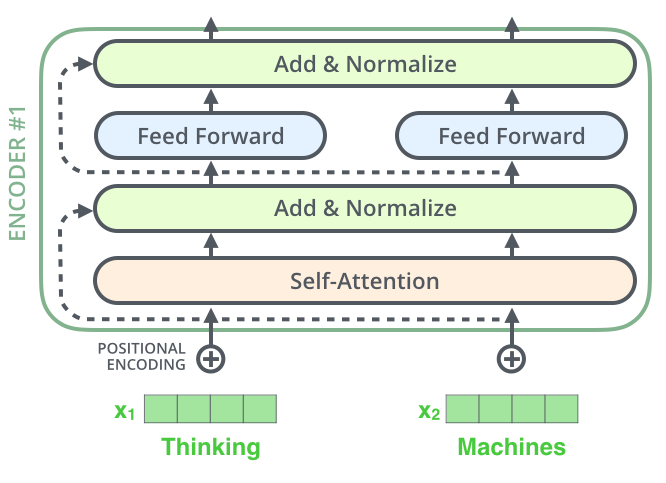
class EncoderLayer(nn.Module):
    "Encoder is made up of self-attn and feed forward (defined below)"
    def __init__(self, size, self_attn, feed_forward, dropout):
        super(EncoderLayer, self).__init__()
        self.self_attn = self_attn
        self.feed_forward = feed_forward
        self.sublayer = clones(SublayerConnection(size, dropout), 2)
        self.size = size

    def forward(self, x, mask):
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
        return self.sublayer[1](x, self.feed_forward)

class SublayerConnection(nn.Module):
    """
    A residual connection followed by a layer norm.
    Note for code simplicity the norm is first as opposed to last.
    """
    def __init__(self, size, dropout):
        super(SublayerConnection, self).__init__()
        self.norm = LayerNorm(size)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, sublayer):
        "Apply residual connection to any sublayer with the same size."
        return x + self.dropout(sublayer(self.norm(x)))

这里的代码初看上去有点绕，不过没关系，听我娓娓道来。我们先看什么是残差网络（即代码中的SublayerConnection），见Figure 4 。其实非常简单，就是在正常的前向传播基础上开一个绿色通道，这个通道里x可以无损通过。这样做的好处不言而喻，避免了梯度消失（求导时多了一个常数项）。最终的输出结果就等于绿色通道里的x加上sublayer层的前向传播结果。注意，这里输入进来的时候做了个norm归一化，关于norm我们后面再说。

Figure 4 理解了残差网络，EncoderLayer的代码就很好看懂了。sublayer有两个，一个是多头self-attention层，另一个是前馈网络（feed_forward）。输入x先进入多头self-attention，用一个残差网络加成，接着通过前馈网络， 再用一个残差网络加成。

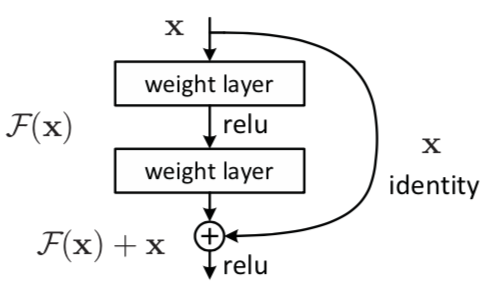
让我们从输入x开始，再从头理一遍这个过程:

• 输入x
• x做一个层归一化： x1 = norm(x)
• 进入多头self-attention: x2 = self_attn(x1)
• 残差加成：x3 = x + x2
• 再做个层归一化：x4 = norm(x3)
• 经过前馈网络: x5 = feed_forward(x4)
• 残差加成: x6 = x3 + x5
• 输出x6

以上就是一个Encoder组件所做的全部工作了。里面有两点暂未说明，一个是多头attention， 另一个是层归一化。喝杯茶之后精彩继续。

多头注意力机制

多头注意力机制在敝人之前的博客已经做了详尽的原理和代码解析(请戳)，这里不再赘述，仅贴一下代码和注释，这里使用的是点乘attention，而不是加性（additive）attention。但是再提一点，在encoder和decoder的自注意力中，attention层的输入分为self_attn(x, x, x, mask)和self_attn(t, t, t, mask)， 这里的x和t分别为source和target输入。后面会看到，从encoder到decoder层的注意力输入时attn(t, m, m), 这里的m是Encoder的输出。

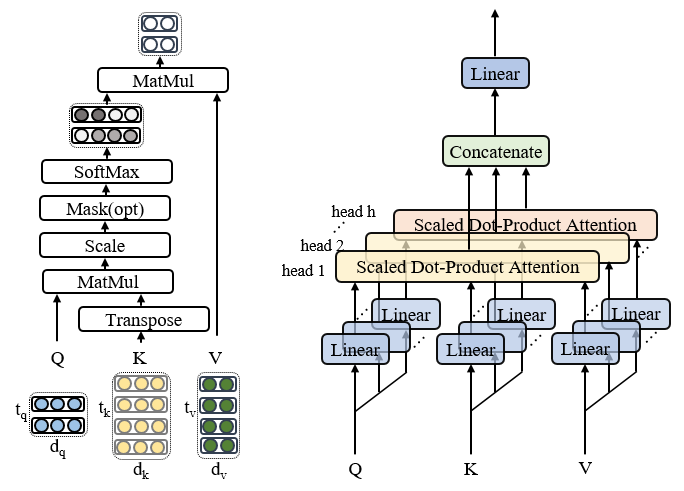
def attention(query, key, value, mask=None, dropout=None):
    #因子化的点乘Attention-矩阵形式
    #Query： 查询 （batch_size, heads, max_seq_len, d_k）
    #Key: 键 (batch_size, heads, max_seq_len_d_k)
    #Value: 值 （batch_size, heads, max_seq_len, d_v）
    #d_v = d_k
    #Q=K=V
    d_k = query.size(-1)
    # (batch_size, heads, max_seq_len, d_k) * (batch_size, heads, d_k, max_seq_len)
    #  = (batch_size, heads, max_seq_len, max_seq_len)
    # 为了方便说明，只看矩阵的后两维 (max_seq_len, max_seq_len), 即
    #       How  are  you
    # How [[0.8, 0.2, 0.3]
    # are  [0.2, 0.9, 0.6]
    # you  [0.3, 0.6, 0.8]]
    # 矩阵中每个元素的含义是，他对其他单词的贡献（分数）
    # 例如，如果我们想得到所有单词对单词“How”的打分，取矩阵第一列[0.8, 0.2, 0.3], 然后做softmax
    scores = torch.matmul(query, key.transpose(-2, -1)) \
             / math.sqrt(d_k)
    # 对于padding部分，赋予一个极大的负数，softmax后该项的分数就接近0了，表示贡献很小
    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e9)
    p_attn = F.softmax(scores, dim = -1)
    if dropout is not None:
        p_attn = dropout(p_attn)
    # 接着与Value做矩阵乘法:
    # (batch_size, heads, max_seq_len, max_seq_len) * (batch_size, heads, max_seq_len, d_k)
    # = (batch_size, heads, max_seq_len, d_k)
    return torch.matmul(p_attn, value), p_attn

class MultiHeadedAttention(nn.Module):
    def __init__(self, h, d_model, dropout=0.1):
        "Take in model size and number of heads."
        super(MultiHeadedAttention, self).__init__()
        assert d_model % h == 0, "heads is not a multiple of the number of the in_features"
        # We assume d_v always equals d_k
        self.d_k = d_model // h
        self.h = h
        self.linears = clones(nn.Linear(d_model, d_model), 4)
        self.attn = None
        self.dropout = nn.Dropout(p=dropout)

    def forward(self, query, key, value, mask=None):
        #这里的query, key, value与attention函数中的含义有所不同，这里指的是原始的输入.
        #对于Encoder的自注意力来说，输入query=key=value=x
        #对于Decoder的自注意力来说，输入query=key=value=t
        #对于Encoder和Decoder之间的注意力来说， 输入query=t， key=value=m
        #其中m为Encoder的输出，即给定target，通过key计算出m中每个输出对当前target的分数，在乘上m
        if mask is not None:
            # Same mask applied to all h heads.
            mask = mask.unsqueeze(1)
        nbatches = query.size(0)
        # 1) Do all the linear projections in batch from d_model => h x d_k
        query, key, value = \
            [l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
             for l, x in zip(self.linears, (query, key, value))]
        # 2) Apply attention on all the projected vectors in batch.
        ##   x: (batch_size, heads, max_seq_len, d_k)
        x, self.attn = attention(query, key, value, mask=mask,
                                 dropout=self.dropout)
        # 3) "Concat" using a view and apply a final linear.
        ##   x: (batch_size, max_seq_len, d_k*h)
        x = x.transpose(1, 2).contiguous() \
            .view(nbatches, -1, self.h * self.d_k)
        ## output: (batch_size, max_seq_len, d_model)
        return self.linears[-1](x)

def clones(module, N):
    "Produce N identical layers."
    return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])

注意下attention当中的mask。我们之前提到，在三个地方用到了attention。在Encoder的自注意力机制中，mask是用来过滤padding部分的作用，对于source中的每一个词来讲，其他的词对他都是可见的，都可以做出贡献的。但是在Decoder中，mask的作用就有所不同了。这可能又要从Encoder-Decoder框架说起。在这个框架下，解码器实际上可看成一个神经网络语言模型，预测的时候，target中的每一个单词是逐个生成的，当前词的生成依赖两方面：

• 一是Encoder的输出.
• 二是target的前面的单词.

例如，在生成第一个单词是，不仅依赖于Encoder的输出，还依赖于起始标志[CLS]；生成第二个单词是，不仅依赖Encoder的输出，还依赖起始标志和第一个单词$\dots$依此类推。这其实是说，在翻译当前词的时候，是看不到后面的要翻译的词。由上可以看出，这里的mask是动态的。

def subsequent_mask(size):
    "Mask out subsequent positions."
    # size: 序列长度
    attn_shape = (1, size, size)
    # 生成一个上三角矩阵
    subsequent_mask = np.triu(np.ones(attn_shape), k=1).astype('uint8')
    return torch.from_numpy(subsequent_mask) == 0

下面详细介绍下subsequent_mask是如何起作用的。函数的参数size指的是target句子的长度。以”[CLS] That is it“这个长度为4的target输入为例，这个函数的输出是什么呢？

print(subsequent_mask(size=4))

tensor([[[1, 0, 0, 0],
         [1, 1, 0, 0],
         [1, 1, 1, 0],
         [1, 1, 1, 1]]], dtype=torch.uint8)

可以看到，输出为一个下三角矩阵，维度为（1,4,4）。现在我们再来看下attention函数，mask起作用的地方是在Query和Key点乘后，结果矩阵的维度为（batch_size, heads, max_seq_len, max_seq_len）。为方便起见，我们只看一条数据，即batch_size=1。进入多头attention时，注意到对mask做了一步操作：

mask = mask.unsqueeze(1)
mask：
tensor([[[[1, 0, 0, 0],
          [1, 1, 0, 0],
          [1, 1, 1, 0],
          [1, 1, 1, 1]]]], dtype=torch.uint8)

这时mask的维度变成了（1,1,4,4）.

target:
         CLS  That is   it
 CLS [[[[0.8, 0.2, 0.3, 0.9]
 That   [0.2, 0.9, 0.6, 0.4]
 is     [0.3, 0.6, 0.8, 0.7]
 it     [1.2, 0.6, 2.1, 3.2]]]]

mask：
       [[[[1,  0,   0,  0],
          [1,  1,   0,  0],
          [1,  1,   1,  0],
          [1,  1,   1,  1]]]]

写成了上面的样子，mask的作用就很显然了。例如，对于”CLS“来说，预测它下一个词时，只有”CLS“参与了attention，其他的词（相对于CLS为未来的词）都被mask_fill掉了，不起作用。后面的情况依此类推。

细心的小伙伴可能发现了，这里的解释并没有考虑padding部分。事实上，就算加了padding部分（为0），也不影响上述过程，有兴趣的话可以在上面it后面加上个0，下面的矩阵加一列[0 0 0 0 ]， 就可以一目了然。

层归一化

class LayerNorm(nn.Module):
    "Construct a layernorm module (See citation for details)."
    def __init__(self, features, eps=1e-6):
        super(LayerNorm, self).__init__()
        self.a_2 = nn.Parameter(torch.ones(features))
        self.b_2 = nn.Parameter(torch.zeros(features))
        self.eps = eps

    def forward(self, x):
        mean = x.mean(-1, keepdim=True)
        std = x.std(-1, keepdim=True)
        return self.a_2 * (x - mean) / (std + self.eps) + self.b_2

在前面多次用到了层归一化（LayerNormalization），那么它是何方神圣呢？或许你对BatchNormalization比较熟悉，但千万不要在这里错以为是它。可以说层归一化是BatchNormalization的2.0版本，它是由Hinton神和他的学生提出的[3]。

BatchNormalization

BatchNormalization的出现无疑是广大AI调参侠的福音，将大家从繁琐的权重初始化、学习率调节中释放出来。它不仅能够大大加快收敛速度，还自带正则化功能，是Google 2015年提出的[4]。

机器学习的一个重要的假设是：数据是独立同分布的。训练集合测试集的数据是同分布的，这样模型才有好的泛化效果。神经网络其实也是在学习这个分布。在这个假设前提下，一旦我们知道了（x，y）的联合分布，很多问题就能通过条件概率$P(x|y)$计算出来了。但是在实际训练过程中，数据经过前一个隐藏层向后一个隐藏层传播（线性+非线性运算），分布通常会发生变化（作者称之为Internal Covariate Shift），这会导致网络学习变慢。我们从两个方面来稍微理解一下这个问题。

一方面：我们现在只看两个隐藏层（隐藏层A和隐藏层B）之间的传播。第一轮，来自A的数据经过线性操作和激活函数后到达B，反向传播时，B层为了学习到这个分布（满足A的需求），调整了权重W1。接着又进行第二轮传播了，A数据一到B，A说，现在需求变了，要这样这样。B一脸懵，盘算了一下，发现前面的白学了，没办法，换个方向重来，就这样，A一直在变，B就得跟着变，来来回回磨合，这听起来就是个非常耗时的工作。就好比A说今天要吃汤圆，B和好了面粉，准备了调料，A又说我要吃饭，虽然在B的不懈努力下A最后能吃上饭，但如果一开始A就告诉B我要吃饭不是更快一点？，网络越深，这个问题就越严重。

另一方面则是与激活函数有关，我们用sigmoid为例来说明一下。假设两层传播之间可表示为

$$z = g(Wu+b)$$

其中g是sigmoid函数，我们令

$$x=Wu+b$$

那么:

$$z = sigmoid(x) = g(x) = \frac{1}{1+exp(-x)}$$

计算下梯度：

$$\frac{\partial z}{\partial W} = \frac{\partial z}{\partial g}\cdot\frac{\partial g}{\partial x}\cdot\frac{\partial x}{\partial u}$$

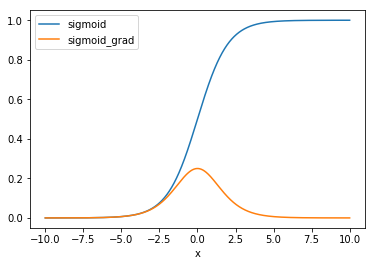
我们关注一下中间那一项，是sigmoid函数的导数，它的分布如Figure 5 所示，可见随着x不断增大，该项趋近于0，这也就意味着整个梯度趋近于0，进入饱和区了，导致的结果就是收敛变慢！要想加快收敛怎么办，把x拉到靠近0的位置就行了，这里导数值最大。

Figure 5 BatchNormalization就是解决这两个问题的。首先，它将隐藏层的输入强行变换为同一分布（解决了第一个问题），这个分布就是正态分布（解决了第二个问题）。

它的具体做法如Figure 6所示。对每一个Mini-Batch的所有样本的每一维特征，计算两个统计量：均值和方差，然后做一个归一化操作，这样就变成了正态分布了。但是只这样做也有问题，首先，谁说数据一定是正态分布的，偏正态不行吗？第二，把数据全部拉到接近0的位置，sigmoid不就接近于一个线性函数了吗，没有起到激活的作用啊（线性激活函数+线性操作等价于一层线性操作）。

Figure 6 为了解决这两个问题，作者又做了一步操作，引入了两个参数gamma和beta（图中的最后一步）, 这两个参数是在训练过程中学习的！相当于将这个正态分布左右挪了挪，变胖或者变瘦，在加快收敛速度和保持非线性的之间找到一个平衡。当然这是臆测的，作者并没有明确这么说。如果你非要问为什么，那我只能告诉你深度学习是个实验领先于理论的学科。

上面说了一下训练过程。那么预测的时候呢？假如只预测一个样本，一个样本的均值…方差…怎么算?没意义是吧。事实上，预测的时候用的是全局的均值和方差，这个全局的均值和方差是怎么得到的呢？很简单，训练过程中记录下每个Mini-Batch的均值和方差，求个期望就是全局的均值和方差了。

LayerNormalization

BatchNormalization简直是个救世主啊，它令调参工作变得从未如此容易，让调参侠们不费吹灰之力，谈笑间到达收敛的彼岸。但毛主席曾经说过，万物都是辩证的，它同样存在两个问题：

• 对batch_size非常敏感。BatchNormalization的一个重要出发点是保持每层输入的数据同分布。回想下开始那个独立同分布的假设。假如取的batch_size很小，那显然有些Mini-Batch的数据分布就很可能与整个数据集的分布不一致了，又出现了那个问题，数据分布不一致，这就等于说没起到同分布的作用了，或者说同分布得不充分。实验也证明，batch_size取得大一点， 数据shuffle的好一点，BatchNormalization的效果就越好。

• 不能很方便地用于RNN。这其实是第一个问题的引申。我们再来看一下Figure 6中的均值和方差的计算公式。对所有样本求均值。对于图片这类等长的输入来说，这很容易操作，在每个维度加加除除就可以了，因为维度总是一致的。而对于不等长的文本来说，RNN中的每个time step共享了同一组权重。在应用BatchNormalization时，这就要求对每个time step的batch_size个输入计算一个均值和方差。那么问题就来了，假如有一个句子S非常长，那就意味着对S而言，总会有个time_step的batch_size为1，均值方差没意义，这就导致了BatchNormalization在RNN上无用武之地了。

为了避免这两个问题，LayerNormalization就应运而生了。

LayerNormalization的主要变化在于：

• 不再对Mini-Batch中的N的样本在各个维度做归一化，而是针对同一层的所有神经元做归一化。归一化公式为：

  $$\mu^l = \frac{1}{H}\Sigma_1^Ha_i^l$$

  $$\sigma^l = \sqrt{\frac{1}{H}\Sigma_1^H(a_i^l-\mu^l)}$$

  其中，H指的是一层神经网络的神经元个数。我们再回想下BatchNormalization，其实它是在每个神经元上对batch_size个数据做归一化，每个神经元的均值和方差均不相同。而LayerNormalization则是对所有神经元做一个归一化，这就跟batch_size无关了。哪怕batch_size为1，这里的均值和方差只和神经元的个数有关系（如果读到这里仍然感到不是特别清楚，再读两遍，还困惑也没关系，待会看Figure 7）。

• 测试的时候可以直接利用LN，所以训练时不用保存均值和方差，这节省了内存空间。

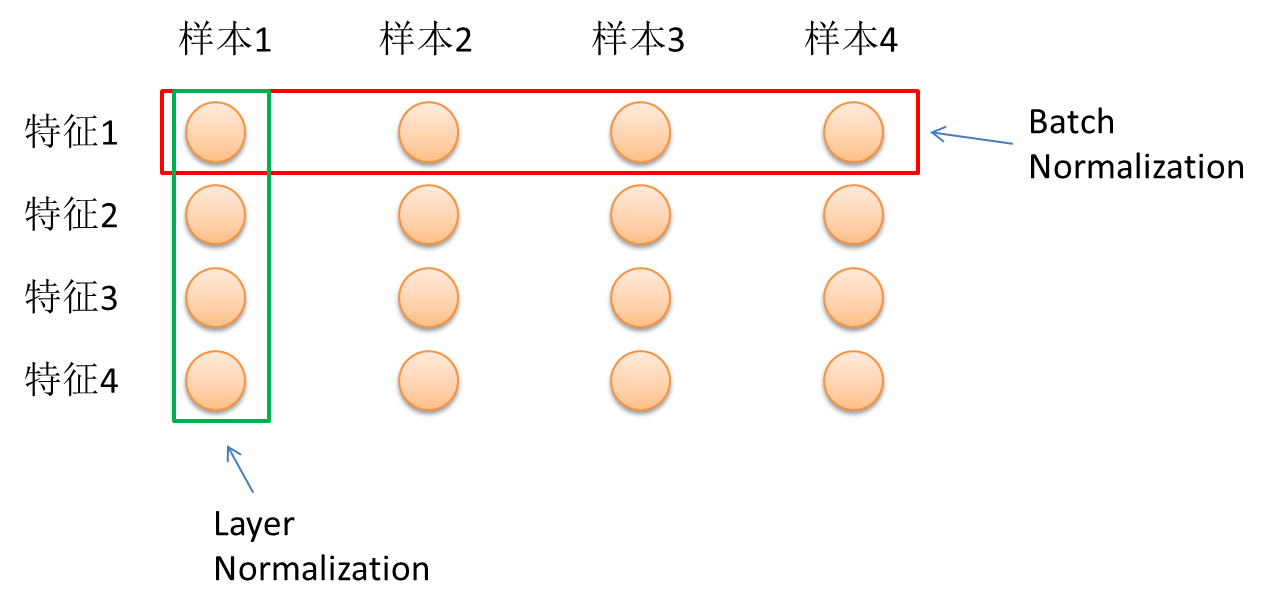
Figure 7示意了两种方式的区别。假设有N个样本，每个样本的特征维度为4，图中每个小圆代表一个特征，特征1，特征2等等，特征4。BatchNormalization是在N个同一特征（如特征1）上求均值和方差，这里要对每个特征求1次，共4次。对照一下上面说的，万一有个样本有5个特征，是不是就没法玩了。LayerNormalization呢，别的样本都和我没啥关系，有多少个特征我把这些特征求个均值方差就好了。这也就是为什么一个叫”批归一化“，另一个叫”层归一化“了。理解了这一点，也就理解了为什么Transformer中使用LN而不是BN。

Figure 7 当然BatchNormalization也不是吃素的，虽然它在处理不等长序列上存在天生的缺陷，但是除此之外，它的效果都要好于其他Normalization方式（比如LN，WN，IN）。直觉上，BN貌似更好理解一点，LN似乎有种胡子眉毛一把抓的感觉。

回到层归一化的代码中，注意到这里的求均值和方差均是应用在x的最后一维上。这一维其实就是in_features，即神经元个数，同BN一样，这里也引入两个参数，参与训练。如果你想问这样做为什么也会有效，我愿意再次告诉你深度学习是个实验领先于理论的学科，当然，不排除某位数学大神能够看出两者之间存在某种等价性。

前馈网络

每个encoderLayer中，多头attention后会接一个前馈网络。这个前馈网络其实是两个全连接层，进行了如下操作：

$$\mathrm{FFN}(x)=\max(0, xW_1 + b_1) W_2 + b_2$$

class PositionwiseFeedForward(nn.Module):
    '''Implements FFN equation.
    d_model=512
    d_ff=2048
    '''
    def __init__(self, d_model, d_ff, dropout=0.1):
        super(PositionwiseFeedForward, self).__init__()
        self.w_1 = nn.Linear(d_model, d_ff)
        # self.w_1 = nn.Conv1d(in_features=d_model, out_features=d_ff, kenerl_size=1)
        self.w_2 = nn.Linear(d_ff, d_model)
        # self.w_2 = nn.Conv1d(in_features=d_ff, out_features=d_model, kenerl_size=1)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        return self.w_2(self.dropout(F.relu(self.w_1(x))))

这两层的作用等价于两个 kenerl_size=1的一维卷积操作。

词向量

这里就是普通的不能再普通的词向量，将词语变成d_model维的向量。

class Embeddings(nn.Module):
    def __init__(self, d_model, vocab):
        super(Embeddings, self).__init__()
        self.lut = nn.Embedding(vocab, d_model)
        self.d_model = d_model

    def forward(self, x):
        return self.lut(x) * math.sqrt(self.d_model)

位置编码

由于Transformer没有用到CNN和RNN，因此，句子单词之间的位置信息就没有利用到。显然，这些信息对于翻译来说是非常有用的，同样一句话，每个单词的意思能够准确的翻译出来，但如果顺序不对，表达出来的意思就截然不同了。举个栗子感受一下，原句：”A man went through the Big Buddhist Temple“, 翻译成：”人过大佛寺“和”寺佛大过人“，意思就完全不同了。

那么如何表达一个序列的位置信息呢？对于某一个单词来说，他的位置信息主要有两个方面：一是绝对位置，二是相对位置。绝对位置决定了单词在一个序列中的第几个位置，相对位置决定了序列的流向。作者利用了正弦函数和余弦函数来进行位置编码：

$$PE_{(pos,2i)} = sin(pos / 10000^{2i/d_{\text{model}}})$$

$$PE_{(pos,2i+1)} = cos(pos / 10000^{2i/d_{\text{model}}})$$

其中pos是单词处于句子的第几个位置。我们来考察一下第一个公式，看是否每个位置都能得到一个唯一的值作为编码。为简单起见，不妨令i=0，那么：

$$PE_{(pos,0)} = sin(pos)$$

我们反过来想，假如存在位置j和k的编码值相同，那么就有：

$$sin(i)=sin(j)$$

$i, j $为非负整数且$i$不等于$j$

以上两式需要同时满足，可等价为：

$$i=(-1)^k\cdot j+k\cdot{\pi}$$

$i, j $为非负整数且$i$不等于$j$且$k$为整数

同时成立，这就意味着：

$$\pi=\frac{[i-(-1)^k\cdot j]}{k}$$

这显然是不可能的，因为左边是个无理数（无限不循环小数），而右边是个有理数。通过反证法就证明了在这种表示下，每个位置确实有唯一的编码。

上面的讨论并未考虑i的作用。i决定了频率的大小，不同的i可以看成是不同的频率空间中的编码，是相互正交的，通过改变i的值，就能得到多维度的编码，类似于词向量的维度。这里$2i<=512$（d_model）, 一共512维。想象一下，当2i大于d_model时会出现什么情况，这时sin函数的周期会变得非常大，函数值会非常接近于0，这显然不是我们希望看到的，因为这样和词向量就不在一个量级了，位置编码的作用被削弱了。另外，值得注意的是，位置编码是不参与训练的，而词向量是参与训练的。作者通过实验发现，位置编码参与训练与否对最终的结果并无影响。

class PositionalEncoding(nn.Module):
    "Implement the PE function."
    def __init__(self, d_model, dropout, max_len=5000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)

        # Compute the positional encodings once in log space.
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2) *
                             -(math.log(10000.0) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)
        self.register_buffer('pe', pe)

    def forward(self, x):
        x = x + Variable(self.pe[:, :x.size(1)],
                         requires_grad=False)
        return self.dropout(x)

之所以对奇偶位置分别编码，是因为编码前一个位置是可以由另一个位置线性表示的（公差为1的等差数列），在编码之后也希望能保留这种线性。我们以第1个位置和第k+1个位置为例，还是令i=0：

$$PE(1, 0)=cos(1)$$

$$PE(k,0) = sin(1+k) = sin(1)cos(k)+cos(1)sin(k) = A+B\cdot PE(1,0)$$

---

至此，我们就把Encoder部分的细节介绍完了，下面来看下Decoder部分

---

Deocder

我们先在看一眼刚开始的那张框架图。左半部分是Encoder，右半部分是Decoder。不难看出，Decoder和Encoder极其相似。

首先，Decoder也是由6个相同的decoder组件构成。

class Decoder(nn.Module):
    "Generic N layer decoder with masking."
    def __init__(self, layer, N):
        super(Decoder, self).__init__()
        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)
    def forward(self, x, memory, src_mask, tgt_mask):
        for layer in self.layers:
            x = layer(x, memory, src_mask, tgt_mask)
        return self.norm(x)

每个组件长什么样子呢？首先输入经过词向量和位置编码，进入target的自注意力层，这里和Encoder一样，也是用了残差和层归一化。然后呢，这个输出再和Encoder的输出做一次context attention，相当于把上面的那层重复了一次，唯一不同的是，这次的attention有点不一样的，不再是自注意力，所有的技术细节都可以参照Encoder部分，这里不再复述。

class DecoderLayer(nn.Module):
    "Decoder is made of self-attn, src-attn, and feed forward (defined below)"
    def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
        super(DecoderLayer, self).__init__()
        self.size = size
        self.self_attn = self_attn
        self.src_attn = src_attn
        self.feed_forward = feed_forward
        self.sublayer = clones(SublayerConnection(size, dropout), 3)

    def forward(self, x, memory, src_mask, tgt_mask):
        m = memory
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
        x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
        return self.sublayer[2](x, self.feed_forward)

线性层和softmax

这是整个模型的最后一步了。从Decoder拿到的输出是维度为（batch_size, max_seq_len, d_model）的浮点型张量，我们希望得到最终每个单词预测的结果，首先用一个线性层将d_model映射到vocab的维度，得到每个单词的可能性，然后送入softmax，找到最可能的单词。

线性层的参数个数为d_mode $\star$ vocab_size， 一般来说，vocab_size会比较大，拿20000为例，那么只这层的参数就有$512 \star 20000$个，约为10的8次方，非常惊人。而在词向量那一层，同样也是这个数值，所以，一种比较好的做法是将这两个全连接层的参数共享，会节省不少内存，而且效果也不会差。

class Generator(nn.Module):
    "Define standard linear + softmax generation step."
    def __init__(self, d_model, vocab):
        super(Generator, self).__init__()
        self.proj = nn.Linear(d_model, vocab)
    def forward(self, x):
        return F.log_softmax(self.proj(x), dim=-1)

结语

至此，整个Transformer模型的介绍就告一段落了，希望读者能够有所收获。以上恭疏短引，已竭鄙怀。请洒潘江，各倾陆海云尔！

参考文献

• Attention is all your need
• Multilingual Hierarchical Attention Networks for Document Classification
• Layer Normalization
• Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift