常用的机器学习算法衡量指标

你可能在你的机器学习研究或项目中使用分类精度、均方误差这些方法衡量模型的性能。当然，在进行实验的时候，一种或两种衡量指标并不能说明一个模型的好坏，因此我们需要了解常用的几种机器学习算法衡量指标。本文整理介绍了最常用的机器学习算法衡量指标：分类精度、对数损失、混淆矩阵、曲线下面积、F1分数、平均绝对误差、均方误差…。相信阅读之后你能对这些指标有系统的理解。(后续会不断的增加)

评估机器学习算法是项目的一个重要部分。你的模型可能在用一个指标来评论时能得到令人满意的结果，但用其他指标(如对数损失或其他指标)进行评估时，可能会给出较差的结果。大多数时候，我们使用分类的准确性来衡量我们的模型的性能，然而这还不足真正判断我们的模型。在这篇文章中，我们将介绍可用的不同类型的评估指标。

1. 常见的衡量指标
1.1 分类精度
1.2 对数损失
1.3 混淆矩阵
1.4 曲线下面积(AUC))
1.5 F1分数
1.6 平均绝对误差
1.7 均方误差
1.8 均方根误差
1.9 Gini系数
1.10 KS指标

1.1分类精度

当我们使用`准确性`这个术语时，指的就是分类精度。它是正确预测数与样本总数的比值.

$Accuracy = \frac{Number \quad of \quad Correct \quad predictions}{Total \quad number \quad of \quad predictions \quad made}$

只有当属于每个类的样本数量相等时，它才有效。

例如，假设在我们的训练集中有98％的A类样本和2％的B类样本。然后，我们的模型可以通过简单预测每个训练样本都属于A类而轻松获得98％的训练准确性。

当在60％A级样品和40％B级样品的测试集上采用相同的模型时，测试精度将下降到60％。分类准确度很重要，但是它有时会带给我们一种错觉，使我们认为模型已经很好。

真正的问题出现在，当少量样本类被误分类造成很大的损失的情况下。如果我们处理一种罕见但致命的疾病，那么真正的患者未被诊断出疾病的造成的损失远高于健康人未被诊断出疾病。

1.2对数损失-Logarithmic Loss

对数损失(logloss)，通过惩罚错误的分类来来量化分类器的准确度,最小化对数损失等同于最大化分类精度.它适用于多类分类。在处理对数损失时，分类器必须为所有样本分配属于每个类的概率。假设，有N个样本属于M类，那么对数损失的计算如下:

$LogarithmicLoss = \frac{-1}{N}\sum_{i = 1}^{N}\sum_{j = 1}^{M} y_{ij} * \log (p_{ij})$

这里;

$y_{ij}$ 表示样本i是否属于类别j
$p_{Ij}$ 表示样本i属于类j的概率

对数损失的值没有上限，它取值于[0，∞）范围内。对数损失接近0表示其有高的准确性，而如果对数损失远离0则表明准确度较低。

一般来说，最大限度地减少对数损失可以提高分类精度。

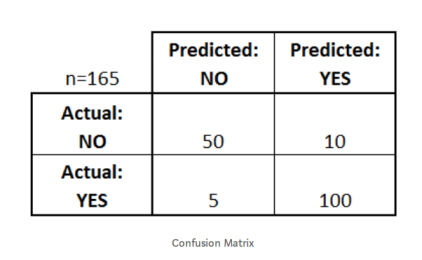
1.3 混淆矩阵-Confusion Matrix

混淆矩阵顾名思义，通过一个矩阵描述了模型的完整性能。

假设我们有一个二元分类问题。我们有一些样本，它们只属于两个类别:是或否。另外，我们有自己的分类器，它用来预测给定输入样本的类。我们在165个样品上测试了我们的模型，得到了如下结果:

有四个重要的术语:

True Positives：我们预测“是”并且实际产出也是“是”的情况,对应上图中的100

True Negatives：我们预测“否”和实际产出也是“是”的情况对应上图中的5

False Positives：我们预测“是”并且实际产出也是“否”的情况,对应上图中的10

False Negatives：我们预测“否”并且实际产出也是“否”的情况,对应上图中的50

矩阵的精度可以通过取过主对角线的平均值来计算。即，

$Accuracy = \frac{TruePositives + FalseNegatives}{TotalNumberofSamples}$

比如上面的例子:

$Accuracy = \frac{100 + 50}{165} = 0.91$

混淆矩阵是其他度量类型的基础。

1.4 曲线下面积（Area Under Curve, AUC）

`曲线下面积(AUC)`是评估中使用最广泛的指标之一。它用于二分类问题。分类器的`AUC`等价于分类器随机选择正样本高于随机选择负样本的概率。在定义`AUC`之前，让我们理解两个基本术语：

True Positive Rate (真阳性率)：它被定义为TP /（FN + TP）。对于所有正数据点，它对应于正数据点被正确认为是正的比例。

$TruePositiveRate = \frac{TruePositive}{FalseNegative + TruePositive}$

False Positive Rate(假阳性率) :它被定为FP /（FP + TN）。即对应于所有负数据点，负数据点被错误地认为是正的比例。

$FalsePositiveRate = \frac{FalsePositive}{FalsePositive + TrueNegative}$

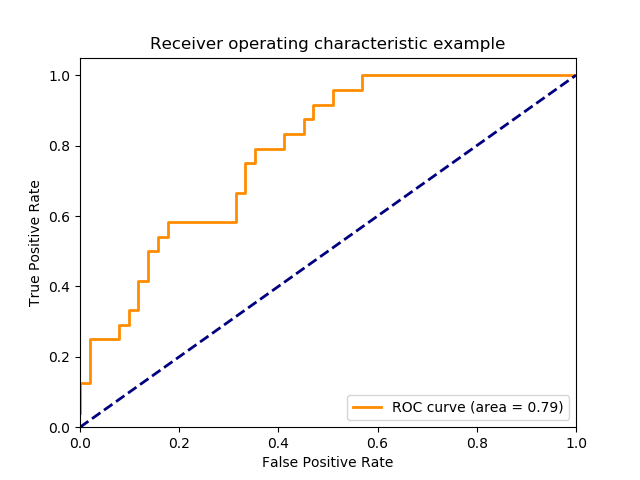
False Positive Rate 和 True Positive Rate的值均在[0，1]范围内。FPR和TPR机器人在阈值如（0.00，0.02，0.04，…，1.00）下计算并绘制对应图形。AUC是[0,1]中不同点的False Positive Rate对True Positive Rate曲线下的面积。

很明显，AUC的范围是[0,1]。值越大，我们模型的性能越好.

1.5 F1 分数-F1 Score

F1分数用于衡量测试的准确性

F1分数是精确度和召回率之间的调和平均值（Harmonic Mean）。 F1分数的范围是[0，1]。它会告诉您分类器的精确程度（正确分类的实例数），以及它的稳健程度（它不会错过大量实例）。

高精度和低召回率，会带来高的精度，但也会错过了很多很难分类的实例。 F1得分越高，我们模型的表现越好。在数学上，它可以表示为：

$F1 = 2* \frac{1} {\frac{1}{precision}+\frac{1}{recall}}$

F1分数试图找到精确度和召回率之间的平衡。

Precision :它是正确的正结果的数目除以分类器所预测的正结果的数目。

$precision = \frac{TruePositives}{TruePositives + FalsePositives}$

Recall：它是正确的正结果的数量除以所有相关样本(即所有应该被识别为正结果的样本)的数量。

$recall = \frac{TruePositives}{TruePositives + FalseNegatives}$

1.6 平均绝对误差-Mean Absolute Error

平均绝对误差是原始值与预测值之差的平均值。它衡量预测与实际输出还差多远。但是，它们并没有给我们提供任何关于错误方向的信息，即不能给出我们的模型到底是低于预测数据还是高于预测数据。在数学上，它表示为：

$MeanAbsoluteError = \frac{1}{N}\sum_{j = 1}^{N} | y_j - \hat{y}_{j}|$

1.7 均方误差Mean Squared Error

均方误差（MSE）与平均绝对误差非常相似，唯一的区别是MSE取原始值与预测值之差的平方的平均值。 MSE的优点是计算梯度更容易，而平均绝对误差需要复杂的线性编程工具来计算梯度。由于我们采用误差的平方，更大的误差的影响变得更明显，因此模型现在可以更多地关注更大的误差。

$MeanSquaredError = \frac{1}{N}\sum_{j = 1} ^{N} (y_j - \hat{y}_j)^2$

1.8 均方根误差-RMSE

它是观测值与真值偏差的平方和观测次数n比值的平方根，在实际测量中，观测次数n总是有限的，真值只能用最可信赖（最佳）值来代替.方根误差对一组测量中的特大或特小误差反映非常敏感，所以，均方根误差能够很好地反映出测量的精密度。均方根误差，当对某一量进行甚多次的测量时，取这一测量列真误差的均方根差(真误差平方的算术平均值再开方)，称为标准偏差，以σ表示。σ反映了测量数据偏离真实值的程度，σ越小，表示测量精度越高，因此可用σ作为评定这一测量过程精度的标准。

$RMSE = \sqrt{\frac{\sum_{i = 1}^N (y_i - \hat(y)_{i})^2}{N}}$

1.9 基尼系数-Gini

基尼系数是指国际上通用的、用以衡量一个国家或地区居民收入差距的常用指标。基尼系数介于0-1之间，基尼系数越大，表示不平等程度越高

import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
#The function used in most kernels
def gini(actual, pred, cmpcol = 0, sortcol = 1):
    assert( len(actual) == len(pred) )
    all = np.asarray(np.c_[ actual, pred, np.arange(len(actual)) ], dtype=np.float)
    all = all[ np.lexsort((all[:,2], -1*all[:,1])) ]
    totalLosses = all[:,0].sum()
    giniSum = all[:,0].cumsum().sum() / totalLosses

    giniSum -= (len(actual) + 1) / 2.
    return giniSum / len(actual)
def gini_normalized(a, p):
    return gini(a, p) / gini(a, a)
#Remove redundant calls
def ginic(actual, pred):
    actual = np.asarray(actual) #In case, someone passes Series or list
    n = len(actual)
    a_s = actual[np.argsort(pred)]
    a_c = a_s.cumsum()
    giniSum = a_c.sum() / a_s.sum() - (n + 1) / 2.0
    return giniSum / n
def gini_normalizedc(a, p):
    if p.ndim == 2:#Required for sklearn wrapper
        p = p[:,1] #If proba array contains proba for both 0 and 1 classes, just pick class 1
    return ginic(a, p) / ginic(a, a)
#XGBoost
from sklearn import metrics
def gini_xgb(preds, dtrain):
    labels = dtrain.get_label()
    gini_score = gini_normalizedc(labels, preds)
    return [('gini', gini_score)]
#LightGBM
def gini_lgb(actuals, preds):
    return 'gini', gini_normalizedc(actuals, preds), True
#SKlearn
gini_sklearn = metrics.make_scorer(gini_normalizedc, True, True)
train = pd.read_csv("../input/train.csv")
feats = [col for col in train.columns if col not in ['id','target']]
X = train[feats]
y = train['target']
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import StratifiedKFold
#Initialize random forest
rfc = RandomForestClassifier(n_estimators=100, max_depth=5, min_samples_leaf=20, max_features=0.2, n_jobs=-1)
#Stratified validation startegy
cv_1 = StratifiedKFold(n_splits=5, random_state=1).split(X, y)
#Check cross validation scores
cross_val_score(rfc, X, y, cv=cv_1, scoring=gini_sklearn, verbose=1, n_jobs=-1)

1.10 KS指标

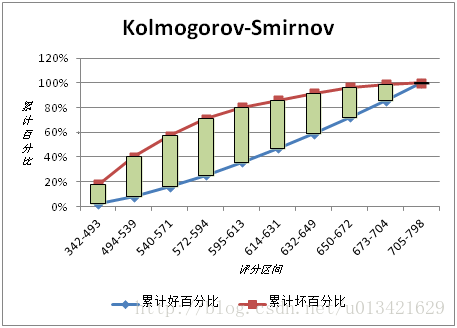
KS(Kolmogorov-Smirnov)：KS用于模型风险区分能力进行评估，指标衡量的是好坏样本累计分部之间的差值。

好坏样本累计差异越大，KS指标越大，那么模型的风险区分能力越强。

KS的计算步骤如下：

1. 计算每个评分区间的好坏账户数。
1. 计算每个评分区间的累计好账户数占总好账户数比率(good%)和累计坏账户数占总坏账户数比率(bad%)。
1. 计算每个评分区间累计坏账户占比与累计好账户占比差的绝对值（累计good%-累计bad%），然后对这些绝对值取最大值即得此评分卡的K-S值。

相关指标-python实现

# -*- coding: utf-8 -*-
import numpy as np
from sklearn.metrics import mean_squared_error

def rmse(y, yhat):
    return mean_squared_error(y, yhat) ** 0.5

def gini(y, yhat, cmpcol=0, sortcol=1):
    assert (len(y) == len(yhat))

    all = np.asarray(np.c_[y, yhat, np.arange(len(y))], dtype=np.float)
    all = all[np.lexsort((all[:, 2], -1 * all[:, 1]))]

    total_loss = all[:, 0].sum()
    sum = all[:, 0].cumsum().sum() / total_loss

    sum -= (len(y) + 1) / 2.
    return sum / len(y)

def gini_normalized(y, y_hat):
    return gini(y, y_hat) / gini(y, y)

def logloss(y, yhat):
    yhat = max(min(yhat, 1. - 10e-15), 10e-15)
    return -np.log(yhat) if y == 1. else -np.log(1. - yhat)

def rmspe(y, yhat):
    w = np.zeros(y.shape, dtype=float)
    ind = y != 0
    w[ind] = 1. / (y[ind] ** 2)
    rmspe = np.sqrt(np.mean(w * (y - yhat) ** 2))
    return rmspe

def dcg_at_k(r, k, method=1):
    r = np.asfarray(r)[:k]
    if r.size:
        if method == 0:
            return r[0] + np.sum(r[1:] / np.log2(np.arange(2, r.size + 1)))
        elif method == 1:
            return np.sum(r / np.log2(np.arange(2, r.size + 2)))
        else:
            raise ValueError('method must be 0 or 1.')
    return 0.

def ndcg_at_k(r, k=5, method=1):
    dcg_max = dcg_at_k(sorted(r, reverse=True), k, method)
    if not dcg_max:
        return 0.
    return dcg_at_k(r, k, method) / dcg_max

def ndgc_k(y, yhat, k=5):
    top = []
    for i in range(yhat.shape[0]):
        top.append(np.argsort(yhat[i])[::-1][:k])
    mat = np.reshape(np.repeat(y, np.shape(top)[1]) == np.array(top).ravel(), np.array(top).shape).astype(int)
    return np.mean(np.sum(mat / np.log2(np.arange(2, mat.shape[1] + 2)), axis=1))

def ndgc5(y, yhat):
    top = []
    for i in range(yhat.shape[0]):
        top.append(np.argsort(yhat[i])[::-1][:5])
    mat = np.reshape(np.repeat(y, np.shape(top)[1]) == np.array(top).ravel(), np.array(top).shape).astype(int)
    return np.mean(np.sum(mat / np.log2(np.arange(2, mat.shape[1] + 2)), axis=1))

def ndgc10(y, yhat):
    top = []
    for i in range(yhat.shape[0]):
        top.append(np.argsort(yhat[i])[::-1][:10])
    mat = np.reshape(np.repeat(y, np.shape(top)[1]) == np.array(top).ravel(), np.array(top).shape).astype(int)
    return np.mean(np.sum(mat / np.log2(np.arange(2, mat.shape[1] + 2)), axis=1))

def ap_at_k(y, yhat, k=5):
    if len(yhat) > k:
        yhat = yhat[:k]
    score = 0.0
    num_hits = 0.0
    for i, p in enumerate(yhat):
        if p in y and p not in yhat[:i]:
            num_hits += 1.0
            score += num_hits / (i + 1.0)
    if not y:
        return 0.0
    return score / min(len(y), k)

def map_at_k(y, yhat, k=5):
    return np.mean([ap_at_k(a, p, k) for a, p in zip(y, yhat)])

def map5(y, yhat):
    return map_at_k(y, yhat, 5)

def map10(y, yhat):
    return map_at_k(y, yhat, 10)