没有任何捷径能一步掌握数据探索.如果你想要提高模型的准确性,你会发现数据探索会极大地帮助你提高模型的准确度.
我可以很自信地说,因为我经历过很多这样的情况。
本教程帮助您理解数据挖掘的底层技术。和往常一样,我尽力用最简单的方式来解释这些概念。为了更好的理解,我举了几个例子来演示复杂的概念。
数据准备
记住一点,我们输入的数据的质量决定了我们输出的质量,因此,一旦你拿到了你的业务准备,是值得花费时间和精力在这上面的。根据我个人的经验而言,数据探索、清洗和准备能耗费整个项目的70%的时间。下面是为建立你的预测性模型所做的数据理解、清洗和准备工作:
-
变量识别
-
单变量分析
-
双变量分析
-
缺失值处理
-
异常值检测
-
变量转换
-
变量创造
最终,我们将需要在提出我们的模型之前重复前面步骤4-7多次
现在让我们从每个步骤的细节学起
变量识别
首先,搞明白自变量(predictor(input))和因变量(target(output))。下一步,清楚数据类型和变量类别.
让我们通过一个例子更清楚的理解这个步骤:
Example:-假设,我们要预测学生是否将会打板球(参考下面的数据集),这里你将需要识别自变量、因变量、变量的数据类型和变量类别(连续还是离散)
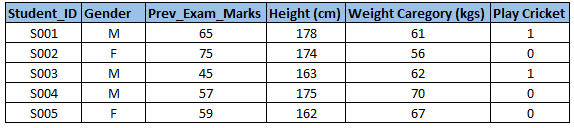
下面,变量从不同的类别区分
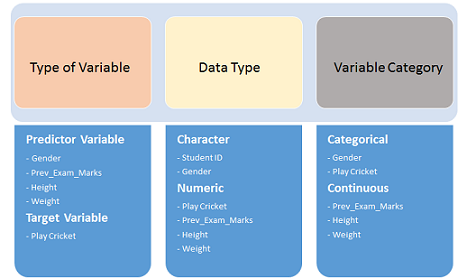
单变量分析
这个阶段,我们一个一个的探索变量,表现单变量分析的方法取决于变量类型是离散的还是连续的。分别介绍下表现离散和连续变量的技术和统计方法.
连续变量 : 对于连续变量,我们需要理解数据的中心趋势以及变量的分布.可以使用各种统计指标可视化方法进行测量,如下图所示:

Note:单变量分析也需要注意到缺失值和异常值情况。在本系列的后续部分中,我们将讨论如何处理缺失值和异常值的方法。
分类变量:-对于类别变量,我们将使用频率表来理解每个类别变量的分布。我们可以看到每一个类别的数值出现百分比。针对每一个类别变量,可以使用计数或者百分比来度量。也可以使用柱状图可视化每一个类别变量。
双变量分析
双变量分析主要发现两个变量之间的关系。在这里,我们寻找在一个预定义的显著水平上的变量之间的关联和分离。我们可以对任何分类和连续变量的组合进行双变量分析。比如:分类和分类,分类和连续,连续和连续。在分析过程中使用不同的方法来处理这些组合。
让我们详细了解每一种组合:
Continuous & Continuous: 可以使用散点图在两个连续变量之间进行双变量分析,这是找出两个变量之间关系的一个好方法,散点图表明了两个变量之间的关系,线性关系还是非线性关系.

散点图虽然可以找到两个变量之间的关系,但是无法衡量两个变量之间的关系强度,可以使用相关性度量方法表示两个变量之间的关系强度,一般相关性值只要在-1和1之间变化.
- -1:完全负线性相关
- +1:完全正线性相关
- 0: 不相关
相关性可以用以下公式推导出来:
Correlation = Covariance(X,Y) / SQRT( Var(X)* Var(Y))
各种工都具有识别变量之间的相关性的功能。在Excel中,函数CORREL()用于返回两个变量之间的相关性,SAS使用过程PROC CORR来识别相关性。这些函数返回Pearson相关值来确定两个变量之间的关系:
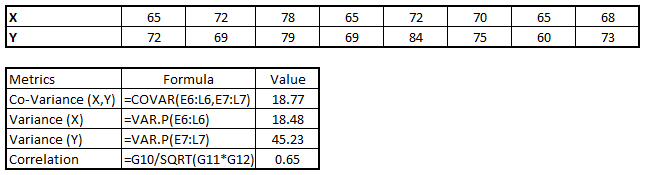
Categorical & Categorical: 对于离散与离散变量之间的双变量分析,可以使用下面方法:
- 1.Two-way table: 我们可以通过count和count%的双向表来分析关系。行表示一个变量的类别,列表示另一个变量的类别。双向表显示了每个行和列类别组合中的值的百分比或count%。
- 2.Stacked Column Chart: 可以说是双向表的可视化展示
- 3.Chi-Square Test: 卡方检验主要是衡量两个变量之间关系的重要程度,两个变量之间的偏离程度决定了卡方值的大小,卡方值越大,越不符合;卡方值越小,偏差越小,越趋于符合,若两个值完全相等时,卡方值就为0,给定自由度下返回卡方分布的概率;当概率为0时候,表明两个变量相关;当概率为1是,表明两个变量相互独立.当概率小于0.05时,表明两个类别变量在95%置信水平上是相关的.两个分类变量独立检验的卡方检验统计量为:
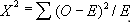
其中O是观测值的频率,E是期望值的频率,计算方式为:
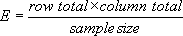
Categorical & Continuous: 探索离散变量跟连续变量之间的关系,可以绘制箱线图进行可视化,如果数值较小,则无统计意义,为了查看变量之间的统计意义,可以使用Z-test, T-test,或ANOVA等方法.
Z-Test/ T-Test: 平均值差异性检验的方法。它是用标准正态分布的理论来推断差异发生的概率,从而比较两个平均数的差异是否显著.

当Z值越小,说明两个平均值的差异越大,T检验跟Z检验相似.

ANOVA: 方差分析,用于两个及两个以上样本均数差别的显著性检验。 由于各种因素的影响,研究所得的数据呈现波动状。造成波动的原因可分成两类,一是不可控的随机因素,另一是研究中施加的对结果形成影响的可控因素。
Example: 假设,我们想测试五个不同锻炼的效果。为此,我们招募了20名男性,并将一种锻炼方式分配给4名男性(5组)。几周之后,记录他们的体重。我们需要弄清楚这些锻炼对他们的影响是否显著不同。这可以通过比较5组中每4人的重量来完成。
在此之前,我们已经了解了数据挖掘的前三个阶段,即变量识别、单变量和双变量分析。我们还研究了各种统计和可视化方法来确定变量之间的关系。
现在,我们来看看缺失值处理的方法。更重要的是,我们还将研究为什么我们的数据中会出现缺失值,以及为什么要对它们进行处理。
缺失值处理
若在训练数据集中存在缺失值,若不处理,则会影响到模型的性能或者产生一个有偏差的模型,因为我们没有正确地分析缺失变量与其他变量的关系,有可能会导致错误的预测或者分类.
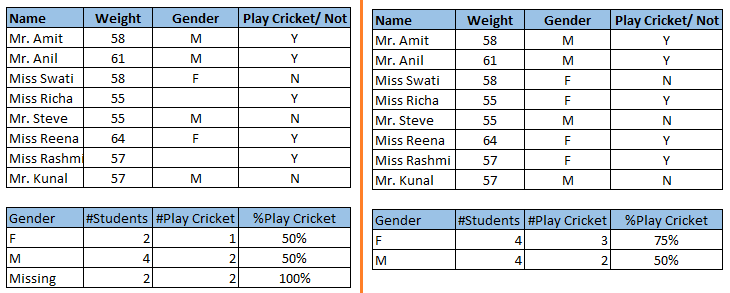
上图中:左图,我们没有对缺失值进行处理。可以看到男性大板球的概率要高于女性。另一方面,右图中,对缺失值(基于性别)的处理后的数据,我们可以看到,与男性相比,女性更有可能打板球。
可以看到在数据集中处理缺失值的重要性。现在,让我们找出这些缺失值出现的原因。它们可能发生于:
-
1.数据提取:可能发生于提取过程中。在这种情况下,我们应该验证下数据的正确性。数据提取阶段的错误通常很容易找到,也可以很容易地纠正。
-
2.数据收集:发生在数据收集的时候,很难纠正。
-
2.1完全随机丢失:对于所有数据而言,缺失变量的概率相同.
-
2.2随机缺失:对所有数据而言,缺失变量概率不一样,比如女性的缺失概率比男性高.
-
2.3依赖于未观察到的预测值:当缺失值不是随机的,并且与未观察到的输入变量相关,例如:在医学研究中,如果某一特定的诊断引起不适,那么从研究中退出的机会就会增加。这个缺失值不是随机的,除非我们将“不适”作为所有患者的输入变量。
-
2.4依赖于缺失值本身:当缺失值的概率与缺失值本身直接相关,例如:收入较高或收入较低的人很可能对自己的收入不作反应。
-
如何处理
- 删除:它有两种类型:
List Wise Deletion和Pair Wise Deletion。
List Wise Deletion: 如果一个样本出现缺失值,则直接删除该样本.虽然简单,但是可能因为减少样本量造成模型的不稳定.
Pair Wise Deletio: 对感兴趣的变量进行分析。虽然保留了许多样本,但是对不同的变量使用不同的样本大小。
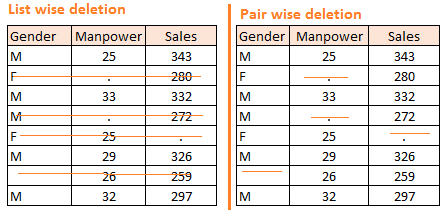
- 填充: 使用均值/众数/中位数等进行填充。主要分为两种模式:
- 直接使用全局数据的均值/众数/中位数等直接进行填充.
- 使用相似的变量的统计特征进行填充
- 模型预测: 使用模型预测值进行填充是一种较为复杂的方法.一般将数据集分成两组:一组没有缺失值,另一组为缺失值。第一个数据集作为模型的训练数据集,而包含缺少值的第二个数据集是测试数据集,缺失值的变量被当作目标变量。接下来,我们建立一个模型,根据训练数据集的其他属性来预测目标变量,并填充测试数据的缺失值。我们可以使用回归、方差分析、逻辑回归和各种建模技术来实现这一点。这种方法有两个缺点:
- 模型估计的值通常比真正的值表现得更好。
- 如果数据集和缺少值的属性之间没有关系,那么模型就不会精确地估计缺失值。
KNN方法: 通过相似的样本值来填充缺失值。利用距离函数确定两个属性的相似度。它也有一定的优点和缺点。
-
优点: k近邻可以预测定性和定量属性; 不需要为每个具有缺失数据的属性创建预测模型;具有多个缺失值的属性可以很容易地处理;将数据的相关结构考虑在内。
-
缺点: :KNN算法在大型数据分析中非常耗时。它在所有数据集中搜索最相似的实例;k值的选择非常关键。较高的k值将包含显著的属性,而较低的k值意味着缺少重要的属性。
处理缺失值后,接下来需要处理离群值。通常,我们在构建模型时往往忽略了异常值。异常值会使你的数据不平衡,并且会降低模型的准确性。
异常值处理
在对数据进行分析时,需要密切关注异常值,否则可能导致严重错误的估计。简单地说,异常值往往偏离样本,用图可视化的话,一般异常值都是一些孤立的点。
举个例子,我们做客户分析,发现客户的平均年收入是80万美元。但是,有两个客户的年收入是4美元和420万美元。这两个客户的年收入比其他人高得多。显然这两个客户的年收入将被视为异常值。
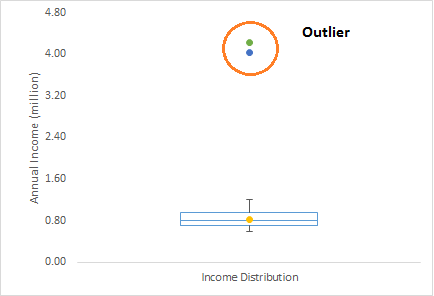
异常值有两种类型:单变量和多变量。上面,我们讨论了单变量离群的例子,当我们观察单个变量的分布时,就可以发现这些异常值。在n维空间中,为了发现多变量的异常值,你必须考虑多变量的分布。
让我们以一个例子来理解这一点。观察身高和体重之间的关系。使用单变量和双变量分布分析身高跟体重。由箱线图可以看到不存在异常值(超过1.5*IQR,最常用的方法)。再看看散点图,很明显存在异常值.
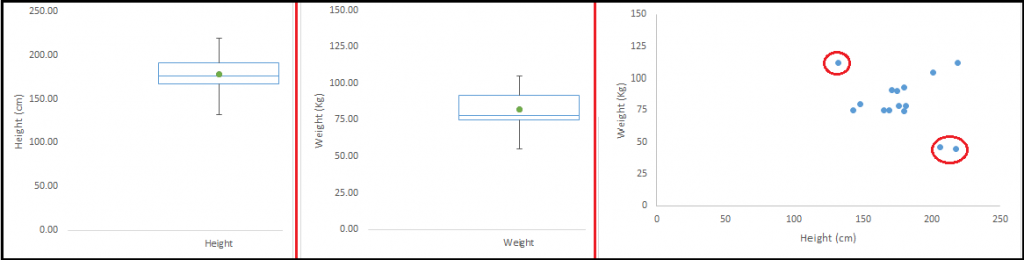
异常值的存在会极大地影响到数据分析和统计建模的结果。若数据集中存在异常值有,则:
-
增加了误差方差,降低了统计测试的能力。
-
如果异常值是非随机分布的,会降低正态性。
-
可能会造成偏差或影响估计。
-
影响回归、方差分析和其他统计模型假设的基本假设。
简单的以一个例子说明,有无异常值的数据情况.
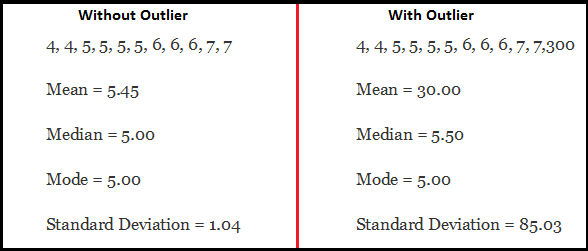
如图所示,具有异常值的数据集很明显平均值和标准偏差存在问题。左图平均值是5,右图平均值是45,随着离群值的增加,平均值上升到30,这将完全改变估计。
如何处理
最常用的检测异常值的方法是可视化。我们使用各种可视化方法,如箱形图、直方图、散点图(上图,我们用了箱线图和散点图来可视化)。一些分析师也用不同的经验法则来检测异常值。一般常用的是:
-
超出-1.5 x IQR到1.5 x IQR的范围的值认为是异常值。
-
超出5%和95%的值都认为是异常值。
-
超过平均值的3倍标准偏差则认为是异常值。
-
异常值检测仅仅是对有影响的数据点进行数据检查的一种特殊情况,它还取决于业务理解。
-
双变量和多变量异常值检测还可以通过距离等指标来衡量。像Mahalanobis ’ distance和Cook ’ s D指标经常被用来检测异常值。
大多数处理异常值的方法类似于缺失值的方法,比如删除,变换,分箱,将它们作为一个单独的组,估算值和其他统计方法。我们将讨论用于处理异常值的常用技术:
删除:如果由于数据输入错误、数据处理错误等造成异常值,可以直接删除异常值。还可以在两端进行修剪以去除异常值。
转换和分箱:转换变量也可以消除异常值。比如数值的取对数(log)也可以消除两端的影响。分箱也是变量转换的一种形式。由于进行变量的分箱,所以决策树算法也可以很好地处理异常值。还可以针对不同的数值分配不同权重
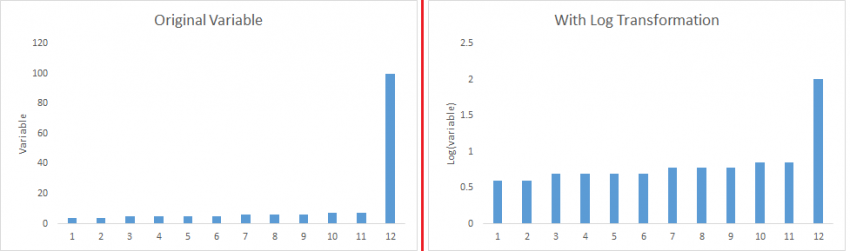
填充: 像处理缺失值一样,我们同样也可以使用数据的中位数/众数/均值等对异常值进行替换处理.
分割: 如果存在大量的异常值,则可以将异常值作为单独的一个组进行分析.
在此之前,我们已经了解了数据挖掘的步骤、缺失值的处理以及异常值检测和处理的技术。这三个阶段将使您的原始数据在信息可用性和准确性方面更好。现在让我们进入数据探索的最后阶段-特征工程。
特征工程
特征工程是从现有数据中提取更多信息的科学(和艺术)。没有添加任何新数据,但是实际上您已经在使数据变得更有用了。
举个例子,假设你正试图预测一个基于日期的购物中心的人流量。如果您尝试直接使用日期,您可能无法从数据中提取有意义的见解。因为人流量的大小更多的受周几的影响而不是一个月的第几天。而关于周几的信息是隐含在你的数据中。你需要挖掘出来,让你的模型更好。
这是一种从数据中提取信息的操作,称为特征工程。
一旦你完成了数据挖掘中的前5个步骤——变量识别、单变量、双变量分析、缺失值处理和异常值处理,你就会执行特征工程。特征工程本身可以分为两步:
-
变量变换。
-
变量/特征功能。
这两种技术在数据探索中是至关重要的,对预测能力有显著的影响。让我们更详细地了解这一步。
变量转换
在数据建模中,转换是指用函数替换变量。例如,用方根/立方根或对数替换变量x是一个变换。换句话说,转换是一个过程,它改变变量与其他变量的分布或关系。
常见的变量变换方法:
-
当我们想要改变变量的大小时可以对变量进行标准化,以便更好地理解。如果数据的各个变量大小不同时,有必要进行标准化处理,这个转换不会改变变量的分布。
-
当我们想把复杂的非线性关系转化成线性关系时。与非线性或曲线关系相比,变量之间存在线性关系更容易理解。转换帮助我们将非线性关系转换成线性关系。散点图可以用来发现两个连续变量之间的关系。这些转换还可以改进预测。
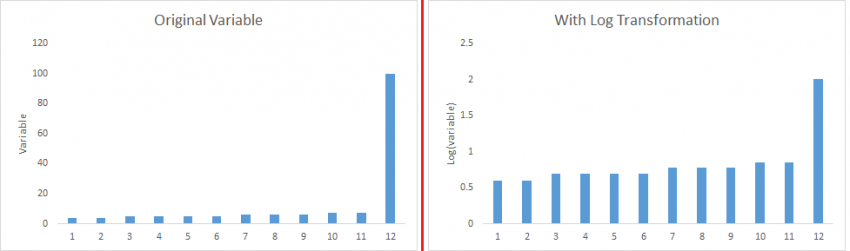
log转换是常用的转换技术之一。
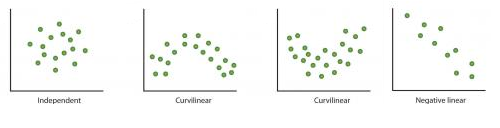
- 对称分布优于有偏分布,因为它更容易解释和产生推论。一些建模技术要求变量分布满足正态分布。因此,当我们有一个偏态分布时,我们可以使用转换来降低有偏的影响。对于右偏分布,我们取
square/cube root或log,对于左偏态,我们取square/cube或exp。
- 分箱也是变换转换的一种常用方法,比如对于年龄字段,一般对其进行分箱处理。
有各种方法用于转换变量。如前所述,其中一些包括平方根、立方根、对数、分箱、倒数等。让我们详细了解这些方法。
-
log: 取对数是一种常用的变换方法,用来改变分布曲线上变量的分布形状。它通常用于减小变量的右偏度。但是,它也不能被应用到零或负值。
-
Square / Cube root: 对变量取方根或立方根会对变量分布有良好的影响。然而,它并不像对数变换那样重要。立方根有它自己的优势。它可以应用于负值,包括零。平方根可以应用于正值,包括零。
-
Binning:用于对变量进行分箱。常用频率或者百分比进行分箱。往往分箱的结果一部分取决于业务理解,一部分取决数据本身
特征构造
特性/变量构造是一个基于现有变量生成新的变量/特性的过程。例如,我们将日期(dd-mm-yy)作为数据集中的输入变量,我们可以生成新的变量,比如日期、月、年、周、工作日,这些变量可能与目标变量有更好的关系。此步骤用于强调变量中隐藏的关系:
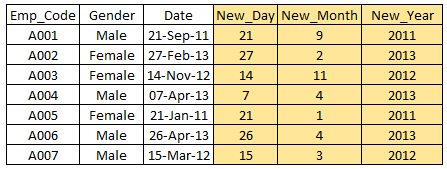
有各种各样的技术来创建新特征。让我们来看看一些常用的方法:
-
衍生变量: 从现有变量中创建新变量。让我们通过“泰坦尼克号- Kaggle竞赛”来看看它。在这个数据集中,年龄变量有缺失值。为了预测缺失值,我们使用了称呼(Master, Mr, Miss, Mrs)作为一个新变量。我们如何决定构造哪些变量?坦白地说,这取决于对分析师的商业理解,他的好奇心以及他可能对这个问题的假设。比如取变量的log,binning变量和其他变量变换的方法也可以用来创建新的变量。
-
哑变量:哑变量是将分类变量转换为数值变量最常见的应用之一。通过将类别变量映射为0值或者1值。
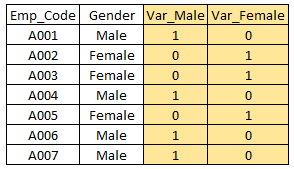
原文地址: https://www.analyticsvidhya.com/blog/2016/01/guide-data-exploration/