LoRA是微软研究员引入的一项新技术,主要用于处理大模型微调的问题。目前超过数十亿以上参数的具有强能力的大模型 (例如 GPT-3) 通常在为了适应其下游任务的微调中会呈现出巨大开销。 LoRA 建议冻结预训练模型的权重并在每个 Transformer 块中注入可训练层 (秩-分解矩阵)。因为不需要为大多数模型权重计算梯度,所以大大减少了需要训练参数的数量并且降低了 GPU 的内存要求。研究人员发现,通过聚焦大模型的 Transformer 注意力块,使用 LoRA 进行的微调质量与全模型微调相当,同时速度更快且需要更少的计算。
介绍
LoRA的主要思想是将预训练模型权重冻结,并将可训练的秩分解矩阵注入Transformer架构的每一层,大大减少了下游任务的可训练参数数量。具体来说,它将原始矩阵分解为两个矩阵的乘积,其中一个矩阵的秩比另一个矩阵的秩低。这时只需要运用低秩矩阵来进行运算,这样,可以减少模型参数数量,提高训练吞吐量,并且在模型质量上表现出色,且不会增加推理延迟。
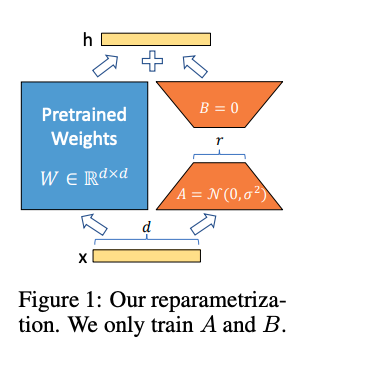
如上图所示们对于某个线性层而言,左边是模型原有的参数,在训练过程中是冻结不变的,右边是LoRA方法增加的低秩分解矩阵。训练过程中,优化器只优化右边这一部分的参数,两边的矩阵会共用一个模型的输入,分别进行计算,最后将两边的计算结果相加作为模块的输出。不同于之前的参数高效微调的Adapter,Adapter是在模块的后面接上一个MLP,对模块的计算结果进行一个后处理,而LoRA是和模块的计算并行的去做一个MLP,和原来的模块共用一个输入。
方法
LoRA 是Parameter Efficient 的方法之一。已有研究表明了过度参数化的模型其实是位于一个低的内在维度上,所以作者假设在模型适应过程中的权重变化也具有较低的“内在等级”。LoRA的主要方法为冻结一个预训练模型的矩阵参数,并选择用A和B矩阵来替代,在下游任务时只更新A和B,即在原始PLM旁边增加一个旁路,做一个降维再升维的操作,来模拟所谓的intrinsic rank。训练的时候固定PLM的参数,只训练降维矩阵A与升维矩阵B。而模型的输入输出维度不变,输出时将BA与PLM的参数叠加。用随机高斯分布初始化A,用0矩阵初始化B,保证训练的开始此旁路矩阵依然是0矩阵。
具体来看,假设预训练的权重矩阵为,它的更新可表示为:
其中。在训练过程中, 被冻结,不进行梯度更新,而A和B包含可训练的参数。
理论上LoRA可以支持任何线性层,包括Transformer中的4个Attention矩阵和2个Feed-Forward中的矩阵,论文旨在Attention上做了实验,它限制总参数量不变的情况下观察是在Attention其中一个矩阵上,放一个更高秩的LoRA,还是在多个Attention的矩阵上,分别放置低秩一点的LoRA效果好?结论是把秩分散到多个矩阵上,效果会优于集中在单个上的效果。至于在一般任务上很小的秩就可以和很大秩的效果,这也证明了作者一开始做出的改变量低秩的假设。
实验
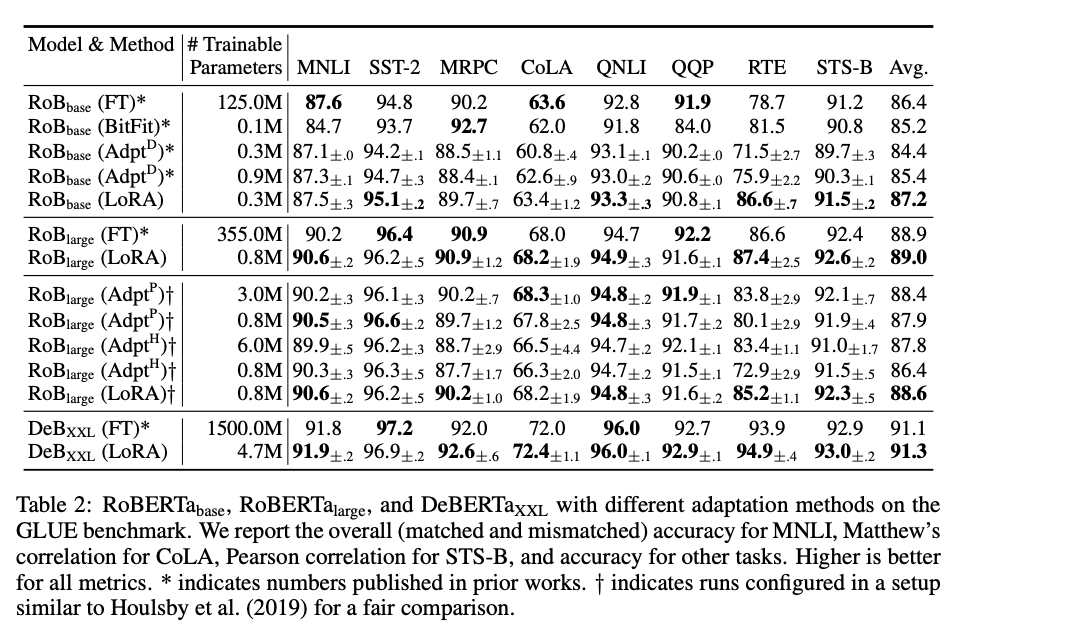
从上表,可知:
- 参数量较全参数微调显著降低,和现有参数高效微调方法持平或更低
- 性能优于其他参数高效微调方法,和全参数微调几乎持平甚至更高
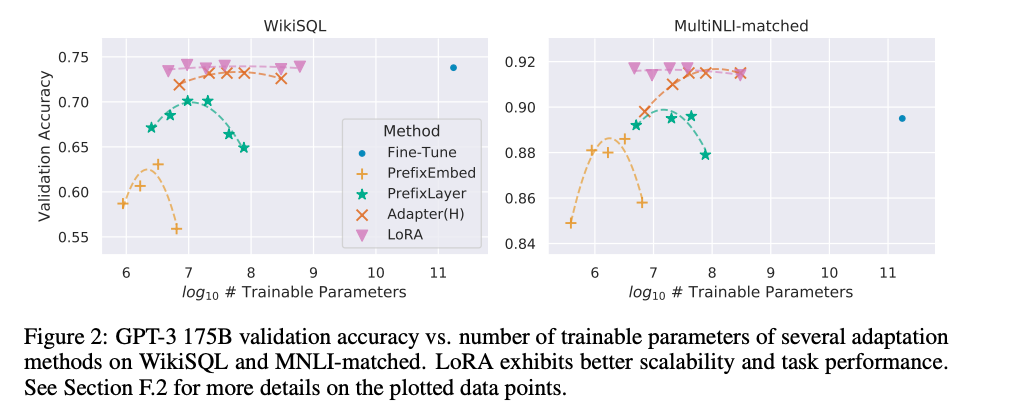
从上图可知,相比其他的参数高效微调方法,增大参数量收敛性一直比较稳定
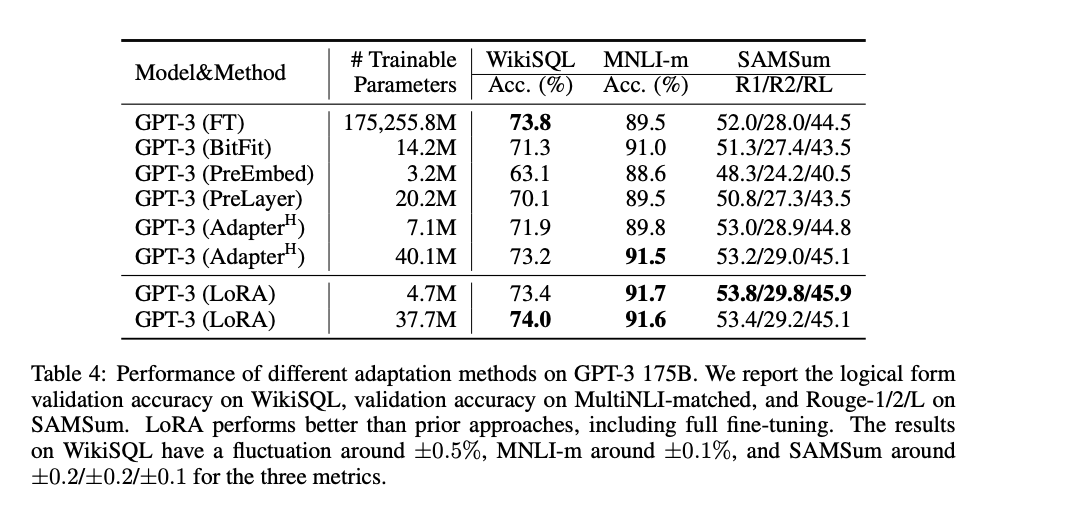
从上表可知,经过LoRA方法,最终效果持平甚至超过 GPT-3 全参数微调。
总结
总的来说,LoRA详细过程如下:
- 在原模型旁边增加一个旁路, 通过低秩分解 (先降维再升维) 来模拟参数的更新量;
- 训练时, 原模型固定, 只训练降维矩阵A和升维矩阵B;
- 推理时, 可将BA加到原参数上, 不引入额外的推理延迟;
- 初始化, A采用高斯分布初始化, B初始化为全 0 , 保证训练开始时旁路为 0 矩阵;
- 可插拔式的切换任务, 当前任务W0+B1A1, 将lora部分减掉, 换成B2A2, 即可实现任务切换;
- 秩的选取:对于一般的任务, rank 足矣, 而对于一些领域差距比较大的任务可能需要更大的rank。