目前在自然语言处理领域,Transformer的编码能力超越了RNN,但是对长距离依赖的建模能力仍然不足。在基于LSTM的模型中,为了建模长距离依赖,提出了门控机制和梯度裁剪,目前可以编码的最长距离在200左右。在基于Transformer的模型中,允许词之间直接self-attention,能够更好地捕获长期依赖关系,但是还是有限制,本文将主要介绍Transformer-XL,并基于PyTorch框架从头实现Transformer-XL。
原始Transformer
细想一下,BERT在应用Transformer时,有一个参数sequence length,也就是BERT在训练和预测时,每次接受的输入是固定长度的。那么,怎么输入语料进行训练时最理想的呢?当然是将一个完整的段落一次性输入,进行特征提取了。但是现实是残酷的,这么大的Transformer,内存是消耗不起的。所以现有的做法是,对段落按照segment进行分隔。在训练时:
- 当输入segment序列比sequence length短时,就做padding。
- 当输入segment序列比sequence length长时就做切割。
这种做法显然是一种权宜之计,它有这么两个缺点:
-
长句子切割必然会造成语义的残破,不利于模型的训练。
-
segment的切割没有考虑语义,也就是模型在训练当前segment时拿不到前面时刻segment的信息,造成了语义的分隔。
那么,该如何解决上述问题呢?围绕建模长距离依赖,提出Transformer-XL【XL是extra long的意思】。
Transformer-XL
我们先想一下,如果要我们自己来解决Transformer上面的问题,会怎么处理呢?
熟悉NLP的同学,可能会想到RNN。在RNN中,为了获取序列中的历史记忆,采用了Recurrence机制,在计算该时刻的状态时,引入前一时刻的状态作为输入。那对Transformer来说,在计算当前序列的隐藏状态时,引入前一个序列的隐藏状态信息不就可以解决上面的问题了吗?
事情真的有这么简单吗?其实,基本上也就是这么简单,不过Transformer-XL在引入时做了一些巧妙的设计。下面我们看看,Transformer-XL是如何引入这种Recurrence机制来解决上述问题的。

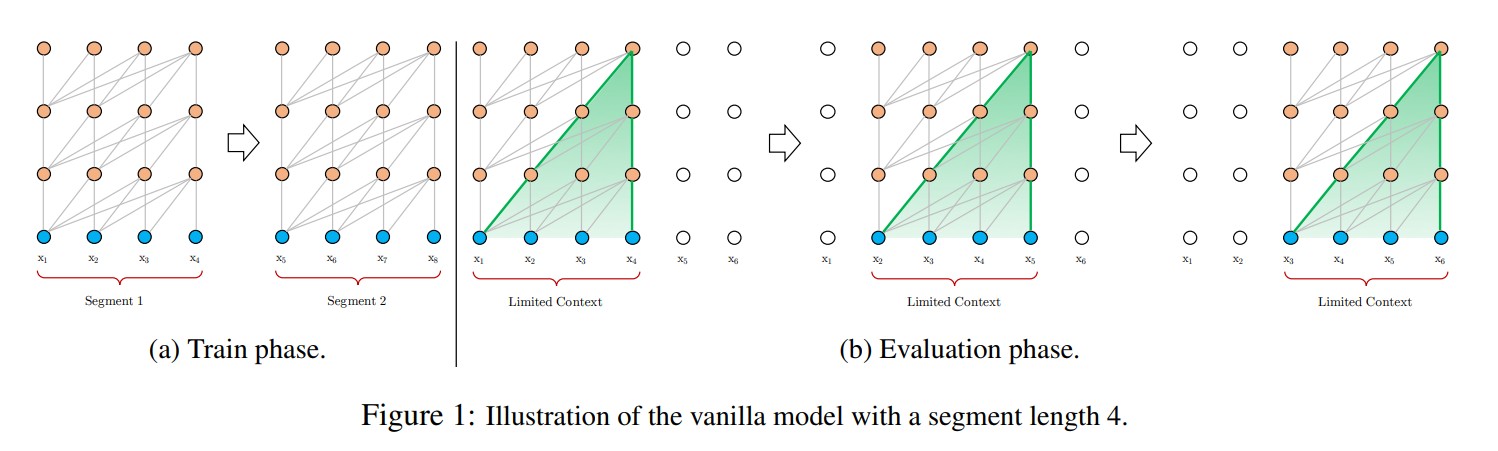
上图是传统的Transformer在训练和评估阶段采用的语料输入策略。在训练时,将整个语料库分割成可管理的大小的更短的片段,在每个片段中训练模型,忽略来自前一段的所有上下文信息;在评估阶段,传统的Transformer模型在每个步骤都消耗与训练期间相同长度的一个segment。然后,在下一步中,这个segment向右移动一个位置,并从头开始处理,只在最后一个位置进行一次预测。
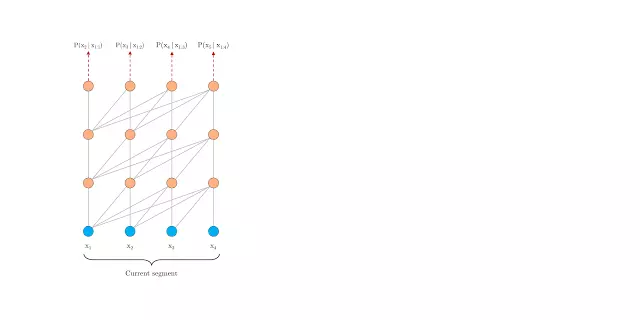
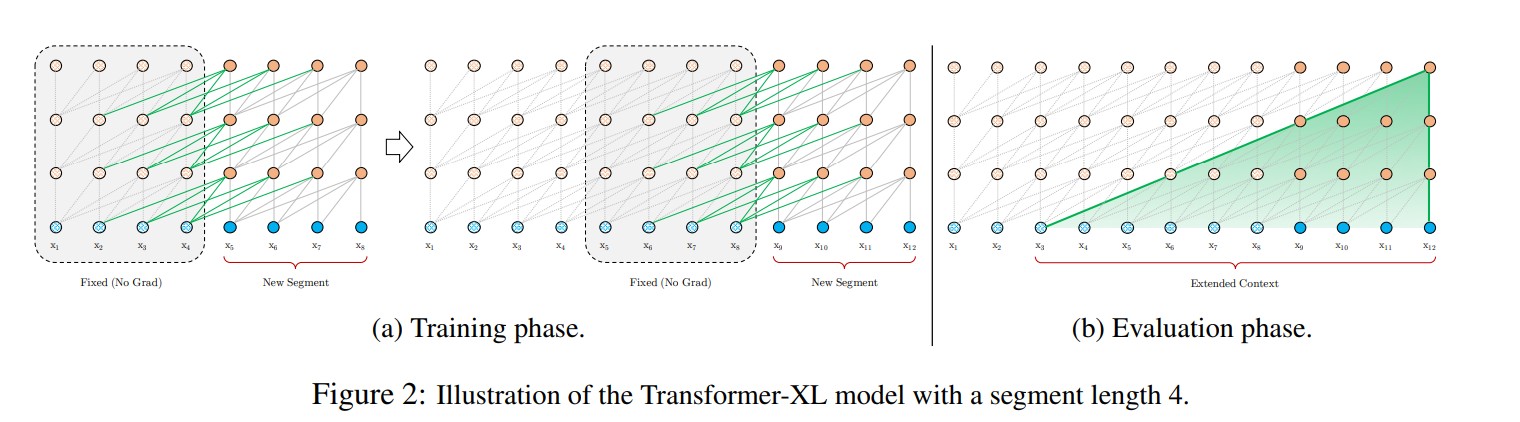
如上图所示,Transformer-XL采用了不同的策略,在训练过程中,对上一个segment计算的隐藏状态序列进行固定和缓存,并在模型处理下一个新的segment时对其进行利用。在评估阶段,可以重用前面部分的表示,而不是像传统模型那样从头开始计算,这样可以提高速度。
总的来说,相比Transformer,改进如下:
-
片段级别的循环机制:增加Transformer处理文本的长度,而且解决文本碎片(指的是之前的Transformer最大处理长度为定长sequence length,超过sequence length则会截断,这样导致截断处文本信息断裂,连接不上上下文)的问题。相当于滑窗,窗口大小为sequence length。
-
相对位置编码:解决在不同片段中相同token,绝对位置编码可能相同,无法区分的问题。采用相对距离的方式得到相应的位置编码。
Recurrence机制
事实上,问题的关键在于,在计算当前序列当前层的隐藏状态时,如何引入前一个序列上一层的隐藏状态。Transformer-XL的做法很简单,就是按照序列长度的维度将他们concate起来。如下的公式所示:
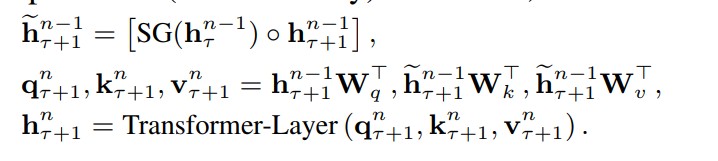
其中:
-
是一个的矩阵,表示的是第个输入序列的第层的隐藏层的状态。表示序列长度,表示嵌入维度。
-
SG(.)表示的Stop Gradient,这非常重要,避免了RNN会出现的一系列问题。
从上述公式可以看出,Transformer-XL与传统的Transformer的差异主要在于隐藏层输入K和V的差异。Transformer-XL中引入了上一个序列前一个隐藏层的值,将他们concatenate起来,计算新的K和V。
具体以下图进行详细说明;
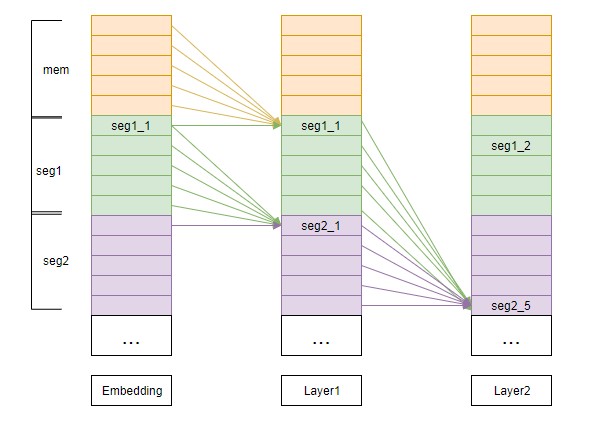
所谓循环机制(其实就是滑窗),就是要重用之前的状态(上图中,橙色部分为初始的记忆单元memory,绿色部分表示segment)。比如在Layer1中,要计算第1个片段第1个位置seg1_1的结果,需要用到前一层的 “记忆单元(Embedding中的mem)和 seg1_1”。再比如在计算Layer1中seg2_1时,mem变成了Embedding中的seg1。就是说,窗口滑动是以片段为单位的。图中,箭头部分,表示当前需要计算的内容的attend来源。橙色箭头表示来自上一层的mem,绿色箭头表示来自上一层的对应的位置。
在计算attention时(比如Layer1的seg1_1,Q为Embedding的seg1_1,K=V为embedding中的mem+seg1_1),先计算 attn_weight =$ softmax(QK^T)$ ,表示要产生Layer1中seg1_1的attention,每个V要贡献的权重;再计算attn_weight$ * V$ ,表示V加权求和的结果。需要注意的是,在计算反向传播时,mem部分是不进行梯度更新的。此外,这里可以很明显的看出与RNN等循环网络,“循环”的不同之处在于,RNN是在同一层传递的( 用到 及之前的记忆),Transformer-XL是在不同层之间传递的( 用到 及以前的记忆)。
Relative Positional Encodings
在传统的Transformer中,输入序列中的位置信息是怎么表示的?通过POS函数生成,它是位置和维度的函数,也就是不同输入segment在相同绝对位置中的位置表示是相同的。在传统的Transformer中,每个segment之间的表示是没有关联的,这当然就没有问题。但是在Transformer-XL中,因为引入了前一时刻segment的信息,就需要对不同时刻,同样是第个的词进行区分。
Transformer-XL引入了一种Relative Positional Encodings机制,会根据词之间的相对距离而非像传统的Transformer中的绝对位置进行编码。
在传统的Transformer中,计算和键之间的attention分数的方式为
展开就是:
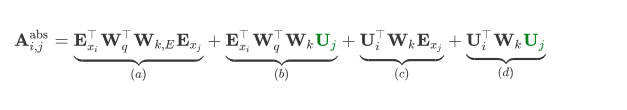
其中:
- 是词的embedding
- 是词的embedding
- 和 是位置向量。
在Transformer-XL中,对上述的attention计算方式进行了变换,转为相对位置的计算,而且不仅仅在第一层这么计算,在每一层都是这样计算。
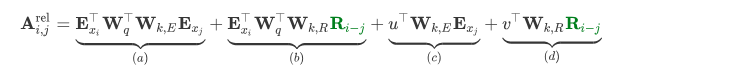
对比来看,主要有三点变化:
-
在b和d这两项中,将所有绝对位置向量,都转为相对位置向量,与Transformer一样,这是一个固定的编码向量,不需要学习。
-
在c这一项中,将查询的向量转为一个需要学习的参数向量,因为在考虑相对位置的时候,不需要query的绝对位置,因此对于任意的,都可以采用同样的向量。同理,在d这一项中,也将query的向量转为另一个需要学习的参数向量v。
-
将K的权重变换矩阵转为 和,分别作为content-based key vectors和location-based key vectors。
四部分分别对应为:
- 基于内容的“寻址”,即没有添加原始位置编码的原始分数。
- 基于内容的位置偏置,即相对于当前内容的位置偏差。
- 全局的内容偏置,用于衡量key的重要性。
- 全局的位置偏置,根据query和key之间的距离调整重要性。
总的来说,Relative Positional Encodings就是在计算attention分数时,用相对位置编码来代替原来的绝对位置编码和。并且学习了相对位置v和u用来调整不同距离和不同嵌入的得分。
计算公式
结合上面两个创新点,将Transformer-XL模型的整体计算公式整理如下,这里考虑一个N层的只有一个注意力头的模型:

其中,代表第几段,代表第几层,定义为第的词向量序列。值得一提的是,计算矩阵的时候,需要对所有的计算,如果直接按照公式计算的话,计算时间是 ,而实际上的范围只从0 ~ length,因此可以先计算好这length个向量,然后在实际计算矩阵时直接取用即可。
具体的,设和分别为memory和当前段序列的长度,则的范围也就为0 ~ M + L - 1。下面的Q矩阵中的每一行都代表着中一个的可能性,即。
则对于上面公式中的(b)项,即,其构成的所有可能向量的矩阵为矩阵,其形状为L * (M + L)。
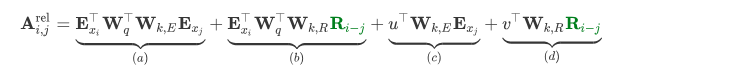
从上式中,这是我们最终需要的(b)项的attention结果。

我们进一步定义
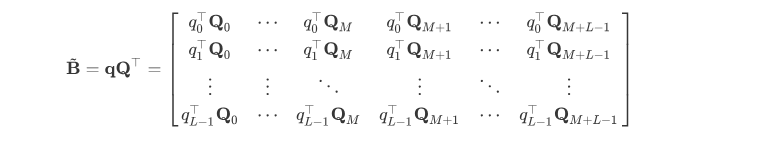
可见,需要的B矩阵的每一行只是的向左shift而已。因此,可以直接利用矩阵乘法计算即可。设的维度为,的维度为,矩阵的维度为,则直接计算矩阵B的时间复杂度为,而计算的时间复杂度为,计算量明显不是一个量级(后者要快很多)。
我们以一个二维矩阵进行说明:
1 | x = torch.linspace(1, 12, 12).view(3,4) |
1 | zero_pad = torch.zeros((x.size(0), 1)) |
总的来说Transformer-XL对Transformer进行了一些调整,试图解决一些问题。按照论文的描述,Transformer-XL学习的依赖关系比RNN长80%,比传统Transformer长450%,在短序列和长序列上都获得了更好的性能,并且在评估阶段比传统Transformer快1800+倍。
实验
接下来,我们将使用PyTorch框架从头实现Transformer-XL。真正理解某个模型的最好方法是从头开始构建。
概述
由于Transformer-XL涉及到Transformer,因此让我们来回顾一下最初的Transformer结构。总体而言,Transformer结构是由多个MultiHeadAttention层堆叠在一起,并包含前馈层、残差层和层标准化层。如下图所示:
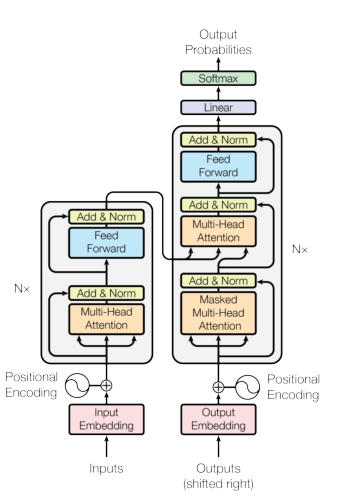
MultiHeadAttention层由多个attention head组成。每个attention head对其输入应用一个线性变换,并使用keys和querys计算其输入values上的attention。如下图所示:
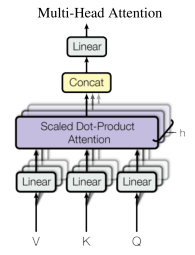
这种方法无法步抓到位置信息,因此Transformer将表示输入位置的embeddings与词embeddings进行相加。
现在,我们来看看Transformer-XL。为了更全面地了解整个数据流,看一下Transformer-XL的前向传递的简化版本:
1 | def forward(self, input_): |
其中:
-
memory: 这是Transformer XL的独特之处。正确地处理memory是使Transformer-XL正确运行的关键点之一。
-
layer: 这是Transformer-XL的核心部分。虽然这与MultiheadAttention层基本相同,但是有几个关键的变化,比如相对位置编码。
接下来,我们将详细的实现每一个部分。
单Attention Head
我们将首先在一个MultiHeadAttention 层中实现一个attention head。以第一层为例,假设该层的收入为一个shape为(seq=7, batch_size=3, embedding_dim=32)的word embeddings。注意,Transformer-XL并不向输入添加位置embedding。
1 | seq, batch_size, embedding_dim = 7, 3, 32 |
在Transformer-XL中,我们需要缓存之前的序列的输出。在第一层中,之前的序列输出定义为词embeddings。
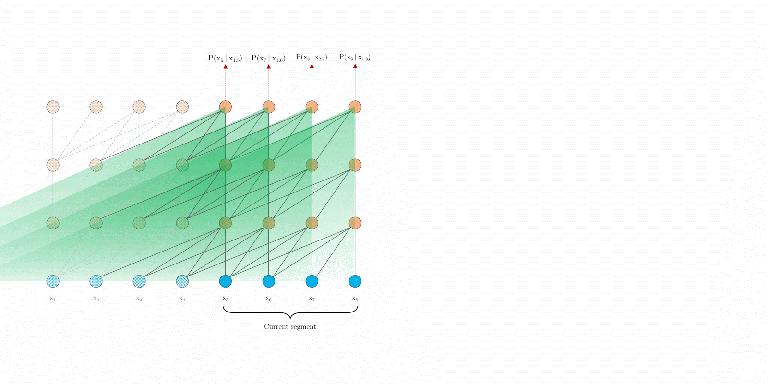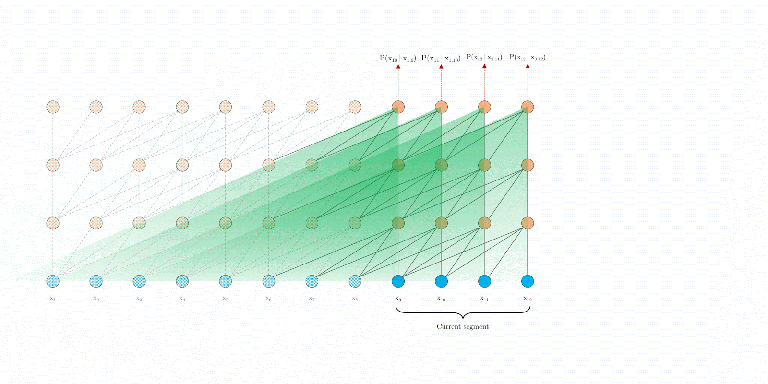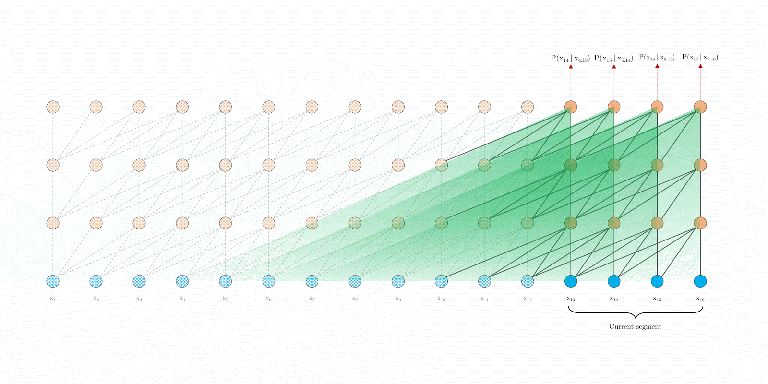
另外假设之前的序列长度为prev_seq=6,则:
1 | prev_seq = 6 |
每个attention head以keys、queries和values作为输入。并进行下面的处理过程::
-
对每个keys、queries和、values进行不同的线性变换。
-
计算每个values的 attention scores。
-
对于每个query,计算values的attention-weighted sum。
-
进行残差连接和层标准化。
我们从线性变换开始。
1 | inner_dim = 17 # this will be the internal dimension |
从Transformer-XL计算公式可知,keys和values与正常Transformer中的keys,values是不一样的。根据公式,将memory和输入在序列长度纬度进行拼接,并作为keys/values的输入。需要注意的是,query是不做该变化的,因为每个query表示一个我们想要预测的单词。
1 | word_embs_w_memory = torch.cat([memory, word_embs], dim=0) |
接下来,我们类似正常的Transformer一样计算scaled dot product attention。scaled dot product attention通过计算query和key向量之间的点积作为attention score。为了防止values随着向量维数的增加而太大,我们将原始attention score除以embedding size的平方根。
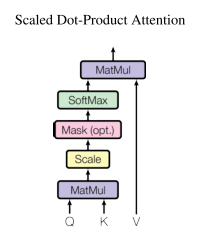
我们将在这里使用einsum符号进行编写,如果你不熟悉einsum的话,可以点击该教程连接。简而言之,einsum表示输入和输出的形状,使用一个字母表示每个维度。下面,输入的形状是’ (i, b, d) ‘和’ (j, b, d) ‘,输出的形状是’ (i, j, b) ',其中相同的字母表示相同的大小。einsum是通过对具有相同字符的维度进行点积来计算的。
1 | content_attn = torch.einsum("ibd,jbd->ijb", q_tfmd, k_tfmd) / (embedding_dim ** 0.5) # scale |
注意,我们没有使用softmax激活函数,因为还要计算相对位置编码。
相对位置编码
Transformer-XL中的一个关键点是相对位置编码。Transformer-XL计算一个表示任意两个token之间距离的embeddings,而不是使用每个token的绝对位置embeddings。
向量和向量计算公式如下:
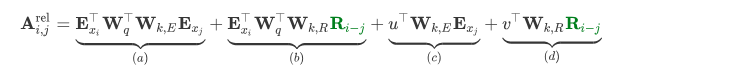
这里是的词embedding,是变换矩阵。a项是 content-based attention,我们已经在上面计算过了。b和d是基于相对位置嵌入的,并且依赖于和之间的距离。u和v是表示对特定内容和特定位置的偏差的全局偏差术语。
下面让我们来看看b到d的具体实现。我们首先加入content bias (c项),因为它是最容易计算的。
1 | u = torch.rand(17).expand_as(q_tfmd) |
接下来,计算所需的相对位置嵌入。对于相对位置嵌入,Transformer-XL使用固定的正弦嵌入。
1 | pos_idxs = torch.arange(seq + prev_seq - 1, -1, -1.0, dtype=torch.float) |
1 | inv_freq = 1 / (10000 ** (torch.arange(0.0, embedding_dim, 2.0) / embedding_dim)) |

1 | pos_idxs = torch.arange(seq + prev_seq - 1, -1, -1.0, dtype=torch.float) |
1 | relative_positional_embeddings.shape |
将上述合在一起为:
1 | class PositionalEmbedding(nn.Module): |
我们还需要对keys/values的位置嵌入纬度进行变换。
1 | linear_p = nn.Linear(embedding_dim, inner_dim) |
因此,将位置偏差添加到attention计算过程中。
1 | v = torch.rand(17) # positional bias |
由于我们需要为每个key-query对计算相对位置嵌入,所以上述中使用相对位置嵌入来实现注意力的简单实现在计算复杂度方面为O(n^2)。幸运的是,原作者提出了一个技巧,通过计算一个query的attention,然后为不同的query位置转移其嵌入,从而将时间减少到O(n)(具体可以见上述公式)。
1 | zero_pad = torch.zeros((seq, 1, batch_size), dtype=torch.float) |
因此,总的attention score为:
1 | raw_attn = content_attn + pos_attn |
当我们进行语言建模时,我们需要阻止模型查看它应该预测的单词。在Transformer中,我们通过将attention score设置为0来实现这一点。这将掩盖了我们不希望模型看到的字。
1 | mask = torch.triu( |
接下来计算value的加权和:
1 | attn = torch.softmax(raw_attn, dim=1) |
最后,将attn_weighted_sum的纬度转换回原来纬度,并使用残差连接层和层标准化,即:
1 | linear_out = nn.Linear(inner_dim, embedding_dim) |
MultiHeadAttention模块
结合上述代码模块,并增加dropout层,我们将得到一个MultiHeadAttention模块。
1 | from typing import * |
我们使用一个随机数进行测试是否正确,如下:
1 | mha = MultiHeadAttention(32, 17, n_heads=4) |
Decoder
在deocder模块中,除了MultiHeadAttention 层外,还需要FFN。
1 | class PositionwiseFF(nn.Module): |
则Decoder模块如下:
1 | class DecoderBlock(nn.Module): |
现在有了上述模块,我们就可以构建完整的Transformer-XL模型了。
除了上面提到的,我们还没有涉及到的语言建模的一个常见技巧是将输入嵌入矩阵E和输出投影矩阵P绑定在一起。请记住,语言模型预测序列中的下一个token,因此它的输出维度是,其中是vocab的大小。如果我们将倒数第二层的输出约束为与嵌入层相同的维度,则嵌入矩阵的shape为,输出投影矩阵的形状为。
将,可以提高性能,同时大大减少模型的总参数(从而减少内存使用量!)
1 | import torch.nn.functional as F |
因此完整的Transformer-XL代码为:
1 | class TransformerXL(nn.Module): |
同样使用一个随机数进行测试,如下:
1 | transformer = TransformerXL(1000, 4, 3, 32, 17, 71, mem_len=5) |
数据加载
Transformer-XL的数据加载类似于基于rnn的语言模型的数据加载,但与标准的数据加载有很大的不同。
假设我们将输入分成4个单词的序列输入到模型中。请记住Transformer-XL是有状态的,这意味着每个mini-batch的计算将被转移到下一个mini-batch。对于mini-batch为1的情况,处理起来很简单。我们只是把输入分成块,然后像这样输入到模型中:

如果批大小是2会发生什么?我们不能像这样拆分句子,否则,我们将打破片段之间的依赖关系。
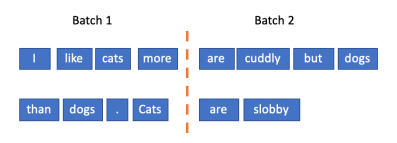
处理batch size为2的语料库的正确方法,应为:
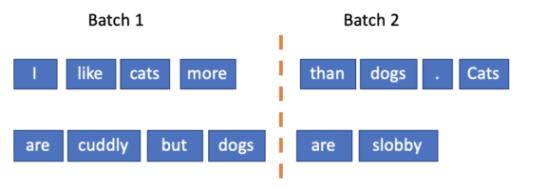
在此基础上,我们首先将语料库划分成batch size的长度片段,然后将每个片段逐块输入到模型中。让我们来看一个例子。假设batch size 为4,我们的整个语料库是这样的:
1 | pytorch is an amazing deep learning framework that makes nlp really easy |
我们想要确保前一batch包含在相同位置上的前一段。换句话说,假设我们一次向模型输入一个单词,我们希望像这样迭代这个句子
1 | Batch 1: pytorch amazing framework nlp |
注意,这意味着你通过从上到下,从左到右,而不是从左到右,从上到下来重新构造原句子。实际上,每个batch中的单词序列的长度通常为bptt(时间反向传播)长度,因为这是梯度沿序列方向传播的最大长度。例如,当bptt长度为2时,batch的shape为(batch_size, bptt):
1 | Batch 1: pytorch amazing framework nlp |
我们可以实现这在一个数据加载这样:
1 | from torch.utils import data |
测试结果如下:
1 |
|
完整代码
下载数据集,新建一个名为download_data.sh脚本文件,并写入以下内容:
1 | !/bin/bash |
运行sh download_data.sh命令进行自动下载数据集。
新建一个名为vocabulary.py文件,并写入以下内容:
1 | from collections import Counter, OrderedDict |
改脚本主要处理语料数据,接下里新建一个名为trainsformer_xl.py文件,并写入以下内容:
1 | import sys |
运行python trainsformer_xl.py命令,将得到以下结果:
1 | {'loss': 6.048809673745043, 'ppl': 423.6084975087664} |
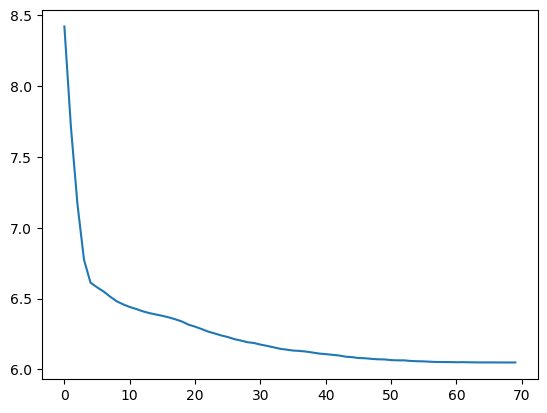
训练loss变化
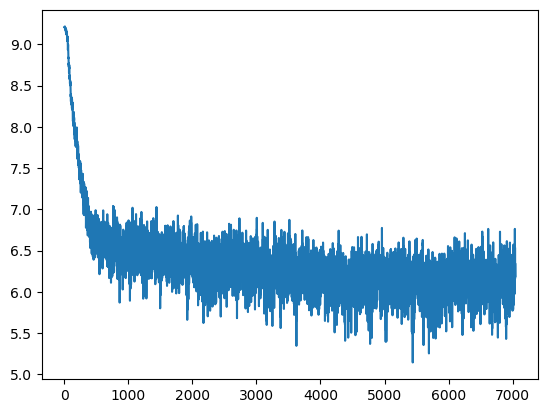
验证loss变化