深度学习与计算机视觉(PB-06)-模型集成

在本章中，我们将探讨集成方法的概念——多个分类器合并成一个大型元分类器的过程。将多个模型的平均结果最为最终结果，可以比随机的单一模型获得更高的性能（比如准确度）。事实上，几乎你所看到的在ImageNet数据挑战赛上获得最佳的结果都是通过集成多个卷积神经网络结果得到的。

首先，我们将讨论下Jensen不等式，这是集成方法的关键。然后，我们相互独立地训练多个CNN模型，并对每个CNN模型进行评估，最后，将多个训练好的cnn模型融合成一个元分类器，并评估元分类器的性能。

集成方法

集成方法通常指的是训练“大量”的模型(其中‘量’的确切值取决于分类任务)，然后通过投票或平均方法将多个模型的输出结果合并成一个结果，以提高分类的准确性。事实上，集成方法并不是专门针对深度学习和卷积神经网络的。一直以来我们使用了很多集成方法，比如AdaBoost[18]和Random forest[19]等技术都是集成方法的典型例子。

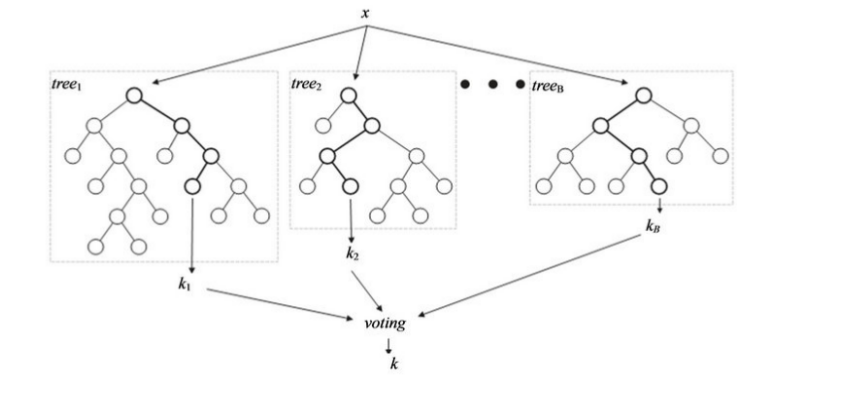
比如在随机森林中，我们独立地训练多棵决策树[20,21]，并由这些决策树组成一个大森林，最后利用组合得到的森林进行预测。如图6.1所示，随机森林由多棵决策树组成，每棵决策树都会返回一个自身的预测结果。这些结果将组成一个元分类器结果表，通过投票方法从结果表中返回出现最多的标签作为最后的预测结果。

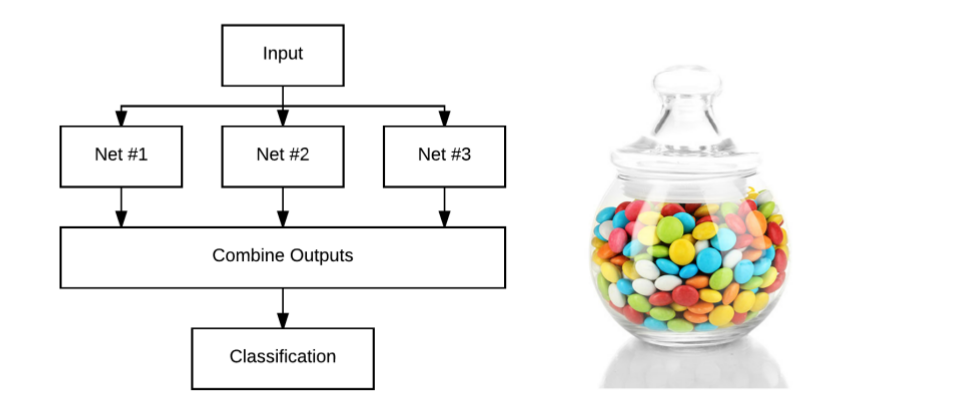
图6.1 随机森林模型结构图同样的概念也适用于深度学习和卷积神经网络。我们可以训练多个网络，且每个网络都会返回每一个标签的概率(如图6.2左)。然后，计算多个概率值的平均值，该平均值就是最后的预测结果。

为什么对多个模型进行平均预测是有效的？我们首先了解下Jensen不等式，然后通过实践表明集成方法的有效性。

图6.2 左：集成网络结构，右：糖果罐 ### Jensen 不等式

一般来说，集成方法是通过融合一个有限的模型集合的结果获得比集合中单模型更好的准确度的过程。Dietterich[23]的开创性研究详细阐述了为什么集成方法通常比单个模型会获得更高的准确度。

Dietterich研究的成功主要取决于Jensen不等式，即机器学习文献中的“多样性”或“奇异值分解”。Jensen不等式的定义表明，凸函数(average)集成的误差小于或等于各模型的平均误差，当然这可能是由于其中一个单模型的误差低于所有模型的平均误差，但是，总的来说，可以确信的是平均所有模型的结果不比随机单模型差。

通过一个简单例子来解释Jensen不等式和模型平均的概念，比如图6.2右，让你猜猜罐子里面有多少糖果。

能猜出有多少糖果吗?100个?200个?500个？在没有参考的情况下，只能凭借自己的感觉。

但是，这个游戏有一个小技巧——基于Jensen不等式。如果你问我罐子里有多少糖果，我就会去问你和每个购买了书籍的人，问他们每个人认为糖果的数量是多少。然后我把所有的猜测都加起来，取平均值作为我的最终预测。

也许，其中有几个人的结果很接近真实的数量，也有几个人的结果偏离真实的数量，但是，在未知的情况下，我们无法根据任何的准则来评估哪个人的结果较接近真实的数量。所以我取每个人的结果平均值，至少平均而言，我的结果不比你随机选择一个结果差。本质上，这就是Jensen不等式。

随机猜测糖果数量游戏和深度学习模型的区别在于，假设CNNs训练很好[具有一定的准确度]，这时预测结果就有一定的可靠性，而不是随机猜测。因此，取多个cnn模型结果的平均值，往往分类准确度会得到一定的提高。所以在深度学习一些公开比赛中，排名靠前的结果基本都是训练了多种模型，然后对多个模型进行集成得到最后的结果，准确率往往会提高。

CNN集成

在构建一个CNNs集成模型之前，我们需要独立训练多个CNN模型。在之前章节中，我们已经看到了许多训练单个CNN的例子——但是我们如何训练多个网络呢?总的来说，我们有两个选择:

1.运行多次训练单个网络的脚本，将每次输出的模型权重进行保存。
2.创建一个单独的Python脚本，该脚本使用for循环来训练N个网络，并在每次迭代结束时输出序列化的模型。

这两种方法都是完全可以接受的。第一种方法比较简单，多次运行命令就可以生成多个cnn模型。下面我们尝试第二个方法，新建一个文件，命名为train_models.py，写入以下代码:

#encoding:utf-8
#设置图像的背景
import matplotlib
matplotlib.use('ggplot')

# 加载模块
from sklearn.preprocessing import LabelBinarizer
from sklearn.metrics import classification_report
from pyimagesearch.nn.conv import MiniVGGNet as MVN
from keras.preprocessing.image import ImageDataGenerator
from keras.optimizers import SGD
from keras.datasets import cifar10
import matplotlib.pyplot as plt
import numpy as np
import argparse
import os

说明：从加载的模块中可以看到

1.主要训练多个MiniVGGNet模型进行融合
2.对CIFAR-10数据进行了数据增强处理
3.使用随机梯度下降法进行优化

定义命令行参数:

# 解析命令行参数
ap = argparse.ArgumentParser()
ap.add_argument('-o','--output',required=True,help='path to output directory')
ap.add_argument('-m','--models',required=True,help='path to output models directory')
ap.add_argument('-n','--num_models',type = int,default=5,help='# of models to train')
args = vars(ap.parse_args())

其中:

–output: 输出结果保存目录。
–models：保存模型权重目录
–num_models: 训练模型个数，默认值为5

一般传统的集成模型都是有多个[几十或者上百]个基础模型组成，比如随机森林由超过30棵决策树组成（大部分情况下都是超过100棵）。而CNNs集成主要由几个卷积神经网络[一般是5-10个]组成，因为训练CNN模型比较耗时且计算昂贵。

在这节实验中，我们主要使用的CIFAR-10数据集进行实验，首先，从磁盘中加载数据到内存中，并对内存中的数据进行预处理，如下代码：

# 加载数据集，并划分为train和test数据
# 图像数据预处理：归一化
((trainX,trainY),(testX,testY)) = cifar10.load_data()
trainX  = trainX.astype('float') / 255.0
testX = testX.astype('float') / 255.0

# 标签进行编码化处理

lb = LabelBinarizer()
trainY = lb.fit_transform(trainY)
testY = lb.fit_transform(testY)

# 初始化标签名陈
labelNames = ["airplane", "automobile", "bird", "cat", "deer",
"dog", "frog", "horse", "ship", "truck"]

进行数据增强处理：

# 初始化数据增强模块
aug = ImageDataGenerator(rotation_range=10,width_shift_range=0.1,
                         height_shift_range=0.1,horizontal_flip=True,
                         fill_mode='nearest')

主要对初始图像进行随机旋转，平移等变换操作，下面，针对数据集单独训练多个MiniVGGNet模型：

# 遍历模型训练个数
for i in np.arange(0,args['num_models']):
    # 初始化优化器和模型
    print("[INFO] training model {}/{}".format(i+1,args['num_models']))
    opt = SGD(lr = 0.01,decay=0.01/ 40,momentum=0.9,
              nesterov=True)
    model = MVN.MiniVGGNet.build(width=32,height=32,depth=3,
                                 classes = 10)
    model.compile(loss = 'categorical_crossentropy',optimizer=opt,metrics = ['accuracy'])

其中，在优化器SGD中，学习率lr= 0.01，动量g = 0.9，并使用Nesterov进行加速——Nesterov是Momentum的变种，与Momentum唯一区别就是，计算梯度的不同，Nesterov先用当前的速度v更新一遍参数，在用更新的临时参数计算梯度，具体的算法可以参考如下图所示：

Nesterov 下面，我们开始训练模型，并将模型权重保存到磁盘中。

# 训练网络
H = model.fit_generator(aug.flow(trainX,trainY,batch_size=64),
                        validation_data=(testX,testY),epochs=40,
                        steps_per_epoch=len(trainX) // 64,verbose = 1)
# 将模型保存到磁盘中
p = [args['models'],"model_{}.model".format(i)]
model.save(os.path.sep.join(p))

在网络完成训练之后，保存模型的评估结果:

# 评估模型
predictions = model.predict(testX,batch_size=64)
report = classification_report(testY.argmax(axis =1),
                               predictions.argmax(axis =1),target_names=labelNames)
# 将模型结果保存到文件中
p = [args['output'],'model_{}.text'.format(i)]
with open(os.path.sep.join(p),'w') as fw:
    fw.write(report)

绘制模型的损失和精度，查看单个模型的性能：

# loss函数可视化
p = [args['output'],'model_{}.png'.format(i)]
plt.style.use('ggplot')
plt.figure()
plt.plot(np.arange(0,40),H.history['loss'],
         label = 'train_loss')
plt.plot(np.arange(0,40),H.history['val_loss'],
         label = 'val_loss')
plt.plot(np.arange(0,40),H.history['acc'],
         label = 'train-acc')
plt.plot(np.arange(0,40),H.history['val_acc'],
         label = 'val-acc')
plt.title("Training Loss and Accuracy for model {}".format(i))
plt.xlabel("Epoch #")
plt.ylabel("Loss/Accuracy")
plt.legend()
plt.savefig(os.path.sep.join(p))
plt.close()

需要注意的是，我们永远不会直接进行集成训练——我们首先要进行一系列实验，以确定模型架构、优化器和超参数的具体信息，保证在给定的数据集中能够产生最高的精度。一旦确定了具体信息之后，我们就可以训练多个模型来形成一个模型集合。所以，直接训练集成方法是不合理的，因为我们还不知道什么样的体系结构、哪种优化器和具体的超参数对给定的数据集最有效。从之前的内容中，我们知道使用SGD训练的MiniVGGNet的准确度约为83%，下面通过应用集成方法，我们希望能够增加准确度。

只需执行以下命令，就可以开始训练模型:

1	$ python train_models.py --output output --models models

训练了5个模型，查看输出路径，如:

1
2
3

$ ls output/
model_0.png model_1.png model_2.png model_3.png model_4.png
model_0.txt model_1.txt model_2.txt model_3.txt model_4.txt

使用grep，我们可以轻松提取每个网络的分类结果:

$ grep ’avg / total’ output/*.txt
output/model_0.txt:avg / total 0.83 0.83 0.82 10000
output/model_1.txt:avg / total 0.83 0.83 0.82 10000
output/model_2.txt:avg / total 0.83 0.83 0.82 10000
output/model_3.txt:avg / total 0.82 0.82 0.81 10000
output/model_4.txt:avg / total 0.83 0.83 0.82 10000

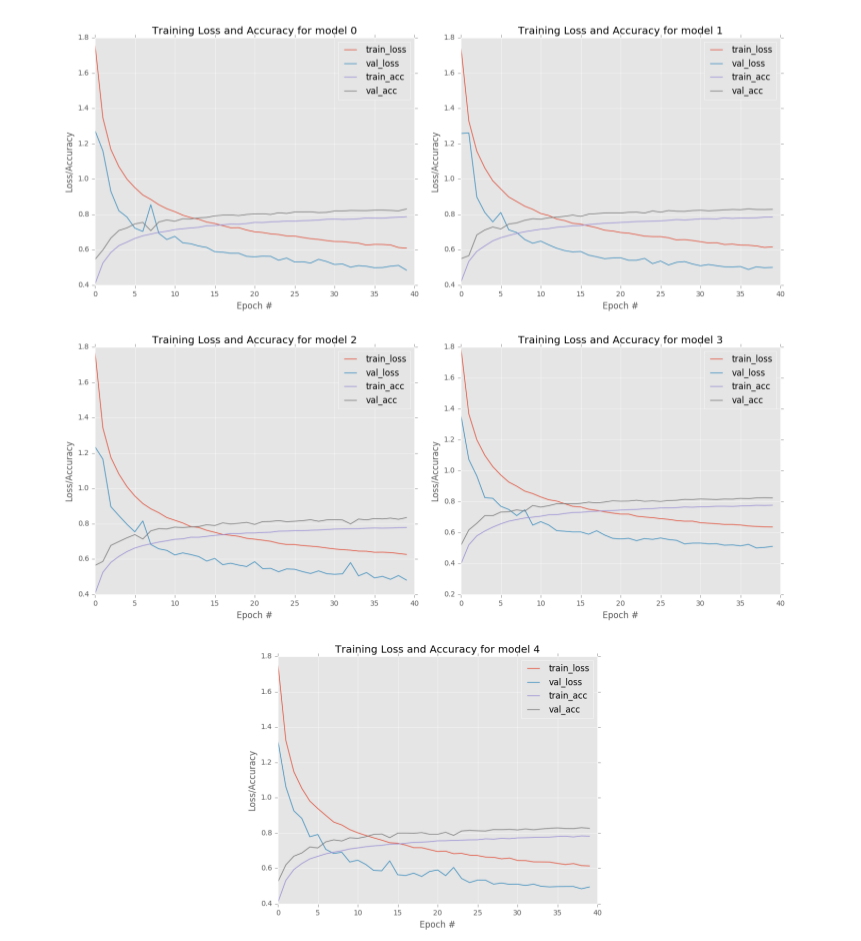
从结果中可以看到，5个模型中有4个获得82%的分类准确率，而其余的模型只有81%的准确率。并从图6.3中可以看到每组学习曲线都有些相似，但是仔细看又有一些不同，这表明每个MiniVGGNet模型以不同的方式进行“学习”。

图6.3 训练结果既然我们已经单独训练了5个模型，下面将它们进行结合进行预测结果，看看分类精度是否有提高。

集成评估

新一个名为test_ensemble.py文件，写入以下代码:

#encoding:utf-8
# 加载所需模块
from sklearn.preprocessing import LabelBinarizer
from sklearn.metrics import classification_report
from keras.models import load_model
from keras.datasets import cifar10
import numpy as np
import argparse
import glob
import os

#命令行参数
ap = argpase.ArgumentParser()
ap.add_argument('-m','--models',required=True,help='path to models directory')
args = vars(ap.parse_args())

其中，命令行参数中:

–models: 模型权重保存路径，这里加载权重时使用

加载CIFAR-10数据集，这里只保留test数据集进行预测:

# 加载数据集，并进行预处理
(testX,testY) = cifar10.load_data()[1]
testX = testX.astype('float') / 255.0
# 初始化标签名称
labelNames = ["airplane", "automobile", "bird", "cat", "deer",
              "dog", "frog", "horse", "ship", "truck"]
# 类别one-hot编码
lb = LabelBinarizer()
testY = lb.fit_transform(testY)

加载训练好的模型权重：

# 遍历模型
modelPaths = os.path.sep.join([args['models'],"*.model"])
modelPaths = list(glob.glob(modelPaths))
models = []

保存的模型路径结构:

1 2	[’models/model_0.model’, ’models/model_1.model’, ’models/model_2.model’, ’models/model_3.model’, ’models/model_4.model’]

从磁盘中加载每一个模型:

1
2
3

for (i,modelPath) in enumerate(modelPaths):
    print("[INFO] loading model {}/{}".format(i+1,len(modelPaths)))
    models.append(load_model(modelPath))

构建一个集成模型结果，并进行评估：

# 初始化
print("[INFO] evaluating ensemble...")
predictions = []
#遍历模型
for model in models:
    # 模型预测
    predictions.append(model.predict(testX,batch_size=64))

# 平均所有模型结果
predictions = np.average(predictions,axis = 0)
# 模型结果
print(classification_report(testY.argmax(axis =1),
                            predictions.argmax(axis=1),target_names=labelNames))

首先，我们会初始化一个预测列表，该列表主要保存每一个模型对test数据的预测结果。CIFAR-10数据集总共有10000张图像，10种类别，因此，每一个模型会产生一个(10000,10)的数组。遍历完5个模型预测之后，我们会得到一个shape为(5,10000,10)的predictions列表。而我们的真实数据shape为(10000,1),因此，我们需要对多个结果进行处理，常见的处理方法为取多个模型的平均值，如第6行代码所示，对得到的5个模型结果进行平均处理，将得到shape为(10000,10)的predictions列表，将predictions列表结果作为最后的输出。

为了确定我们的MiniVGGNet模型集合是否提高了分类精度，执行以下命令:

1	$ python test_ensemble.py --models models

结果如下；

             precision    recall  f1-score   support

   airplane       0.87      0.85      0.86      1000
 automobile       0.91      0.94      0.93      1000
       bird       0.82      0.68      0.75      1000
        cat       0.76      0.55      0.64      1000
       deer       0.78      0.78      0.78      1000
        dog       0.84      0.66      0.74      1000
       frog       0.61      0.97      0.75      1000
      horse       0.87      0.89      0.88      1000
       ship       0.93      0.90      0.92      1000
      truck       0.86      0.93      0.89      1000

avg / total       0.83      0.81      0.81     10000