Gradient Boosting Machine(GBM）调参方法详解

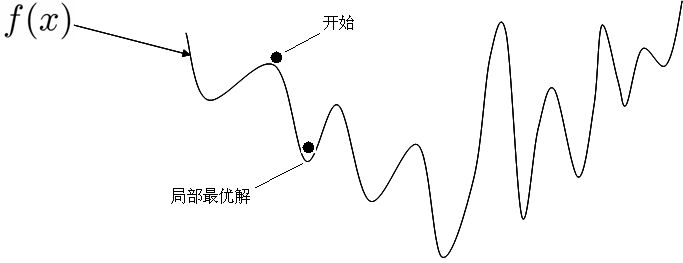
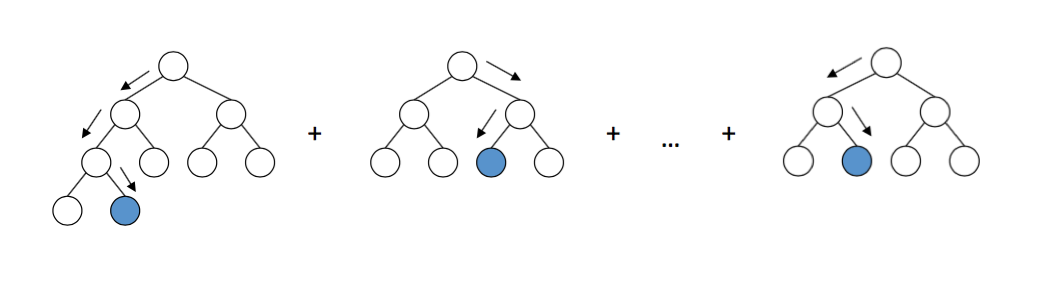
如果一直以来你只把GBM当作黑匣子，只知调用却不明就里，是时候来打开这个黑匣子一探究竟了！

这篇文章是受Owen Zhang (DataRobot的首席产品官，在Kaggle比赛中位列第三)在NYC Data Science Academy里提到的方法启发而成。他当时的演讲大约有2小时，我在这里取其精华，总结一下主要内容。

不像bagging算法只能改善模型高方差（high variance）情况，Boosting算法对同时控制偏差（bias）和方差都有非常好的效果，而且更加高效。如果你需要同时处理模型中的方差和偏差，认真理解这篇文章一定会对你大有帮助，因为我不仅会用Python阐明GBM算法，更重要的是会介绍如何对GBM调参，而恰当的参数往往能令结果大不相同。

特别鸣谢：非常感谢Sudalai Rajkumar对我的大力帮助，他在AV Rank中位列第二。如果没有他的指导就不会有这篇文章了。

1.目录

Boosing是怎么工作的？
理解GBM模型中的参数
学会调参（附详例）

2.Boosting是如何工作的？

Boosting可以将一系列弱学习因子（weak learners）相结合来提升总体模型的预测准确度。在任意时间t，根据t-1时刻得到的结果我们给当前结果赋予一个权重。之前正确预测的结果获得较小权重，错误分类的结果得到较大权重。回归问题的处理方法也是相似的。

让我们用图像帮助理解：

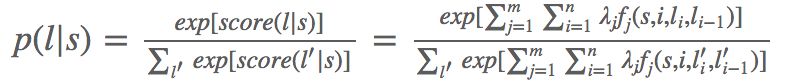
图一：第一个弱学习因子的预测结果（从左至右）
一开始所有的点具有相同的权重（以点的尺寸表示）。
分类线正确地分类了两个正极和五个负极的点。
图二：第二个弱学习因子的预测结果
在图一中被正确预测的点有较小的权重（尺寸较小），而被预测错误的点则有较大的权重。
这时候模型就会更加注重具有大权重的点的预测结果，即上一轮分类错误的点，现在这些点被正确归类了，但其他点中的一些点却归类错误。
对图3的输出结果的理解也是类似的。这个算法一直如此持续进行直到所有的学习模型根据它们的预测结果都被赋予了一个权重，这样我们就得到了一个总体上更为准确的预测模型。

现在你是否对Boosting更感兴趣了？不妨看看下面这些文章（主要讨论GBM）：

3.GBM参数

总的来说GBM的参数可以被归为三类：

1. 树参数：调节模型中每个决定树的性质
2. Boosting参数：调节模型中boosting的操作
3. 其他模型参数：调节模型总体的各项运作

从树参数开始，首先一个决定树的大致结构是这样的：

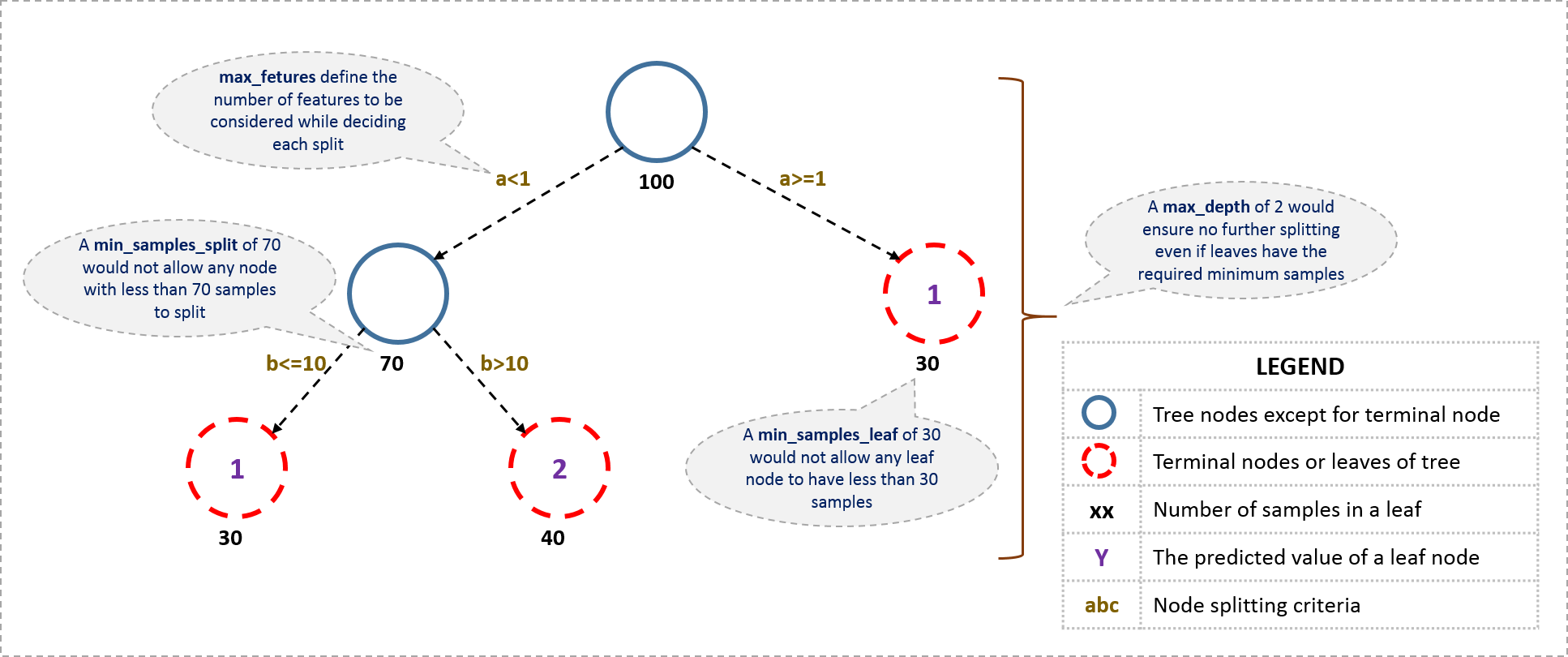
现在我们看一看定义一个决定树所需要的参数。注意我在这里用的都是python里scikit-learn里面的术语，和其他软件比如R里用到的可能不同，但原理都是相同的。

min_ samples_split
定义了树中一个节点所需要用来分裂的最少样本数。
可以避免过度拟合(over-fitting)。如果用于分类的样本数太小，模型可能只适用于用来训练的样本的分类，而用较多的样本数则可以避免这个问题。
但是如果设定的值过大，就可能出现欠拟合现象(under-fitting)。因此我们可以用CV值（离散系数）考量调节效果。
min_ samples_leaf
定义了树中终点节点所需要的最少的样本数。
同样，它也可以用来防止过度拟合。
在不均等分类问题中(imbalanced class problems)，一般这个参数需要被设定为较小的值，因为大部分少数类别（minority class）含有的样本都比较小。
min_ weight_ fraction_leaf
和上面min_ samples_ leaf很像，不同的是这里需要的是一个比例而不是绝对数值：终点节点所需的样本数占总样本数的比值。
2和3只需要定义一个就行了
max_ depth
定义了树的最大深度。
它也可以控制过度拟合，因为分类树越深就越可能过度拟合。
当然也应该用CV值检验。
max_ leaf_ nodes
定义了决定树里最多能有多少个终点节点。
这个属性有可能在上面max_ depth里就被定义了。比如深度为n的二叉树就有最多2^n个终点节点。
如果我们定义了max_ leaf_ nodes，GBM就会忽略前面的max_depth。
max_ features
决定了用于分类的特征数，是人为随机定义的。
根据经验一般选择总特征数的平方根就可以工作得很好了，但还是应该用不同的值尝试，最多可以尝试总特征数的30%-40%.
过多的分类特征可能也会导致过度拟合。

在继续介绍其他参数前，我们先看一个简单的GBM二分类伪代码:

1. 初始分类目标的参数值2. 对所有的分类树进行迭代：
  2.1 根据前一轮分类树的结果更新分类目标的权重值（被错误分类的有更高的权重）
  2.2 用训练的子样本建模
  2.3 用所得模型对所有的样本进行预测
  2.4 再次根据分类结果更新权重值
3. 返回最终结果

以上步骤是一个极度简化的BGM模型，而目前我们所提到的参数会影响2.2这一步，即建模的过程。现在我们来看看影响boosting过程的参数：

learning_ rate
这个参数决定着每一个决定树对于最终结果（步骤2.4）的影响。GBM设定了初始的权重值之后，每一次树分类都会更新这个值，而learning_ rate控制着每次更新的幅度。
一般来说这个值不应该设的比较大，因为较小的learning rate使得模型对不同的树更加稳健，就能更好地综合它们的结果。
n_ estimators
定义了需要使用到的决定树的数量（步骤2）
虽然GBM即使在有较多决定树时仍然能保持稳健，但还是可能发生过度拟合。所以也需要针对learning rate用CV值检验。
subsample
训练每个决定树所用到的子样本占总样本的比例，而对于子样本的选择是随机的。
用稍小于1的值能够使模型更稳健，因为这样减少了方差。
一把来说用~0.8就行了，更好的结果可以用调参获得。

好了，现在我们已经介绍了树参数和boosting参数，此外还有第三类参数，它们能影响到模型的总体功能：

loss
对于分类和回归模型可以有不同的值。一般来说不用更改，用默认值就可以了，除非你对它及它对模型的影响很清楚。
init
它影响了输出参数的起始化过程
如果我们有一个模型，它的输出结果会用来作为GBM模型的起始估计，这个时候就可以用init
random_ state
作为每次产生随机数的随机种子
使用随机种子对于调参过程是很重要的，因为如果我们每次都用不同的随机种子，即使参数值没变每次出来的结果也会不同，这样不利于比较不同模型的结果。
任一个随即样本都有可能导致过度拟合，可以用不同的随机样本建模来减少过度拟合的可能，但这样计算上也会昂贵很多，因而我们很少这样用
verbose
决定建模完成后对输出的打印方式：
0：不输出任何结果（默认）
1：打印特定区域的树的输出结果

1：打印所有结果
warm_ start
这个参数的效果很有趣，有效地使用它可以省很多事
使用它我们就可以用一个建好的模型来训练额外的决定树，能节省大量的时间，对于高阶应用我们应该多多探索这个选项。
presort
决定是否对数据进行预排序，可以使得树分裂地更快。
默认情况下是自动选择的，当然你可以对其更改

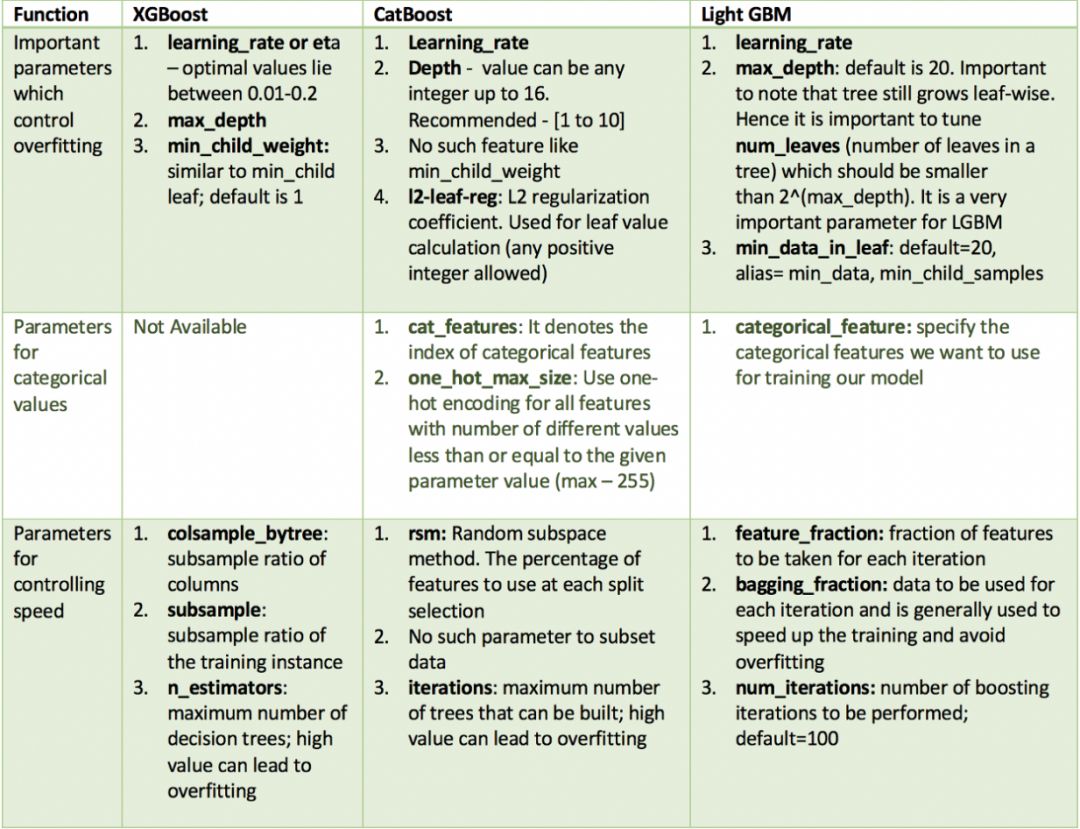
我知道我列了太多的参数，详细可以看下表

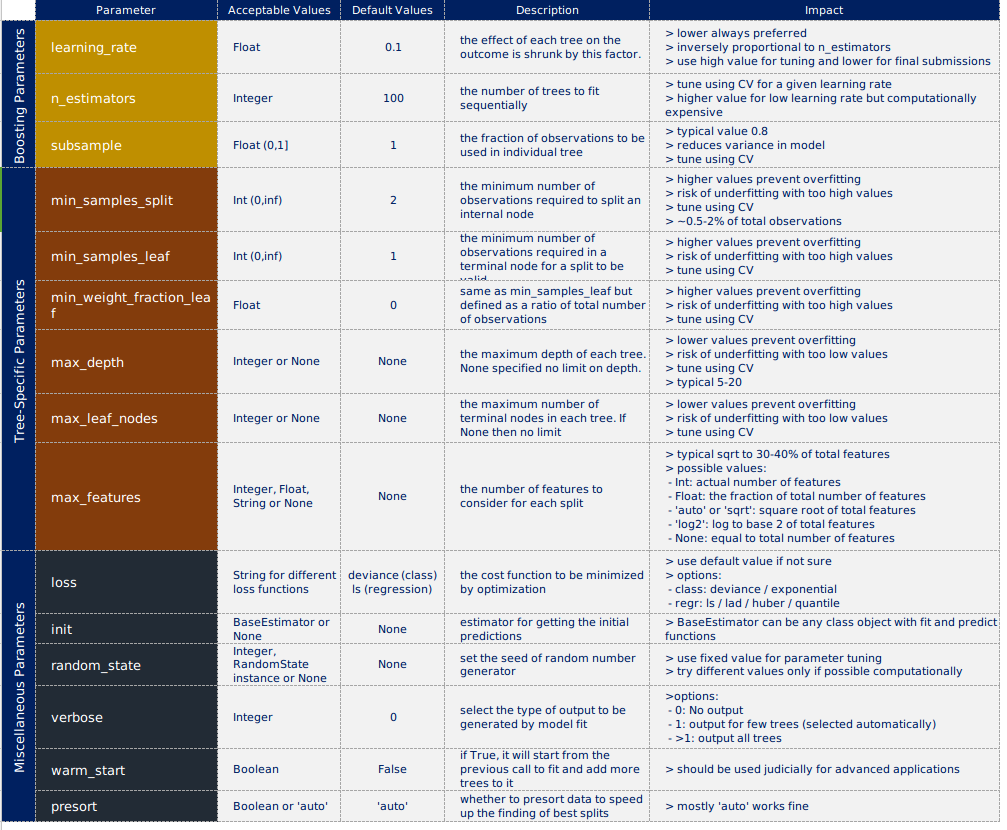
4.参数调节实例

接下来要用的数据集来自Data Hackathon 3.x AV hackathon。比赛的细节可以在比赛网站上找到地址，数据可以从这里下载：地址。我对数据做了一些清洗：

City这个变量已经被我舍弃了，因为有太多种类了。
DOB转为Age|DOB,舍弃了DOB
创建了EMI_Loan_Submitted_Missing这个变量，当EMI_Loan_Submitted 变量值缺失时它的值为1，否则为0。然后舍弃了EMI_Loan_Submitted。
EmployerName的值也太多了，我把它也舍弃了
Existing_EMI的缺失值被填补为0（中位数），因为只有111个缺失值
创建了Interest_Rate_Missing变量，类似于#3，当Interest_Rate有值时它的值为0，反之为1，原来的Interest_Rate变量被舍弃了
Lead_Creation_Date也被舍弃了，因为对结果看起来没什么影响
用Loan_Amount_Applied和 Loan_Tenure_Applied的中位数填补了缺失值
创建了Loan_Amount_Submitted_Missing变量，当Loan_Amount_Submitted有缺失值时为1，反之为0，原本的Loan_Amount_Submitted变量被舍弃
创建了Loan_Tenure_Submitted_Missing变量，当Loan_Tenure_Submitted有缺失值时为1，反之为0，原本的Loan_Tenure_Submitted变量被舍弃
舍弃了LoggedIn,和Salary_Account
创建了Processing_Fee_Missing变量，当Processing_Fee有缺失值时为1，反之为0，原本的Processing_Fee变量被舍弃
Source-top保留了2个，其他组合成了不同的类别
对一些变量采取了数值化和独热编码（One-Hot-Coding）操作

你们可以从GitHub里data_preparation iPython notebook中看到这些改变。

首先，我们加载需要的library和数据：

#encoding:utf-8
import sys
import pandas as pd
import numpy as np
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.grid_search import  GridSearchCV
from sklearn import cross_validation,metrics
import matplotlib.pylab as plt
reload(sys)
sys.setdefaultencoding('utf8')
train = pd.read_csv("train_modified.csv")
target = 'Disbursed'
IDcol = "ID"

然后我们来写一个创建GBM模型和CV值的函数。

def modelfit(alg,dtrain,predictors,performCV = True,printFeatureImportance=True,cv_folds = 5):
    alg.fit(dtrain[predictors],dtrain['Disbursed'])
    dtrain_predictions = alg.predict(dtrain[predictors])
    dtrain_predprob = alg.predict_proba(dtrain[predictors])[:,1]
    if performCV:
        cv_score = cross_validation.cross_val_score(alg,dtrain[predictors],dtrain['Disbursed'],cv=cv_folds,scoring="roc_auc")
    print "\nModel Report:"
    print "Accuracy:%.4g"%metrics.accuracy_score(dtrain['Disbursed'].values,dtrain_predictions)
    print "AUC Score (Train): %f"%metrics.roc_auc_score(dtrain['Disbursed'],dtrain_predprob)
    if performCV:
        print "CV Score:Mean -%.7g | std -%.7g | Min -%.7g | Max -%.7g"%(np.mean(cv_score),np.std(cv_score),np.min(cv_score),np.max(cv_score))
    if printFeatureImportance:
        feat_imp = pd.Series(alg.feature_importances_,predictors).sort_values(ascending=False)
        feat_imp.plot(kind = 'bar',title = "Feature Importances")
        plt.ylabel('Feature Importance Score')
        plt.show()
predictors = [x for x in train.columns if x not in [target,IDcol]]
gbm0 = GradientBoostingClassifier(random_state=10)
modelfit(gbm0,train,predictors)

接着就要创建一个基线模型（baseline model）。这里我们用AUC来作为衡量标准，所以用常数的话AUC就是0.5。一般来说用默认参数设置的GBM模型就是一个很好的基线模型，我们来看看这个模型的输出和特征重要性：

1
2
3

predictors = [x for x in train.columns if x not in [target,IDcol]]
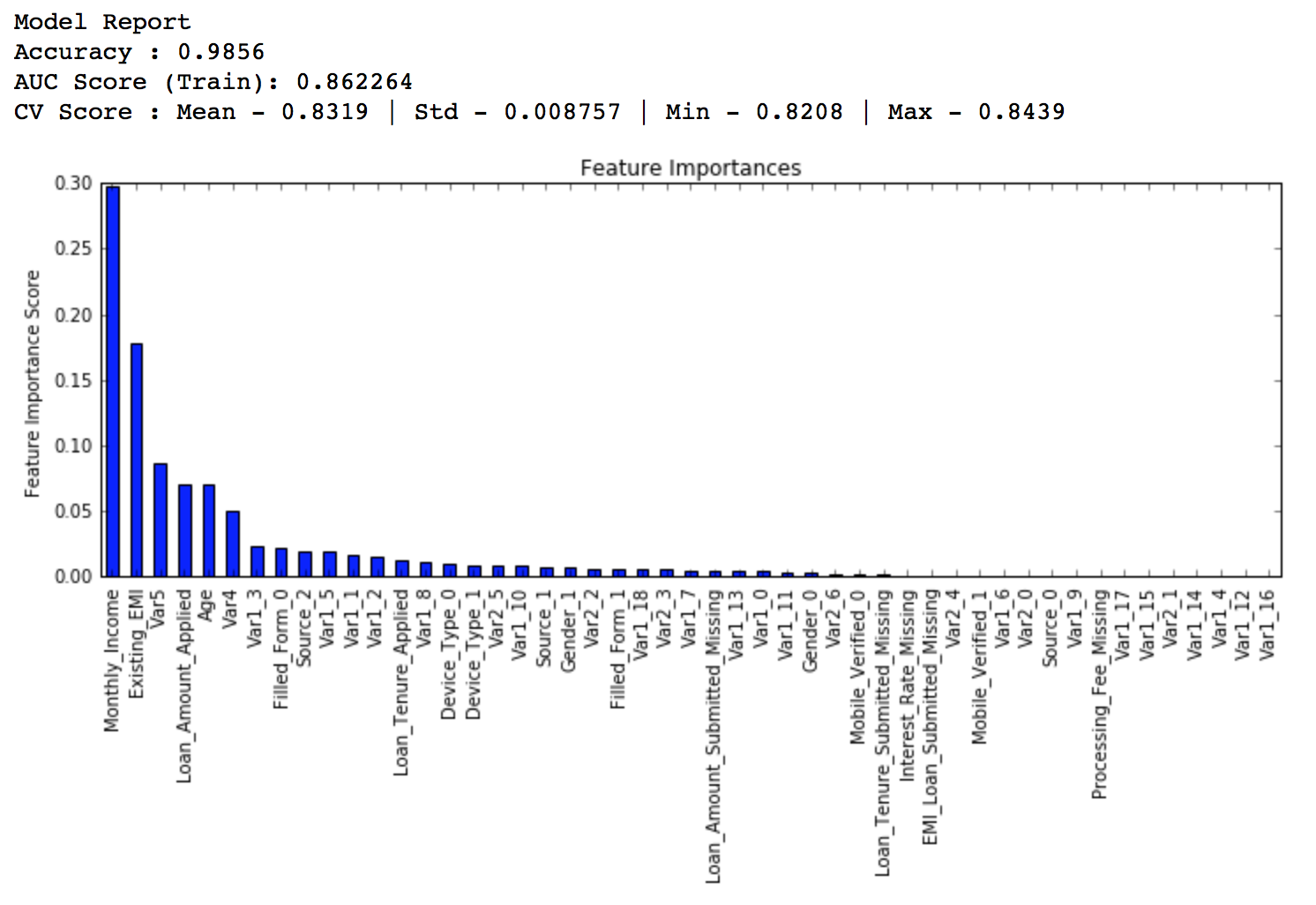
gbm0 = GradientBoostingClassifier(random_state=10)
modelfit(gbm0,train,predictors)

从图上看出，CV的平均值是0.8319，后面调整的模型会做得比这个更好。

4.1 参数调节的一般方法

之前说过，我们要调节的参数有两种：树参数和boosting参数。learning rate没有什么特别的调节方法，因为只要我们训练的树足够多learning rate总是小值来得好。

虽然随着决定树的增多GBM并不会明显得过度拟合，高learing rate还是会导致这个问题，但如果我们一味地减小learning rate、增多树,计算就会非常昂贵而且需要运行很长时间。了解了这些问题，我们决定采取以下方法调参：

选择一个相对来说稍微高一点的learning rate。一般默认的值是0.1，不过针对不同的问题，0.05到0.2之间都可以
决定当前learning rate下最优的决定树数量。它的值应该在40-70之间。记得选择一个你的电脑还能快速运行的值，因为之后这些树会用来做很多测试和调参。
接着调节树参数来调整learning rate和树的数量。我们可以选择不同的参数来定义一个决定树，后面会有这方面的例子
降低learning rate，同时会增加相应的决定树数量使得模型更加稳健

4.2固定 learning rate和需要估测的决定树数量

为了决定boosting参数，我们得先设定一些参数的初始值，可以像下面这样：

min_ samples_ split=500: 这个值应该在总样本数的0.5-1%之间，由于我们研究的是不均等分类问题，我们可以取这个区间里一个比较小的数，500。
min_ samples_ leaf=50: 可以凭感觉选一个合适的数，只要不会造成过度拟合。同样因为不均等分类的原因，这里我们选择一个比较小的值。
max_ depth=8: 根据观察数和自变量数，这个值应该在5-8之间。这里我们的数据有87000行，49列，所以我们先选深度为8。
max_ features=’sqrt’: 经验上一般都选择平方根。
subsample=0.8: 开始的时候一般就用0.8

注意我们目前定的都是初始值，最终这些参数的值应该是多少还要靠调参决定。现在我们可以根据learning rate的默认值0.1来找到所需要的最佳的决定树数量，可以利用网格搜索（grid search）实现，以10个数递增，从20测到80。

#第一步
param_test1 = {
    "n_estimators":range(20,81,10)
}
gsearch1 = GridSearchCV(estimator=GradientBoostingClassifier(
    learning_rate=0.1,
    min_samples_split=500,
    min_samples_leaf=50,
    max_depth=8,
    max_features='sqrt',
    subsample=0.8,
    random_state=10
    ),
    param_grid=param_test1,scoring="roc_auc",n_jobs=4,iid=False,cv=5
)
gsearch1.fit(train[predictors],train[target])
print gsearch1.grid_scores_
print gsearch1.best_params_
print gsearch1.best_score_

来看一下输出结果：

可以看出对于0.1的learning rate, 60个树是最佳的，而且60也是一个合理的决定树数量，所以我们就直接用60。但在一些情况下上面这段代码给出的结果可能不是我们想要的，比如：

如果给出的输出是20，可能就要降低我们的learning rate到0.05，然后再搜索一遍。
如果输出值太高，比如100，因为调节其他参数需要很长时间，这时候可以把learniing rate稍微调高一点。

4.3 调节树参数

树参数可以按照这些步骤调节：

调节max_depth和 num_samples_split
调节min_samples_leaf
调节max_features

需要注意一下调参顺序，对结果影响最大的参数应该优先调节，就像max_depth和num_samples_split。

重要提示：接着我会做比较久的网格搜索(grid search)，可能会花上15-30分钟。你在自己尝试的时候应该根据电脑情况适当调整需要测试的值。

max_depth可以相隔两个数从5测到15，而min_samples_split可以按相隔200从200测到1000。这些完全凭经验和直觉，如果先测更大的范围再用迭代去缩小范围也是可行的。

# 第二步
param_test2 = {
    "max_depth":range(5,16,2),
    "min_samples_split":range(200,1001,200)
}
gsearch2 = GridSearchCV(estimator=GradientBoostingClassifier(
    learning_rate=0.1,
    n_estimators=60,
    max_features='sqrt',
    subsample=0.8,
    random_state=10
    ),
    param_grid=param_test2,scoring="roc_auc",n_jobs=4,iid=False,cv=5
)
gsearch2.fit(train[predictors],train[target])
print gsearch2.grid_scores_
print gsearch2.best_params_
print gsearch2.best_score_

从结果可以看出，我们从30种组合中找出最佳的max_depth是9，而最佳的min_smaples_split是1000。1000是我们设定的范围里的最大值，有可能真正的最佳值比1000还要大，所以我们还要继续增加min_smaples_split。树深就用9。接着就来调节min_samples_leaf，可以测30，40，50，60，70这五个值，同时我们也试着调大min_samples_leaf的值。

#第三步
param_test3 = {
    "min_samples_leaf":range(30,71,10),
    "min_samples_split":range(1000,2100,200)
}
gsearch3 = GridSearchCV(estimator=GradientBoostingClassifier(
    learning_rate=0.1,
    n_estimators=60,
    max_features='sqrt',
    subsample=0.8,
    random_state=10,
    max_depth=9
    ),
    param_grid=param_test3,scoring="roc_auc",n_jobs=4,iid=False,cv=5
)
gsearch3.fit(train[predictors],train[target])
print gsearch3.grid_scores_
print gsearch3.best_params_
print gsearch3.best_score_

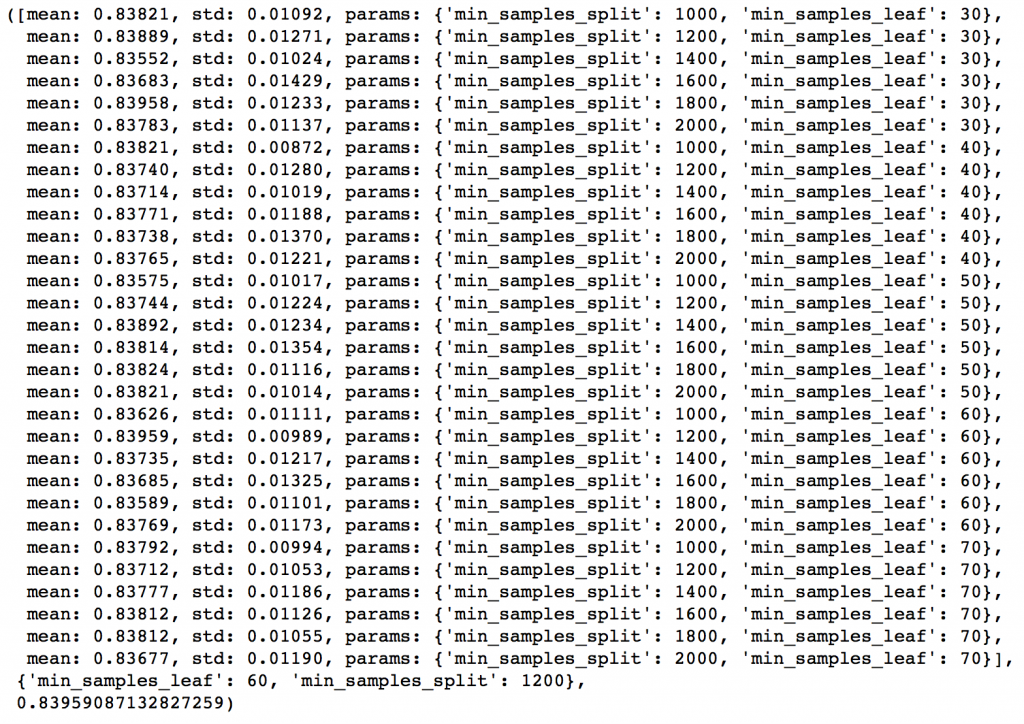
这样min_samples_split的最佳值是1200，而min_samples_leaf的最佳值是60。注意现在CV值增加到了0.8396。现在我们就根据这个结果来重新建模，并再次评估特征的重要性。

1	modelfit(gsearch3.best_estimator_, train, predictors)

比较之前的基线模型结果可以看出，现在我们的模型用了更多的特征，并且基线模型里少数特征的重要性评估值过高，分布偏斜明显，现在分布得更加均匀了。

接下来就剩下最后的树参数max_features了，可以每隔两个数从7测到19。

param_test4 = {
    'max_features':range(7,20,2)
}
gsearch4 = GridSearchCV(estimator = GradientBoostingClassifier(
    learning_rate=0.1,
    n_estimators=60,
    max_depth=9,
    min_samples_split=1200,
    min_samples_leaf=60,
    subsample=0.8,
    random_state=10
    ),
    param_grid = param_test4, scoring='roc_auc',n_jobs=4,iid=False, cv=5
)
gsearch4.fit(train[predictors],train[target])
print gsearch4.grid_scores_, gsearch4.best_params_, gsearch4.best_score_

最佳的结果是7，正好就是我们设定的初始值（平方根）。当然你可能还想测测小于7的值，我也鼓励你这么做。而按照我们的设定，现在的树参数是这样的：

min_samples_split: 1200

min_samples_leaf: 60

max_depth: 9

max_features: 7

4.4 调节子样本比例来降低learning rate

接下来就可以调节子样本占总样本的比例，我准备尝试这些值：0.6,0.7,0.75,0.8,0.85,0.9。

param_test5 = {
    'subsample':[0.6,0.7,0.75,0.8,0.85,0.9]
}
gsearch5 = GridSearchCV(estimator = GradientBoostingClassifier(
    learning_rate=0.1,
    n_estimators=60,
    max_depth=9,
    min_samples_split=1200,
    min_samples_leaf=60,
    subsample=0.8,
    random_state=10,
    max_features=7
    ),
    param_grid = param_test5, scoring='roc_auc',n_jobs=4,iid=False, cv=5
)
gsearch5.fit(train[predictors],train[target])
print gsearch5.grid_scores_, gsearch5.best_params_, gsearch5.best_score_

给出的结果是0.85。这样所有的参数都设定好了，现在我们要做的就是进一步减少learning rate，就相应地增加了树的数量。需要注意的是树的个数是被动改变的，可能不是最佳的，但也很合适。随着树个数的增加，找到最佳值和CV的计算量也会加大，为了看出模型执行效率，我还提供了我每个模型在比赛的排行分数（leaderboard score），怎么得到这个数据不是公开的，你很难重现这个数字，它只是为了更好地帮助我们理解模型表现。

现在我们先把learning rate降一半，至0.05，这样树的个数就相应地加倍到120。

gbm_tuned_1 = GradientBoostingClassifier(
    learning_rate=0.05,
    n_estimators=120,
    max_depth=9,
    min_samples_split=1200,
    min_samples_leaf=60,
    subsample=0.85,
    random_state=10,
    max_features=7,
    warm_start=True
)
modelfit(gbm_tuned_1, train, predictors,performCV=False)

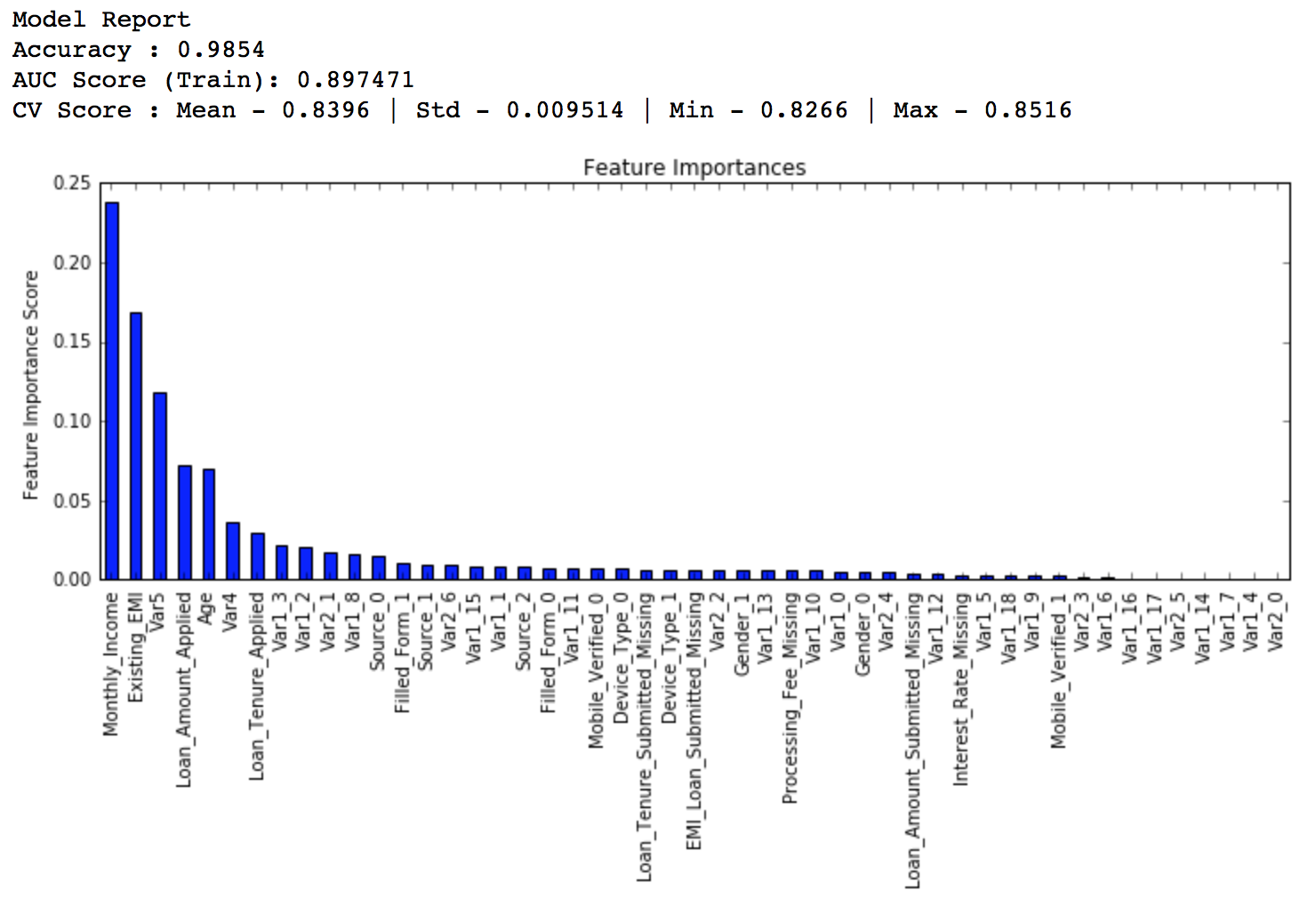
排行得分：0.844139

接下来我们把learning rate进一步减小到原值的十分之一,即0.01，相应地，树的个数变为600。

gbm_tuned_2 = GradientBoostingClassifier(
    learning_rate=0.01,
    n_estimators=600,
    max_depth=9,
    min_samples_split=1200,
    min_samples_leaf=60,
    subsample=0.85,
    random_state=10,
    max_features=7,
    warm_start=True
)
modelfit(gbm_tuned_2, train, predictors,performCV=False)

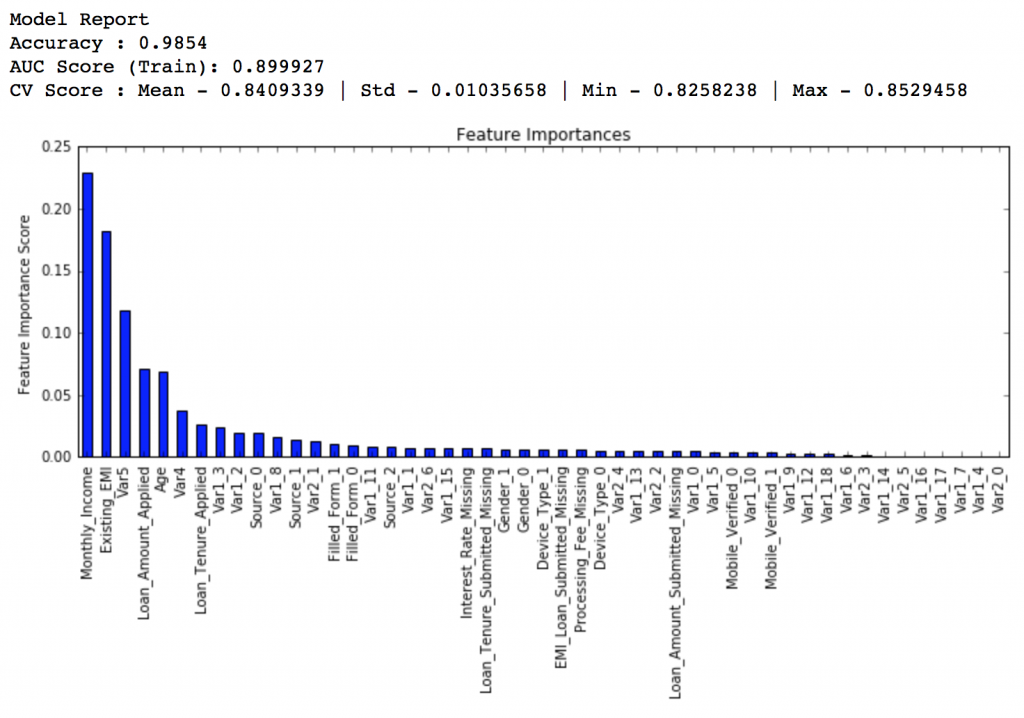
排行得分：0.848145

继续把learning rate缩小至二十分之一，即0.005,这时候我们有1200个树。

gbm_tuned_4 = GradientBoostingClassifier(
    learning_rate=0.005,
    n_estimators=1200,
    max_depth=9,
    min_samples_split=1200,
    min_samples_leaf=60,
    subsample=0.85,
    random_state=10,
    max_features=7,
    warm_start=True
)
modelfit(gbm_tuned_4, train, predictors, performCV=False)

排行得分：0.848112

排行得分稍微降低了，我们停止减少learning rate，只单方面增加树的个数，试试1500个树。

gbm_tuned_4 = GradientBoostingClassifier(
    learning_rate=0.005,
    n_estimators=1500,
    max_depth=9,
    min_samples_split=1200,
    min_samples_leaf=60,
    subsample=0.85,
    random_state=10,
    max_features=7,
    warm_start=True
)
modelfit(gbm_tuned_4, train, predictors, performCV=False)

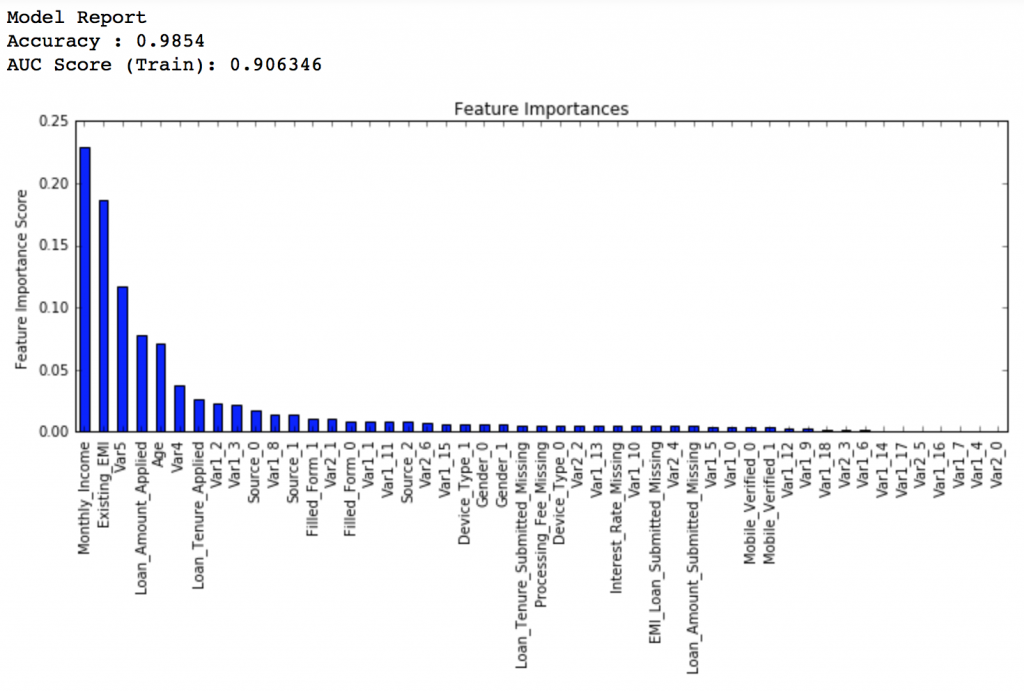
排行得分：0.848747

看，就这么简单，排行得分已经从0.844升高到0.849了，这可是一个很大的提升。

还有一个技巧就是用“warm_start”选项。这样每次用不同个数的树都不用重新开始。所有的代码都可以从我的Github里下载到。

5 总结

这篇文章详细地介绍了GBM模型。我们首先了解了何为boosting，然后详细介绍了各种参数。这些参数可以被分为3类：树参数，boosting参数，和其他影响模型的参数。最后我们提到了用GBM解决问题的一般方法，并且用AV Data Hackathon 3.x problem数据运用了这些方法。最后，希望这篇文章确实帮助你更好地理解了GBM，在下次运用GBM解决问题的时候也更有信心。

原文地址: Complete Guide to Parameter Tuning in Gradient Boosting (GBM) in Python by Aarshay Jain

github地址: https://github.com/aarshayj/Analytics_Vidhya/tree/master/Articles/Parameter_Tuning_GBM_with_Example