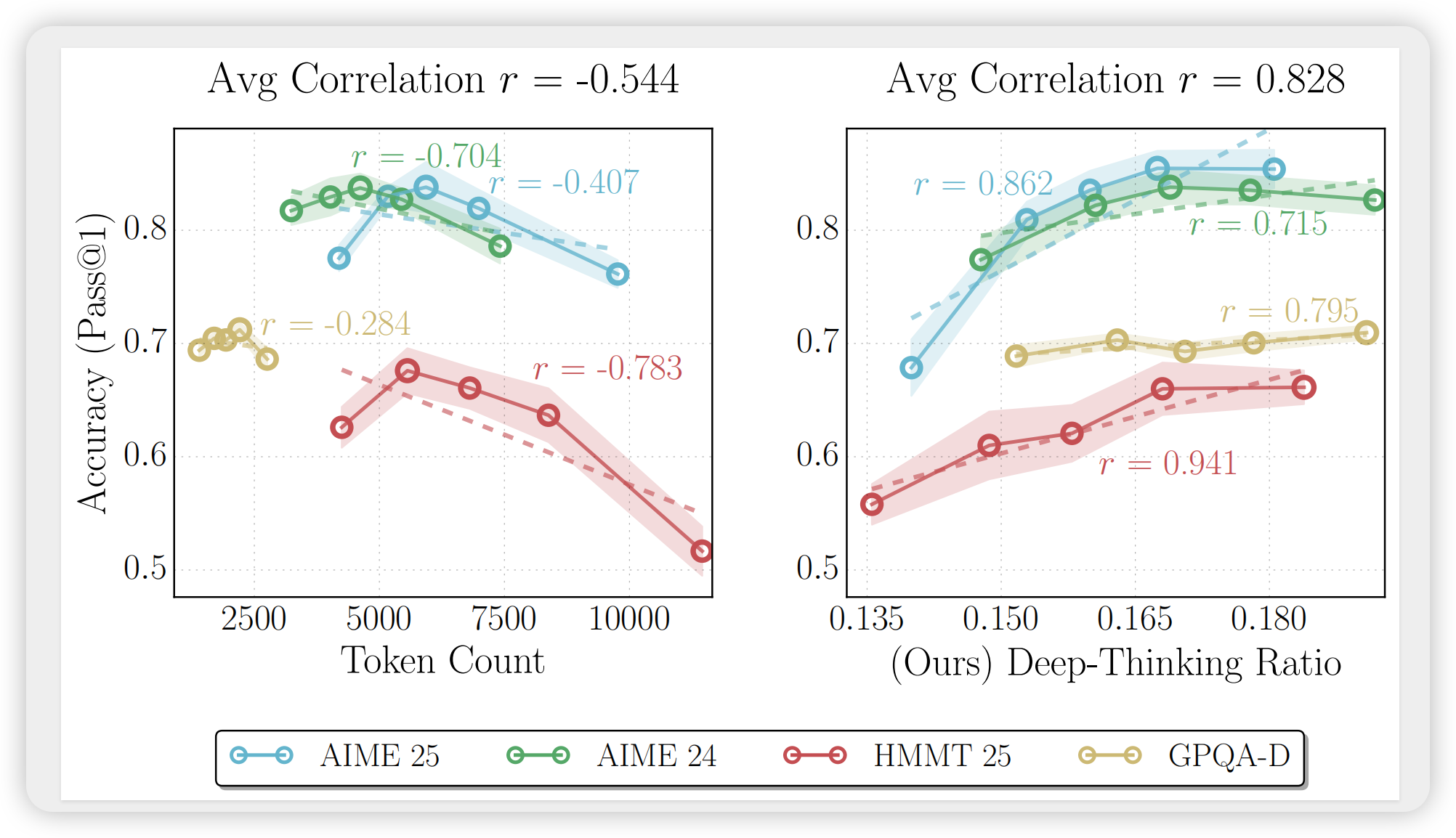
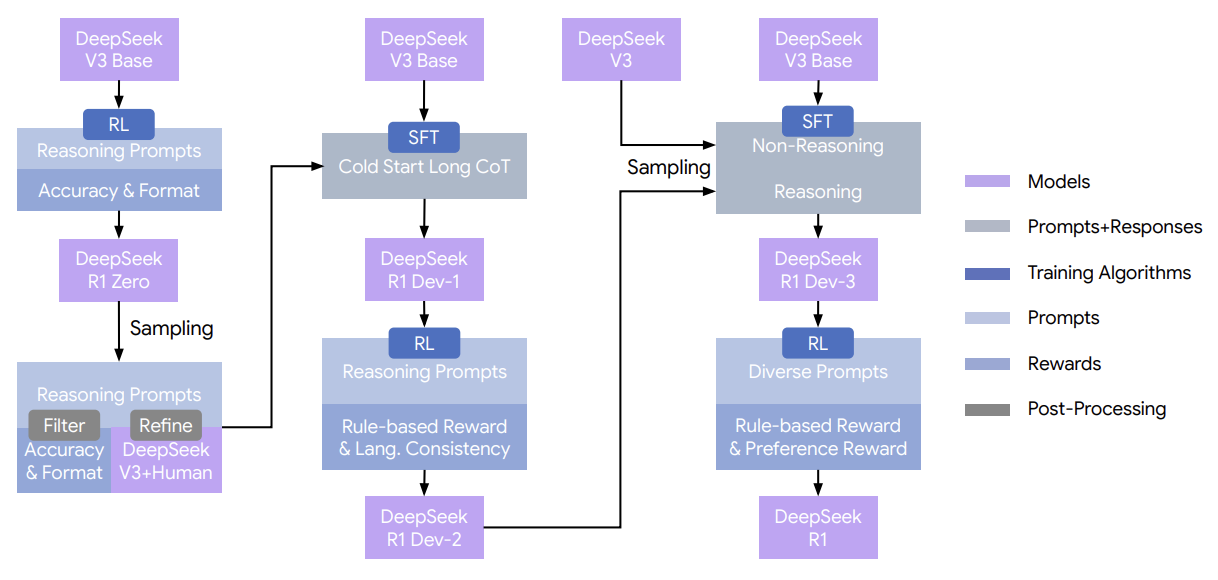
文章在CoNLL03 NER的F1值超过BERT达到了93.09左右，名副其实的state-of-art。考虑到BERT训练的数据量和参数量都极大，而该文方法只用一个GPU训了一周，就达到了state-of-art效果，值得花时间看看，总的来说，作者基于词的上下文字符级语言模型得到该词的表示，该模型的主要好处有:

  • 可以在大型无标签数据集下进行训练。
  • 利用上下文字符嵌入，可以更好地处理罕见和拼写错误的单词。
  • 利用上下文字符嵌入，可以得到多义词的不同语境嵌入。

总的来说，使用BiLSTM模型，用动态embedding取代静态embedding，character-level的模型输出word-level的embedding. 每个词的embedding和具体任务中词所在的整句sequence都有关，算是解决了静态embedding在一词多义方面的短板，综合了上下文信息。另外该模型产生的隐藏状态输出可以用于下游任务中，比如NER任务，如下所示；

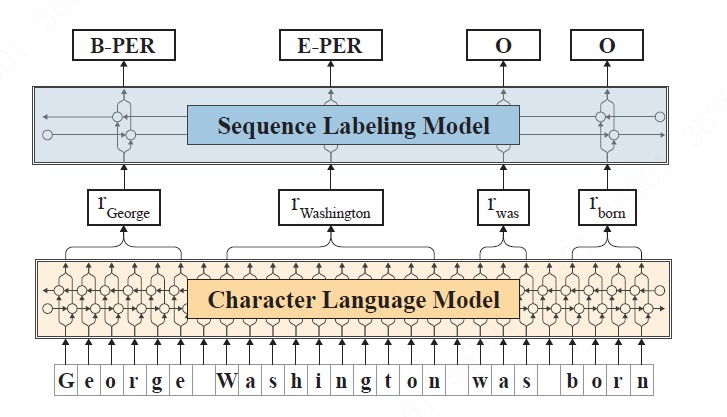
目前三种主流embedding:

  • A. 经典embedding
  • B. character-level 基于特定任务的embedding，不需要预训练，与任务的训练过程同步完成
  • C. 基于上下文的，由深度LSTM各层hidden state的线性组合而成的embedding

本文模型特点：

  • A. 模型以character为原子单位，在网络中，每个character都有一个对应的hidden state. – 这个特点对需要多一步分词的中文来说可能有避免分词错误导致下游function继续错误的弊端。
  • B. 输出以word为单位的embedding, 这个embbeding由前向LSTM中，该词最后一个字母的hidden state 和反向LSTM中该词第一个字母的hidden state拼接组成，这样就能够兼顾上下文信息。具体说明见下图：

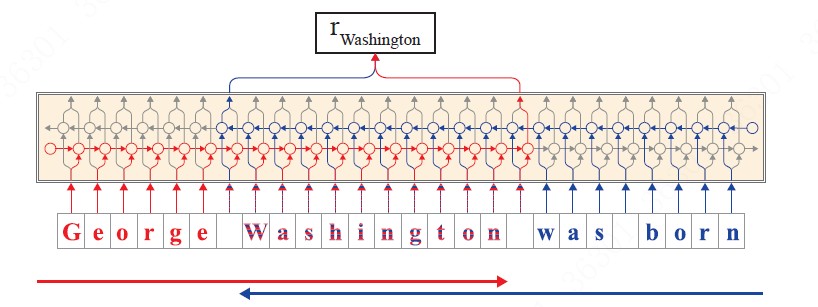
  • 在前向语言模型（红色标记），我们提取单词中最后一个字符后的输出隐藏状态作为该单词的前向表示，因为该隐藏状态包含了从句子的开头到此时传播的信息。
  • 在后向语言模型（蓝色标记），我们在单词中的第一个字符之前提取输出隐藏状态作为该词的后向表示，因为，它包含了从句子末到此时传播的信息。
  • 将两个隐藏状态输出拼接在一起作为该词的最终嵌入。

实验结果

整个实验结果如下表格所示:

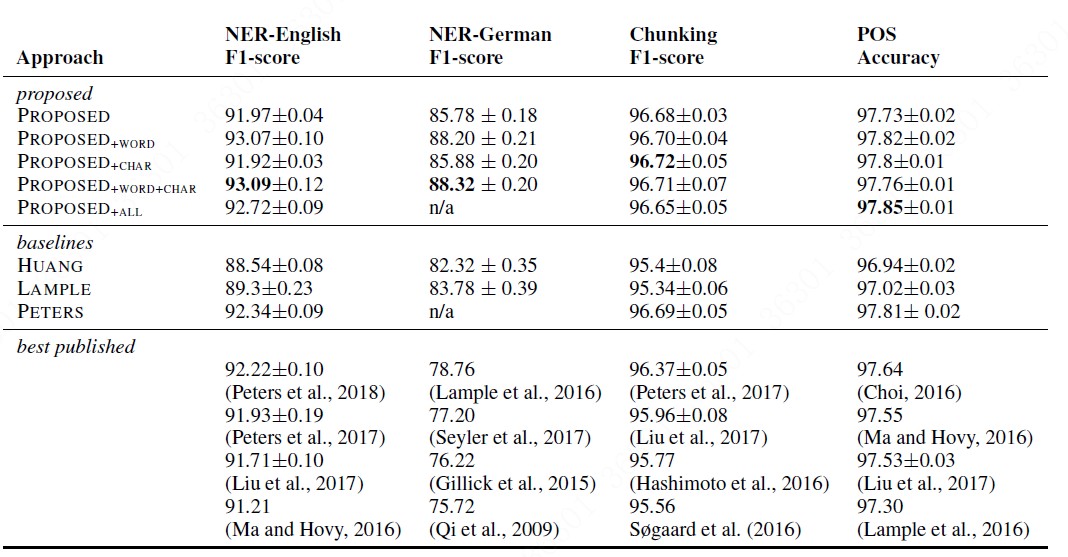
表格中PROPOSED表示文中提出的embedding, word代表经典预训练embedding, char表示任务相关的embedding，可以看出本文的动态embedding + 经典预训练embedding的组合最有效，char-embedding加不加基本没有影响。

模型训练相关参数：

  • 语料库：英文 - 10亿词语料库 德文-5亿词语料库
  • 训练过程： 1个GPU跑了一周

时间性能：

  • 10个单词左右句子产生embedding需要10ms左右，20个单词句子基本就涨到20ms，对生产环境来说勉强可以接受。

备注

原始论文地址: paper

作者公开的Flair框架地址: github

个人参考原作者提供的框架Flair，实现了将中文词转化为笔画模型进行训练的代码。完整中文笔画版本的代码地址: github

** cross entropy与 ppl的关系**

假设xx是一个离散变量，u(x)u(x)和v(x)v(x)是两个与xx相关的概率分布，那么uu和vv之间cross entropy 的定义是在分布uu下−log(v(x))-log(v(x))的期望值：

H(u,v)=Eu[−log⁡v(x)]=−∑xu(x)log⁡v(x)H(u,v) = E_u[-\log v(x)] = - \sum_{x} u(x) \log v(x)

把xx看做单词，u(x)u(x)为每个位置上单词的真实分布，v(x)v(x)为模型的预测分布P(wi∣w1,…,wi−1)P(w_i \mid w_1, \dots ,w_{i-1})，就可以看出 log ppl和cross entropy是等价的。唯一的区别是，由于语言模型的真实分布是未知的，因此在ppl中，真实分布用测试语料中的取样代替。即认为在给定上文w1,w2,…,wi−1w_1,w_2,\dots ,w_{i-1}的条件下，语料中出现单词wiw_i的概率为1，出现其他单词的概率均为0。

u(x∣w1,…,wi−1)={1,x=wi0,x≠wiu(x \mid w_1,\dots,w_{i-1}) = \begin{cases} 1, & x = w_i \\ 0, & x \neq w_i \end{cases}

从而可得到:

H(u,v)=−∑xu(x)log⁡v(x)=−1m∑i=1m⟮∑xu(x∣w1,…,wi−1)log⁡p(x∣w1,…,wi−1)⟯=−1m∑i=1mlog⁡p(wi∣w1,…,wi−1)=log⁡(ppl(S))\begin{split} H(u,v) = &-\sum_x u(x) \log v(x) \\ = & - \frac{1}{m} \sum_{i = 1}^m \lgroup \sum_{x} u(x \mid w_1,\dots, w_{i -1}) \log p(x \mid w_1, \dots,w_{i-1}) \rgroup \\ = & -\frac{1}{m} \sum_{i = 1}^m \log p(w_i \mid w_1,\dots,w_{i-1}) \\ = & \log (ppl(S)) \end{split}