本文是一篇关于主题建模及其相关技术的综述。文中介绍了四种最流行的技术,用于探讨主题建模,它们分别是:LSA、pLSA、LDA,以及最新的、基于深度学习的 lda2vec。
在自然语言理解任务中,我们可以通过一系列的层次来提取含义——从单词、句子、段落,再到文档。在文档层面,理解文本最有效的方式之一就是分析其主题。在文档集合中学习、识别和提取这些主题的过程被称为主题建模。
在本文中,我们将通过 4 种最流行的技术来探讨主题建模,它们分别是:LSA、pLSA、LDA,以及最新的、基于深度学习的 lda2vec。
概述
所有主题模型都基于相同的基本假设:
- 每个文档包含多个主题;
- 每个主题包含多个单词。
换句话说,主题模型围绕着以下观点构建:实际上,文档的语义由一些我们所忽视的隐变量或「潜」变量管理。因此,主题建模的目标就是揭示这些潜在变量——也就是主题,正是它们塑造了我们文档和语料库的含义。这篇博文将继续深入不同种类的主题模型,试图建立起读者对不同主题模型如何揭示这些潜在主题的认知。
LSA
潜在语义分析(LSA)是主题建模的基础技术之一。其核心思想是把我们所拥有的文档-术语矩阵分解成相互独立的文档-主题矩阵和主题-术语矩阵。
第一步是生成文档-术语矩阵。如果在词汇表中给出 m 个文档和 n 个单词,我们可以构造一个 m×n 的矩阵 A,其中每行代表一个文档,每列代表一个单词。在 LSA 的最简单版本中,每一个条目可以简单地是第 j 个单词在第 i 个文档中出现次数的原始计数。然而,在实际操作中,原始计数的效果不是很好,因为它们无法考虑文档中每个词的权重。例如,比起「test」来说,「nuclear」这个单词也许更能指出给定文章的主题。
因此,LSA 模型通常用 tf-idf 得分代替文档-术语矩阵中的原始计数。tf-idf,即词频-逆文本频率指数,为文档 i 中的术语 j 分配了相应的权重,如下所示:
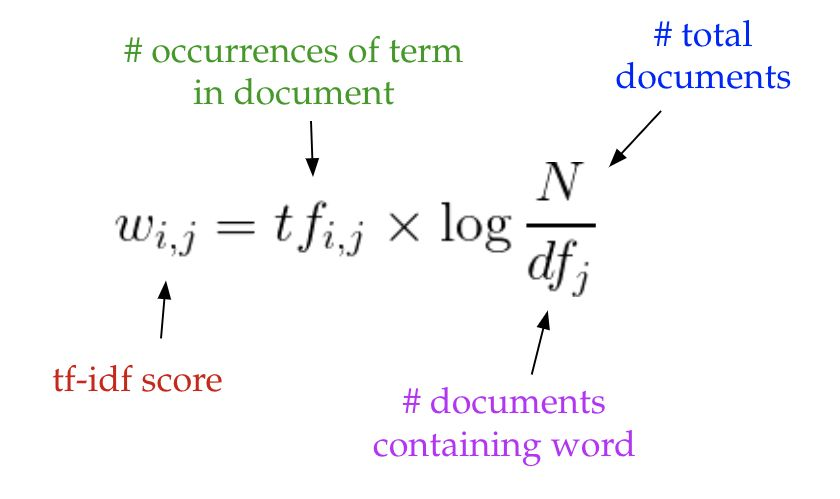
直观地说,术语出现在文档中的频率越高,则其权重越大;同时,术语在语料库中出现的频率越低,其权重越大。
一旦拥有文档-术语矩阵 A,我们就可以开始思考潜在主题。问题在于:A 极有可能非常稀疏、噪声很大,并且在很多维度上非常冗余。因此,为了找出能够捕捉单词和文档关系的少数潜在主题,我们希望能降低矩阵 A 的维度。
这种降维可以使用截断 SVD 来执行。SVD,即奇异值分解,是线性代数中的一种技术。该技术将任意矩阵 M 分解为三个独立矩阵的乘积:M=USV,其中 S 是矩阵 M 奇异值的对角矩阵。很大程度上,截断 SVD 的降维方式是:选择奇异值中最大的 t 个数,且只保留矩阵 U 和 V 的前 t 列。在这种情况下,t 是一个超参数,我们可以根据想要查找的主题数量进行选择和调整。
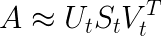
直观来说,截断 SVD 可以看作只保留我们变换空间中最重要的 t 维。

在这种情况下,U∈ℝ^(m⨉t)是我们的文档-主题矩阵,而 V∈ℝ^(n⨉t)则成为我们的术语-主题矩阵。在矩阵 U 和 V 中,每一列对应于我们 t 个主题当中的一个。在 U 中,行表示按主题表达的文档向量;在 V 中,行代表按主题表达的术语向量。
通过这些文档向量和术语向量,现在我们可以轻松应用余弦相似度等度量来评估以下指标:
- 不同文档的相似度
- 不同单词的相似度
- 术语(或「queries」)与文档的相似度(当我们想要检索与查询最相关的段落,即进行信息检索时,这一点将非常有用)
案例
在 sklearn 中,LSA 的简单实现可能如下所示:
1 | from sklearn.feature_extraction.text import TfidfVectorizer |
LSA 方法快速且高效,但它也有一些主要缺点:
- 缺乏可解释的嵌入(我们并不知道主题是什么,其成分可能积极或消极,这一点是随机的)
- 需要大量的文件和词汇来获得准确的结果
- 表征效率低
PLSA
pLSA,即概率潜在语义分析,采取概率方法替代 SVD 以解决问题。其核心思想是找到一个潜在主题的概率模型,该模型可以生成我们在文档-术语矩阵中观察到的数据。特别是,我们需要一个模型 P(D,W),使得对于任何文档 d 和单词 w,P(d,w) 能对应于文档-术语矩阵中的那个条目。
让我们回想主题模型的基本假设:每个文档由多个主题组成,每个主题由多个单词组成。pLSA 为这些假设增加了概率自旋:
- 给定文档 d,主题 z 以 P(z|d) 的概率出现在该文档中
- 给定主题 z,单词 w 以 P(w|z) 的概率从主题 z 中提取出来
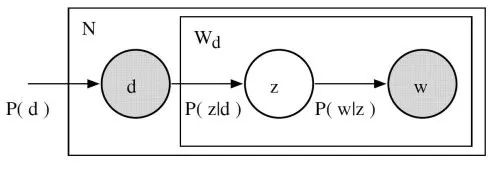
从形式上看,一个给定的文档和单词同时出现的联合概率是:
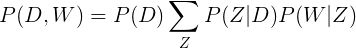
直观来说,等式右边告诉我们理解某个文档的可能性有多大;然后,根据该文档主题的分布情况,在该文档中找到某个单词的可能性有多大。
在这种情况下,P(D)、P(Z|D)、和 P(W|Z) 是我们模型的参数。P(D) 可以直接由我们的语料库确定。P(Z|D) 和 P(W|Z) 利用了多项式分布建模,并且可以使用期望最大化算法(EM)进行训练。EM 无需进行算法的完整数学处理,而是一种基于未观测潜变量(此处指主题)的模型找到最可能的参数估值的方法。
有趣的是,P(D,W) 可以利用不同的的 3 个参数等效地参数化:
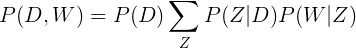
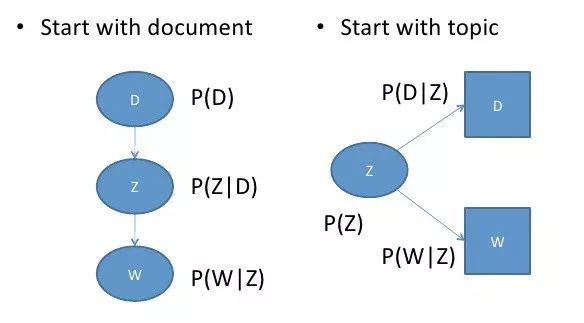
可以通过将模型看作一个生成过程来理解这种等价性。在第一个参数化过程中,我们从概率为 P(d) 的文档开始,然后用 P(z|d) 生成主题,最后用 P(w|z) 生成单词。而在上述这个参数化过程中,我们从 P(z) 开始,再用 P(d|z) 和 P(w|z) 单独生成文档。
这个新参数化方法非常有趣,因为我们可以发现 pLSA 模型和 LSA 模型之间存在一个直接的平行对应关系:
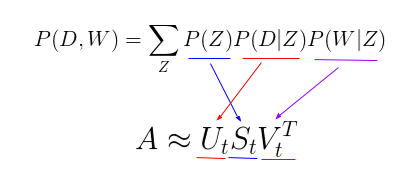
其中,主题 P(Z) 的概率对应于奇异主题概率的对角矩阵,给定主题 P(D|Z) 的文档概率对应于文档-主题矩阵 U,给定主题 P(W|Z) 的单词概率对应于术语-主题矩阵 V。
那么,这说明了什么?尽管 pLSA 看起来与 LSA 差异很大、且处理问题的方法完全不同,但实际上 pLSA 只是在 LSA 的基础上添加了对主题和词汇的概率处理罢了。pLSA 是一个更加灵活的模型,但仍然存在一些问题,尤其表现为:
- 因为我们没有参数来给 P(D) 建模,所以不知道如何为新文档分配概率
- pLSA 的参数数量随着我们拥有的文档数线性增长,因此容易出现过度拟合问题
我们将不会考虑任何 pLSA 的代码,因为很少会单独使用 pLSA。一般来说,当人们在寻找超出 LSA 基准性能的主题模型时,他们会转而使用 LDA 模型。LDA 是最常见的主题模型,它在 pLSA 的基础上进行了扩展,从而解决这些问题。
LDA
LDA 即潜在狄利克雷分布,是 pLSA 的贝叶斯版本。它使用狄利克雷先验来处理文档-主题和单词-主题分布,从而有助于更好地泛化。
我不打算深入讲解狄利克雷分布,不过,我们可以对其做一个简短的概述:即,将狄利克雷视为「分布的分布」。本质上,它回答了这样一个问题:「给定某种分布,我看到的实际概率分布可能是什么样子?」
考虑比较主题混合概率分布的相关例子。假设我们正在查看的语料库有着来自 3 个完全不同主题领域的文档。如果我们想对其进行建模,我们想要的分布类型将有着这样的特征:它在其中一个主题上有着极高的权重,而在其他的主题上权重不大。如果我们有 3 个主题,那么我们看到的一些具体概率分布可能会是:
- 混合 X:90% 主题 A,5% 主题 B,5% 主题 C
- 混合 Y:5% 主题 A,90% 主题 B,5% 主题 C
- 混合 Z:5% 主题 A,5% 主题 B,90% 主题 C
如果从这个狄利克雷分布中绘制一个随机概率分布,并对单个主题上的较大权重进行参数化,我们可能会得到一个与混合 X、Y 或 Z 非常相似的分布。我们不太可能会抽样得到这样一个分布:33%的主题 A,33%的主题 B 和 33%的主题 C。
本质上,这就是狄利克雷分布所提供的:一种特定类型的抽样概率分布法。我们可以回顾一下 pLSA 的模型:
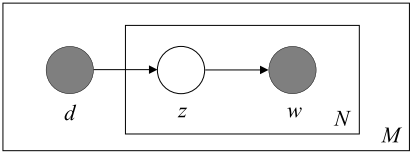
在 pLSA 中,我们对文档进行抽样,然后根据该文档抽样主题,再根据该主题抽样一个单词。以下是 LDA 的模型:
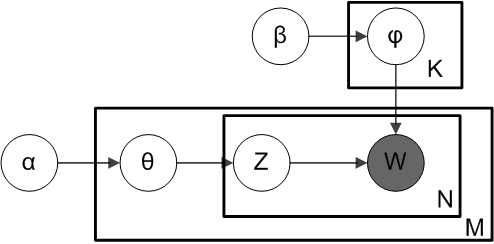
根据狄利克雷分布 Dir(α),我们绘制一个随机样本来表示特定文档的主题分布或主题混合。这个主题分布记为θ。我们可以基于分布从θ选择一个特定的主题 Z。
接下来,从另一个狄利克雷分布 Dir(𝛽),我们选择一个随机样本来表示主题 Z 的单词分布。这个单词分布记为φ。从φ中,我们选择单词 w。
从形式上看,从文档生成每个单词的过程如下(注意,该算法使用 c 而不是 z 来表示主题):

通常而言,LDA 比 pLSA 效果更好,因为它可以轻而易举地泛化到新文档中去。在 pLSA 中,文档概率是数据集中的一个固定点。如果没有看到那个文件,我们就没有那个数据点。然而,在 LDA 中,数据集作为训练数据用于文档-主题分布的狄利克雷分布。即使没有看到某个文件,我们可以很容易地从狄利克雷分布中抽样得来,并继续接下来的操作。
代码实现
LDA 无疑是最受欢迎(且通常来说是最有效的)主题建模技术。它在 gensim 当中可以方便地使用:
1 | from gensim.corpora.Dictionary import load_from_text, doc2bow |
通过使用 LDA,我们可以从文档语料库中提取人类可解释的主题,其中每个主题都以与之关联度最高的词语作为特征。例如,主题 2 可以用诸如「石油、天然气、钻井、管道、楔石、能量」等术语来表示。此外,在给定一个新文档的条件下,我们可以获得表示其主题混合的向量,例如,5% 的主题 1,70% 的主题 2,10%的主题 3 等。通常来说,这些向量对下游应用非常有用。
深度学习中的 LDA:lda2vec
那么,这些主题模型会将哪些因素纳入更复杂的自然语言处理问题中呢?
在文章的开头,我们谈到能够从每个级别的文本(单词、段落、文档)中提取其含义是多么重要。在文档层面,我们现在知道如何将文本表示为主题的混合。在单词级别上,我们通常使用诸如 word2vec 之类的东西来获取其向量表征。lda2vec 是 word2vec 和 LDA 的扩展,它共同学习单词、文档和主题向量。
原理
lda2vec 专门在 word2vec 的 skip-gram 模型基础上建模,以生成单词向量。skip-gram 和 word2vec 本质上就是一个神经网络,通过利用输入单词预测周围上下文词语的方法来学习词嵌入。
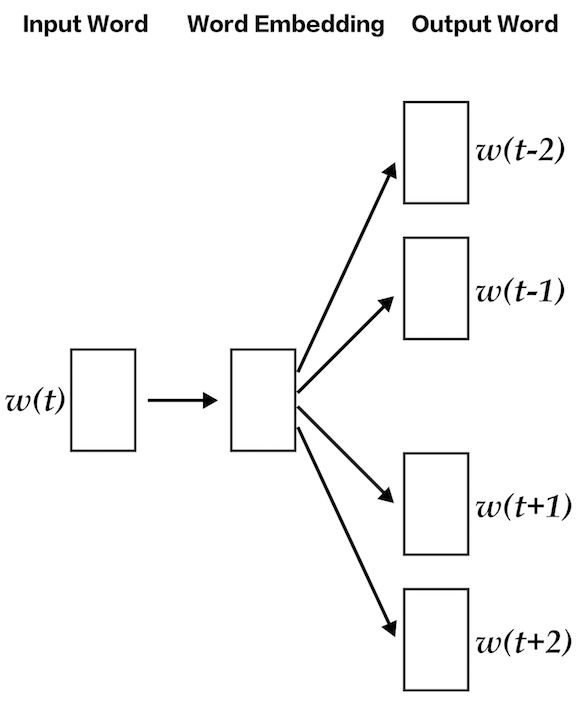
通过使用 lda2vec,我们不直接用单词向量来预测上下文单词,而是使用上下文向量来进行预测。该上下文向量被创建为两个其它向量的总和:单词向量和文档向量。
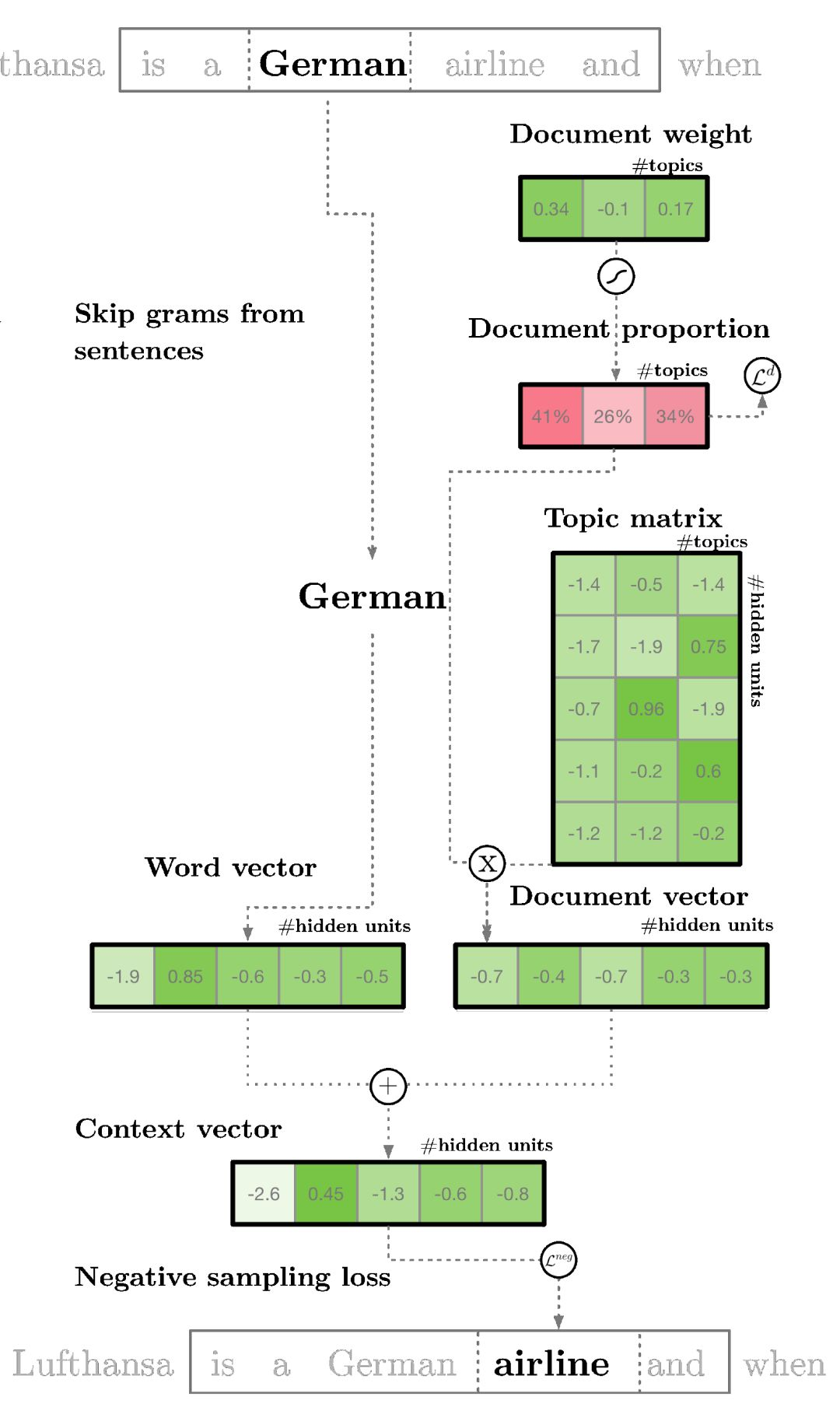
单词向量由前面讨论过的 skip-gram word2vec 模型生成。而文档向量更有趣,它实际上是下列两个组件的加权组合:
- 文档权重向量,表示文档中每个主题的「权重」(稍后将转换为百分比)
- 主题矩阵,表示每个主题及其相应向量嵌入
文档向量和单词向量协同起来,为文档中的每个单词生成「上下文」向量。lda2vec 的强大之处在于,它不仅能学习单词的词嵌入(和上下文向量嵌入),还同时学习主题表征和文档表征。
- 博客地址:https://multithreaded.stitchfix.com/blog/2016/05/27/lda2vec/#topic=38&lambda=1&term=
- 代码地址:https://github.com/cemoody/lda2vec
总结
我们常把主题模型当作「有点用处」的黑箱算法。幸运的是,与许多神经网络算法不同,主题模型实际上是可解释的,它可以更直接地进行诊断、调整和评估。希望这篇博文能够解释基础数学知识、内在驱动力和你所需要的直觉。
原文链接:https://medium.com/nanonets/topic-modeling-with-lsa-psla-lda-and-lda2vec-555ff65b0b05