【速读】：该论文试图解决SFT与RL在LLM推理任务中的最优整合问题。核心洞察是：SFT对策略分布进行粗粒度全局调整，而RL进行细粒度选择性优化；熵可作为训练有效性的关键指标。解决方案是SRFT——一种单阶段方法，通过熵感知权重机制统一SFT和RL，同时利用演示数据和自探索rollout直接优化LLM。
【机构】：中国科学院自动化研究所（Institute of Automation, Chinese Academy of Sciences）；中国科学院大学人工智能学院（School of Artificial Intelligence, University of Chinese Academy of Sciences）；美团（Meituan）；上海交通大学（Shanghai Jiao Tong University）
【开源】：模型已开源至 https://huggingface.co/Yuqian-Fu/SRFT

1. 背景与核心洞察 (The Core Insight)

大语言模型在推理任务上的进展令人瞩目，但如何最优地整合监督微调（SFT）与强化学习（RL）仍是一个根本性的挑战。传统做法通常将SFT和RL视为两个独立的顺序阶段——先用SFT进行指令跟随训练，再用RL进行对齐优化。然而，这种分离带来了诸多问题：SFT可能导致模型仅记忆模式而缺乏真正的推理能力，容易过拟合训练数据；而RL虽然具有探索和奖励优化的潜力，却面临样本效率低、在巨大解空间中难以有效探索、以及模式崩溃（重复生成相似的次优输出）等问题。

近期工作开始探索将SFT和RL统一在集成框架中，或在训练过程中动态切换两种微调方法。这引出了一个关键问题：如何确定SFT知识蒸馏与RL策略优化之间的平衡？整合不足可能导致错误传播并限制RL的改进空间，而过度依赖演示数据则会导致过拟合，限制策略在基础分布之外的探索。

本文通过全面的token分布分析、学习动态分析和基于熵的整合机制研究，揭示了SFT和RL的本质差异：

  • SFT 对LLM策略分布进行粗粒度全局改变
  • RL 执行细粒度选择性优化
  • 熵 是训练有效性的关键指标

基于这些观察，作者提出SRFT（Supervised Reinforcement Fine-Tuning），一种单阶段方法，通过熵感知权重机制统一两种微调范式，同时应用SFT和RL直接优化LLM，而非通过两阶段顺序方法。

2. 技术方案深度拆解 (The “How”)

2.1 核心机制：SFT vs. RL 的本质差异

Token分布效应分析

论文通过可视化微调前后的token概率变化，揭示了SFT和RL的根本差异：

  • SFT：在整个响应序列上大幅改变概率分布，token概率变化幅度大且分布广泛
  • RL：仅选择性修改一小部分token的概率，数值内容和数学证明陈述基本保持不变

从理论角度，SFT的梯度可表示为：

∇θLSFT=E(x,y)∼D[∑t=1∣y∣∑v∈V(πθ(v∣x,y<t)−1v=yt)∇θlog⁡πθ(v∣x,y<t)]\nabla_\theta \mathcal{L}_{\text{SFT}} = \mathbb{E}_{(\bm{x}, \bm{y}) \sim \mathcal{D}} \left[ \sum_{t=1}^{|\bm{y}|} \sum_{v \in \mathcal{V}} \left( \pi_\theta(v|\bm{x}, \bm{y}_{<t}) - \mathbf{1}_{v = y_t} \right) \nabla_\theta \log \pi_\theta(v|\bm{x}, \bm{y}_{<t}) \right]

解析：SFT通过增加目标token的概率同时降低词汇表中所有其他token的概率来系统地锐化模型分布，导致输出更加确定性。

学习动态可视化

论文提出了一种新颖的可视化方法，将每个模型映射到词汇概率空间中的一个点，以三个参考模型（Qwen-2.5-Math-7B基础模型、DeepSeek-R1、QwQ-32B）作为坐标框架：

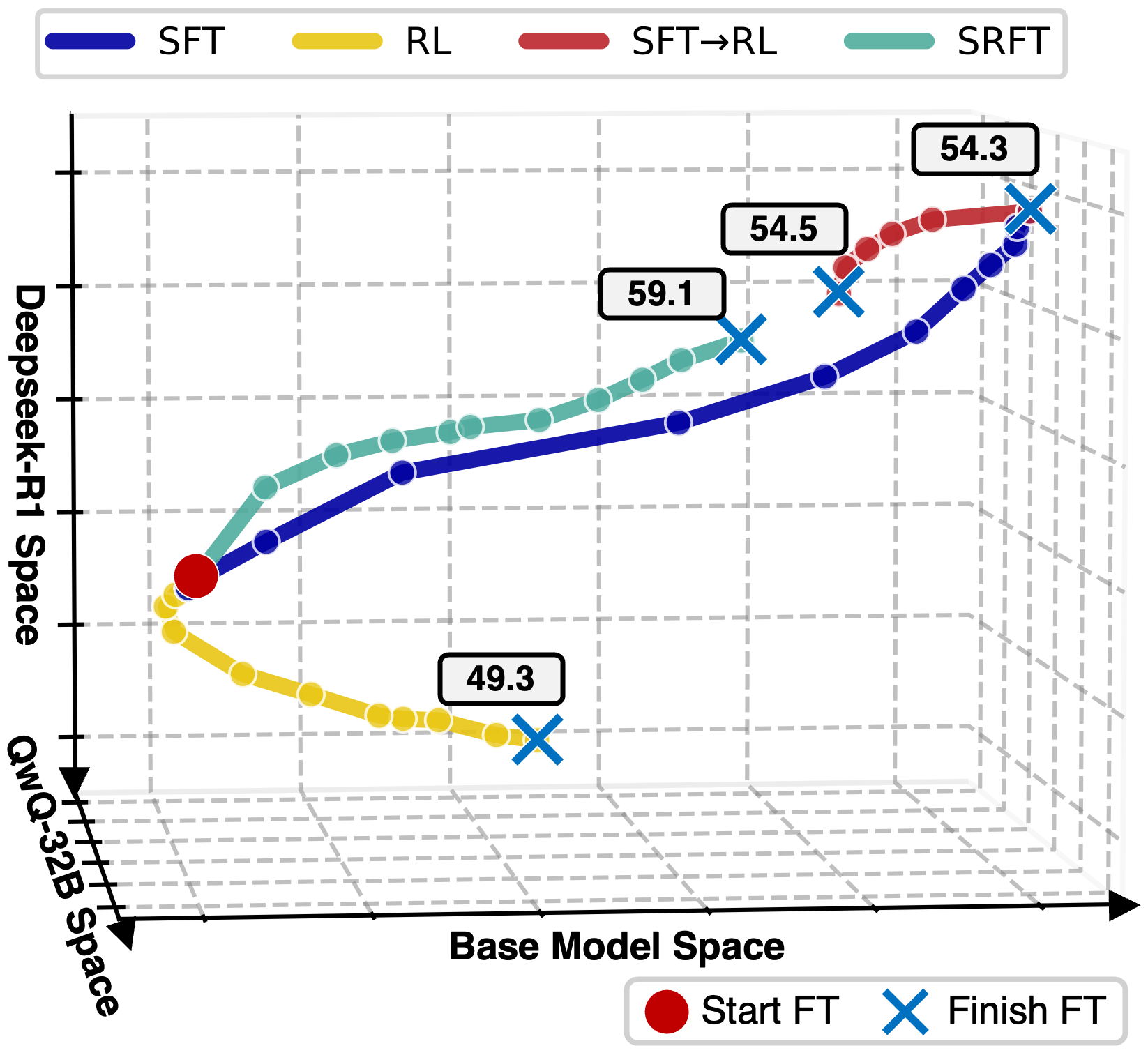
关键发现：

  • SFT相比RL表现出更大的分布变化，且性能更高
  • 两阶段SFT→RL方法的学习动态从SFT后模型向更高性能区域移动，但 paradoxically 更接近基础模型
  • 单阶段SRFT方法在概率空间中表现出更受约束且目标明确的变化

2.2 熵作为整合指标

通过对比SFT→RL和RL→SFT两种顺序整合策略，论文发现：

  • RL→SFT 在所有基准上 consistently 产生次优性能
  • SFT→RL 成功实现显著性能提升

从熵的角度分析：

  • RL后的策略表现出显著更低的熵，接近确定性输出
  • 后续SFT引入的分布偏移导致熵快速增加（对应性能急剧下降），随后逐渐下降
  • RL后的模型通过SFT进一步学习的能力有限，约90步后出现熵平台期
  • 基础模型经历SFT时表现出短暂的初始熵增加后持续下降，最终带来性能提升

这表明熵是SFT和RL有效整合的关键指标。

2.3 SRFT架构

SRFT的核心创新在于单阶段学习机制：通过SFT进行粗粒度行为策略近似，通过RL进行细粒度策略精炼，两者同时应用于演示数据和自生成的试错数据。

从演示数据学习：

SRFT采用双管齐下的策略利用演示数据（如DeepSeek-R1生成的推理响应）：

  1. SFT组件：执行行为策略的粗粒度近似

LSFTdemo.=E(x,y)∼Ddemo.[−log⁡πθ(y∣x)]\mathcal{L}^{\text{demo.}}_{\text{SFT}}=\mathbb{E}_{(\bm{x}, \bm{y}) \sim \mathcal{D}_\text{demo.}}[-\log \pi_{\theta}(\bm{y}|\bm{x})]

引入熵感知权重机制：

wSFT=0.5⋅stop_grad(exp⁡(−H(πθ)))w_\text{SFT} = 0.5 \cdot \texttt{stop\_grad}(\exp(-\mathcal{H}(\pi_{\theta})))

LSFTdemo.(θ)=wSFT⋅E(x,y)∼Ddemo.[−log⁡πθ(y∣x)]\mathcal{L}_{\text{SFT}}^{\text{demo.}}(\theta) = w_\text{SFT} \cdot \mathbb{E}_{(\bm{x}, \bm{y}) \sim \mathcal{D}_{\text{demo.}}}[-\log \pi_{\theta}(\bm{y}|\bm{x})]

解析：当策略表现出高熵（不确定性）时，SFT训练损失对模型更新的影响减弱，从而缓解演示数据行为策略与当前策略之间分布不匹配导致的性能下降。

  1. RL组件：通过off-policy RL进行行为策略的细粒度学习

将演示数据直接增强到LLM的on-policy rollout组中：

Gaug.={(xi,yi)}i=1∣Groll.∣∪{(xj,yj)}j=1∣Gdemo.∣G_{\text{aug.}} = \{(\bm{x}_i, \bm{y}_i)\}_{i=1}^{|G_{\text{roll.}}|} \cup \{(\bm{x}_j, \bm{y}_j)\}_{j=1}^{|G_{\text{demo.}}|}

优势估计：

A^k=r(x,yk)−mean({r(x,yk)∣k=1,2,…,∣Gaug.∣})std({r(x,yk)∣k=1,2,…,∣Gaug.∣})\hat{A}_k = \frac{r(\bm{x}, \bm{y}_k) - \text{mean}(\{r(\bm{x}, \bm{y}_k)|k=1,2,\ldots,|G_{\text{aug.}}|\})}{\text{std}(\{r(\bm{x}, \bm{y}_k)|k=1,2,\ldots,|G_{\text{aug.}}|\})}

从自探索Rollout学习：

在on-policy RL与二元奖励 {1,−1}\{1, -1\} 下，基本RL目标函数可自然分解为两个组件：

LRLself-rollout=Ex∼D,y+∼πθ(⋅∣x)[−log⁡πθ(y+∣x)]⏟正样本+Ex∼D,y−∼πθ(⋅∣x)[log⁡πθ(y−∣x)]⏟负样本\mathcal{L}_{\text{RL}}^{\text{self-rollout}} = \underbrace{\mathbb{E}_{\bm{x}\sim \mathcal{D},\bm{y}^+ \sim \pi_{\theta}(\cdot|\bm{x})} [-\log \pi_{\theta}(\bm{y}^+|\bm{x})]}_{\text{正样本}} + \underbrace{\mathbb{E}_{\bm{x}\sim \mathcal{D},\bm{y}^- \sim \pi_{\theta}(\cdot|\bm{x})} [\log \pi_{\theta}(\bm{y}^-|\bm{x})]}_{\text{负样本}}

关键洞察：正样本目标在结构上与监督微调相似，但这些正样本是由当前策略πθ\pi_{\theta} on-policy生成的，而非来自SFT数据集。

为缓解自探索导致的快速熵降低，引入针对正样本目标的熵自适应权重机制：

wRL=0.1⋅stop_grad(exp⁡(H(πθ)))w_\text{RL} = 0.1 \cdot \texttt{stop\_grad}(\exp(\mathcal{H}(\pi_{\theta})))

LRLself-rollout(θ)=wRL⋅Ex∼D,y+∼πθ(⋅∣x)[−log⁡πθ(y+∣x)]+Ex∼D,y−∼πθ(⋅∣x)[log⁡πθ(y−∣x)]\mathcal{L}_{\text{RL}}^{\text{self-rollout}}(\theta) = w_\text{RL} \cdot \mathbb{E}_{\bm{x}\sim \mathcal{D},\bm{y}^+ \sim \pi_{\theta}(\cdot|\bm{x})} [-\log \pi_{\theta}(\bm{y}^+|\bm{x})] + \mathbb{E}_{\bm{x}\sim \mathcal{D},\bm{y}^- \sim \pi_{\theta}(\cdot|\bm{x})} [\log \pi_{\theta}(\bm{y}^-|\bm{x})]

总目标函数：

LSRFT(θ)=LSFTdemo.(θ)+LRLdemo.(θ)+LRLself-rollout(θ)\mathcal{L}_{\text{SRFT}}(\theta) = \mathcal{L}_{\text{SFT}}^{\text{demo.}}(\theta) + \mathcal{L}_{\text{RL}}^{\text{demo.}}(\theta) + \mathcal{L}_{\text{RL}}^{\text{self-rollout}}(\theta)

3. 验证与实验分析 (Evidence & Analysis)

3.1 主实验结果

在五个竞赛级数学推理基准（AIME24、AMC、MATH500、Minerva、Olympiad）和三个分布外基准（ARC-C、GPQA-D、MMLU-Pro）上的评估结果：

方法 AIME24 AMC MATH500 Minerva Olympiad 平均 ARC-C GPQA-D MMLU-Pro OOD平均
Qwen2.5-Math 11.4 32.6 48.8 8.7 15.8 23.5 18.2 11.1 16.9 15.4
SFT 31.1 62.8 85.2 39.1 53.3 54.3 76.2 25.8 45.7 49.2
RL_GRPO 24.7 61.6 79.2 33.7 47.1 49.3 75.6 31.3 42.1 49.7
SFT→RL 32.5 67.1 84.2 34.1 54.6 54.5 76.4 37.9 49.6 54.6
LUFFY 29.4 65.6 87.6 37.5 57.2 55.5 80.5 39.9 53.0 57.8
SRFT 35.3 74.3 89.8 39.7 58.3 59.5 85.3 46.4 55.9 62.5

关键发现：

  • SRFT在五个数学推理基准上达到59.5%平均准确率，比最佳zero-RL基线提升+9.0个百分点
  • 相比SFT方法提升**+4.8**个百分点，表明自探索组件能有效精炼从演示中学到的策略分布
  • 相比SFT+RL方法提升**+3.4**个百分点，证明单阶段设计和熵感知机制能有效平衡演示和自探索的收益
  • 在分布外基准上达到62.5%平均得分，比最佳基线提升+4.7个百分点

3.2 训练动态分析

训练奖励（左图）：SRFT相比RL实现更快的性能提升，两者都表现出训练奖励的上升趋势。

响应长度（中图）：面对挑战性训练数据时，RL倾向于生成更简洁的响应，而SRFT表现出响应长度逐渐增加，表明发展了更 thorough 和详细的推理过程。

训练熵（右图）：与RL表现出的快速熵下降相比，SRFT保持更稳定的熵，表明策略能在训练期间持续探索，这也证明了熵感知权重机制的有效性。

3.3 消融实验

模型 AIME24 AMC MATH-500 Minerva Olympiad 平均
Qwen2.5-Math 11.4 32.6 48.8 8.7 15.8 23.5
SRFT w/o wSFTw_\text{SFT} 30.1 65.8 87.0 36.8 55.8 55.1
SRFT w/o wRLw_\text{RL} 32.6 67.2 87.5 37.4 56.5 56.2
SRFT 35.3 72.2 89.8 39.7 58.3 59.1

移除SFT权重机制导致性能下降**-4.0个百分点，移除RL权重导致-2.9**个百分点的下降，证明两个组件对整体性能都有显著贡献。

3.4 SFT-RL整合策略对比

模型 AIME24 AMC MATH500 Minerva Olympiad 平均
Qwen2.5-Math-7B 14.1 44.8 64.8 16.5 29.6 34.0
SFT 21.2 53.2 83.0 37.1 42.2 47.3
RL 21.2 59.3 83.6 36.4 46.6 49.4
RL→SFT 10.5 40.4 73.6 32.0 30.7 37.4
RL→SFT_KL 13.1 45.2 70.2 26.5 36.3 38.3
SFT→RL 24.5 59.3 86.4 39.3 53.1 52.5

RL→SFT consistently 产生次优性能，即使引入KL散度约束，性能提升仍然有限。这种不对称行为揭示了微调范式序列对最终模型性能的关键影响。

4. 局限性与落地思考 (Critical Review)

复现门槛：

  • 实验基于64张A100 GPU进行，对算力要求较高
  • 使用OpenR1-Math-46k-8192数据集，包含DeepSeek-R1生成的高质量推理响应，需要访问此类高质量演示数据
  • 将RoPE theta从10,000增加到40,000并扩展窗口大小到16,384，需要特定的模型配置调整

潜在短板：

  • 当前对熵动态的利用相对简单，仅使用基本指数权重函数。熵在训练期间的丰富时间模式暗示了更复杂的基于熵的控制机制的潜力
  • 方法假设可以访问高质量演示数据，对于无法获得此类数据的场景适用性有限
  • 论文未深入探讨不同质量演示数据对方法的影响

工程落地启发：

  • 熵监控：在实际训练中监控策略熵的变化可作为训练稳定性的早期预警指标
  • 动态权重：SRFT的熵感知权重机制可推广到其他SFT-RL混合训练场景
  • 单阶段优势：相比两阶段训练，单阶段方法减少了训练流程复杂性，更适合生产环境部署

5. 总结与启示 (The Verdict)

对研发的启示：

  1. SFT与RL的本质差异：SFT是"大锤"（粗粒度全局调整），RL是"手术刀"（细粒度选择性优化）。理解这一差异有助于设计更精细的训练策略。

  2. 熵作为训练指标：熵不仅是理论概念，更是可操作的训练监控指标。高熵区域适合SFT引导，低熵区域需要谨慎处理以避免过度确定性。

  3. 单阶段训练的价值：SRFT证明SFT和RL可以在单阶段中有效整合，避免了顺序训练中的灾难性遗忘问题，同时提高了训练效率。

待澄清疑点：

  1. 演示数据质量边界：论文假设使用DeepSeek-R1生成的高质量演示数据，但未测试次优演示数据对方法的影响。在实际应用中，演示数据的质量参差不齐，SRFT对此的鲁棒性需要进一步验证。

  2. 熵权重函数的选择：wSFT=0.5⋅exp⁡(−H)w_\text{SFT} = 0.5 \cdot \exp(-\mathcal{H}) 和 wRL=0.1⋅exp⁡(H)w_\text{RL} = 0.1 \cdot \exp(\mathcal{H}) 中的系数（0.5和0.1）是否对不同模型规模/任务具有通用性？论文未提供详细的超参数敏感性分析。

  3. 长期训练动态：实验仅进行500步训练，对于更长训练周期的熵动态变化和性能收敛行为尚不清楚。

  4. 与其他RL算法的兼容性：SRFT基于GRPO构建，其与PPO、DPO等其他RL算法的结合方式有待探索。