Revisiting Self-Training for Few-Shot Learning of Language Model

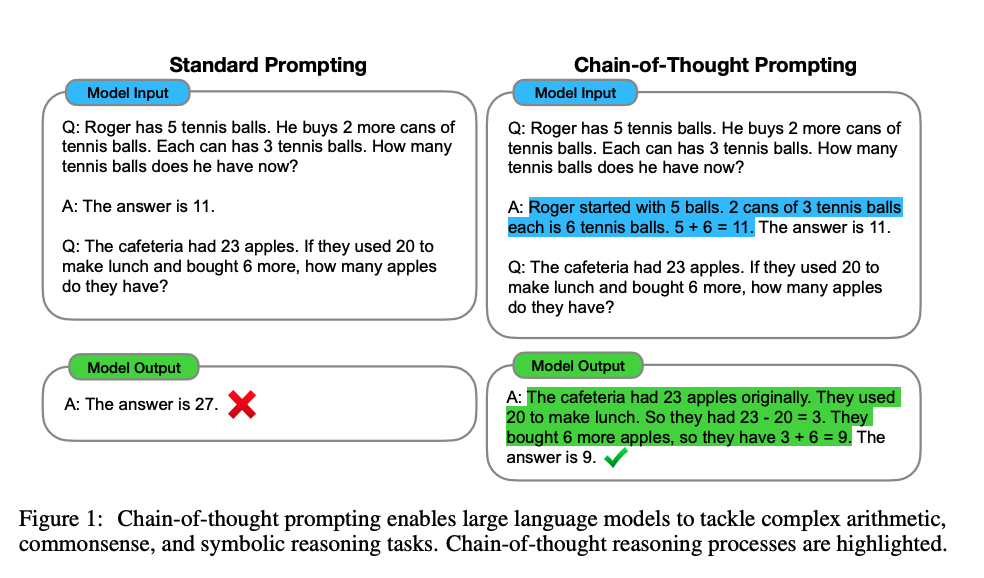
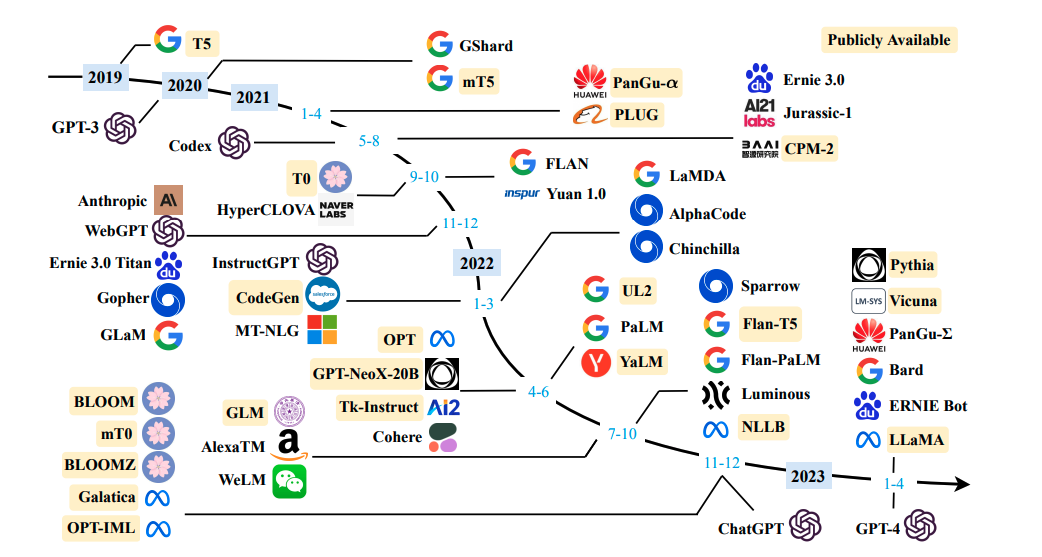
本篇博文我们主要关注prompt模式在半监督学习场景下的应用，特别是针对少量标注和无标注数据。在实际应用环境中，获得高质量的标注数据是比较耗时和昂贵的，往往都是小部分标注数据和大量的无标注数据，半监督学习（Semi-supervised learning，SSL）是一种学习方法，其使用少量标注的数据和大量未标注的数据进行学习，从而得到一个高质量模型。之前prompt应用大部分都是在few-shot下的有监督训练，如LM-BFF，或者结合大量无标注数据下半监督训练，如PET。本文作者提出一种名为SFLM的方法，通过对没有标注的样本（prompt结构）进行弱增强和强增强，首先对弱增强产生的数据通过模型产生伪标签，当模型的预测得分高于一定的阈值时，伪标签作为该样本标签，并与强增强数据模型预测结果进行计算损失。实验结果表明，只依赖于少数领域内的未标注的数据情况下，SFLM在6个句子分类和6个句子对分类基准任务上达到了最好的效果。

论文地址: https://arxiv.org/pdf/2110.01256.pdf

论文源码地址: https://github.com/MatthewCYM/SFLM

方法

本文作者提出的SFLM结构如下所示：

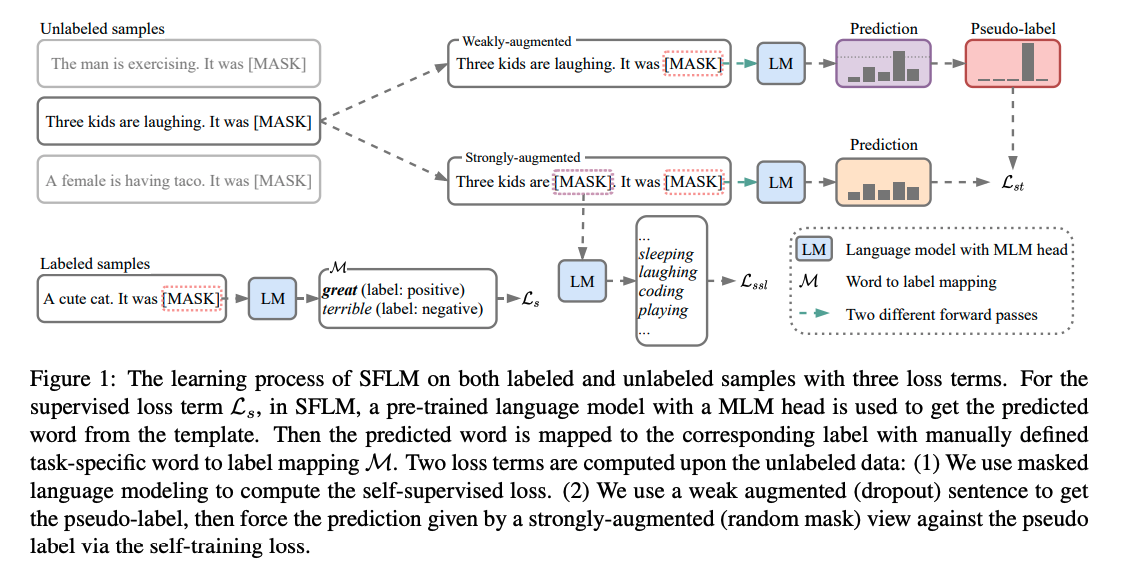
SFLM训练过程包含两部分：有监督训练和无监督训练。对于有标注数据，进行常规的prompt模式有监督训练过程即可，这里我们主要重点介绍无监督训练过程，从上图可以看到，对于每个未标注的样本（prompt形式），使用弱增强和强增强获得对应增强样本。首先，弱增强样本通过模型得到预测得分，当模型的预测得分高于一定的阈值时，对应的类别作为 ground truth 的标签，即伪标签。然后，强增强的样本通过相同模型得到预测得分，并使用交叉熵损失将此预测得分与 ground truth 伪标签进行比较。

SFLM损失包含三部分：有标签的样本用有监督的损失$L_s$，没有标签的样本包含自训练的损失$L_{st}$和自监督的损失$L_{ssl}$， 三个损失都是标准的交叉熵损失。

具体来说，给定一个batch大小的标注数据$\mathcal{X_B}=\left\{\left(x_{i}, y_{i}\right): i \in(1, \ldots, B)\right\}$，无标注数据$\mathcal{U_B}=\left\{u_{i}: i \in\right (1, \ldots, \mu B)\}$，其中$\mu$是标注数据与无标注数据之间的比例大小。

Prompt-based supervised loss

将对应的任务转化为语言模型任务，常见形式如下：

$$p_{m}\left(y_{i} \mid x_{i}\right)=p_{m}\left([\text { MASK }]=\mathcal{M}^{\prime}\left(y_{i} \mid x_{i}^{\text {prompt }}\right)\right.$$

其中$\mathcal{M}^{\prime}$表示标签词映射，$x_{i}^{\text {prompt }}$表示将原始输入转化为prompt形式，例如，对于二分类任务而言，常见prompt形式如下:

$$x_{i}^{p r o m p t}=x_{i} \circ \text { It was [MASK] }$$

则使用常规的交叉熵损失，即：

$$\mathcal{L}_{s}=\frac{1}{B} \sum_{i=1}^{B} H\left(y_{i}, p_{m}\left(y_{i} \mid x_{i}\right)\right)$$

Self-training loss

对于没有标签样本$u_i$。通过弱增强方法$\alpha$，得到样本$\alpha\left(u_{i}\right)$，通过模型得到预测得分$q_{i}=p_{m}\left(y_{i} \mid \alpha\left(u_{i}\right)\right)$，如果伪标签的得分大于一定的阈值（$\tau$，论文中的阈值取0.95）即$\hat{q}_{i}=\arg \max \left(q_{i}\right)$，那么，就用该伪标签和强增强获得的特征计算交叉熵损失，即:

$$\begin{aligned} \mathcal{L}_{s t}=& \frac{1}{\mu B} \sum_{i=1}^{\mu B} \mathbb{1}\left(\max \left(q_{i}\right) \geq \tau\right) \\ & \mathrm{H}\left(\hat{q}_{i}, p_{m}\left(y_{i} \mid \mathcal{A}\left(u_{i}\right)\right)\right) \end{aligned}$$

其中，$\tau$为确定伪标签的阈值。增强方法主要如下：

• 弱增强: 采用dropout方式，弱监督仍然保持原始句子语义。

• 强增强: 采用mask方式，类似mlm中的做法，作者对15%的toekn采用[MASK]代替。

Self-supervised loss

预训练中常见的MLM损失，这里主要针对强增强样本。

最后，SFLM总的损失函数为：

$$\mathcal{L}=\mathcal{L}_{s}+\lambda_{1} \mathcal{L}_{s t}+\lambda_{2} \mathcal{L}_{s s l}$$

其中$\lambda_1$、$\lambda_2$是超参数，用来平衡三个损失函数的。

实验

实验数据

为了证明SFLM的有效性，作者在6个句子分类和6个句子对分类基准任务

实验结果

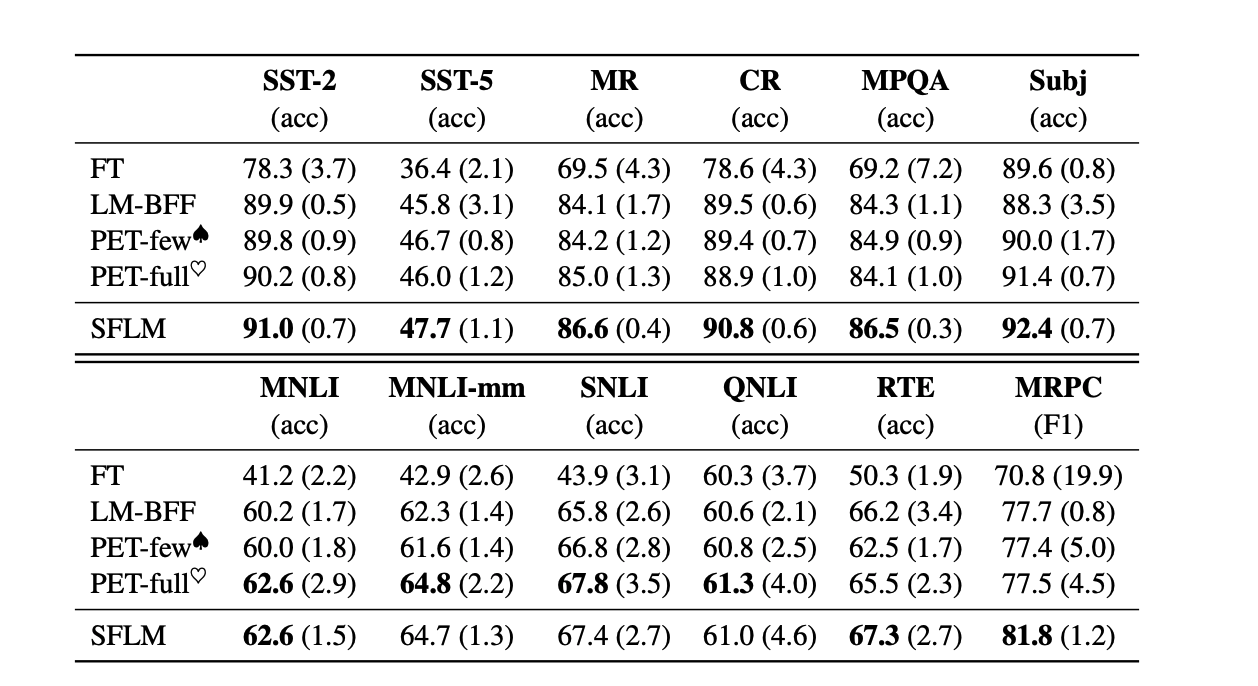
在few-shot实验中，可以看到SFLM在单句子和句子对任务中达到了最好的结果 。

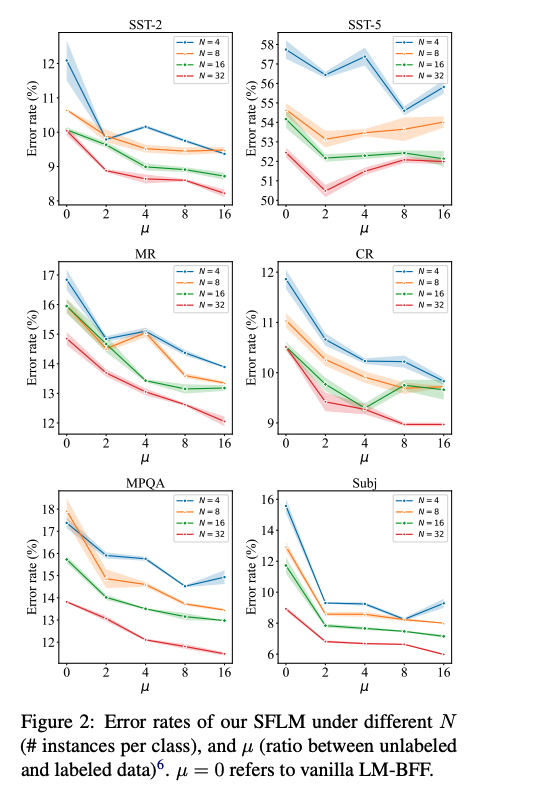
在未标注数据比例实验中，可以看到$\mu$越大，SFLM误差率越低，表明越多的未标注数据，SFLM效果越好，除了SST-5。PET也有类似结果。对于SST-5数据，该任务是六个任务中最难的一个。若模型能力相对较弱，往往自训练方式很难起到作用，一方面模型预测得分低于设定阈值，另一方面伪标签将噪声引入整个训练过程中。

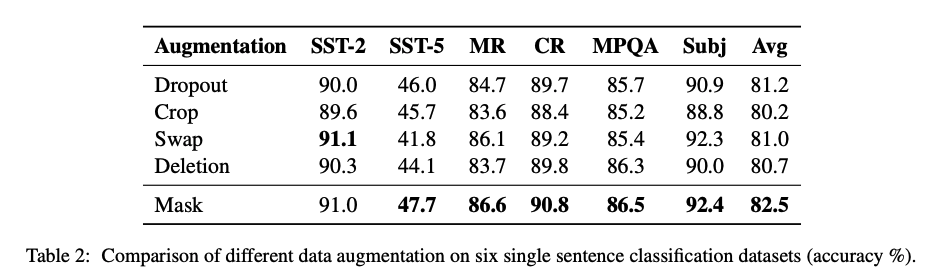
在不同的增强技术实验中，可以看到mask方式是最好的。

小结

本文作者提出一种名为SFLM的方法，通过对没有标注的样本（prompt结构）进行弱增强和强增强，首先对弱增强产生的数据通过模型产生伪标签，当模型的预测得分高于一定的阈值时，伪标签作为该样本标签，并与强增强数据模型预测结果进行计算损失。实验结果表明，只依赖于少数领域内的未标注的数据情况下，SFLM在6个句子分类和6个句子对分类基准任务上达到了最好的效果。