DART：通过梯度隔离解决Agentic RL中推理与工具使用的干扰问题

【速读】：本文揭示了Agentic RL中一个被长期忽视的核心问题——推理（Reasoning）与工具使用（Tool-use）能力在共享参数空间下的联合优化会产生严重的梯度冲突，导致"跷跷板"现象（提升一个能力会损害另一个）。作者提出LEAS（线性效应归因系统）定量验证了这一干扰的存在，并设计了DART框架：通过为两种能力分配独立的LoRA适配器，在token级别进行梯度隔离，从而在单模型内实现与双模型系统相当的性能，同时避免了多Agent系统的存储与推理开销。

【机构】：Renmin University of China（中国人民大学）；Bytedance Inc.（字节跳动）

【开源】：未开源

1. 背景与核心洞察 (The Core Insight)

Agentic Reinforcement Learning（ARL）旨在训练能够交错执行复杂推理与外部工具调用的大语言模型。当前主流范式（如Search-R1、ToolRL等）普遍采用单一共享参数空间来联合优化这两种能力，其隐含的假设是：推理与工具使用可以和谐共存于同一参数子空间，且联合训练能够带来协同增益。

然而，这一假设从未被严格验证。本文通过系统性的实证分析揭示了一个反直觉的现象：推理与工具使用能力之间存在显著的负向交互效应。当模型在共享参数上同时学习这两种能力时，会出现典型的"跷跷板"（Seesaw）现象——提升工具使用能力往往以牺牲推理能力为代价，反之亦然。

这一发现的核心洞察源于对优化动力学的深入分析。作者发现，推理token和工具使用token产生的梯度方向近乎正交（接近90度），这意味着两种能力各自拥有截然不同的最优参数更新方向。当梯度在共享参数空间中被平均时，模型被迫走向一个"折中方向"，该方向对两种能力而言都是次优的。这种梯度冲突构成了ARL的一个根本性优化瓶颈，限制了智能体系统的性能上限。

2. 技术方案深度拆解 (The “How”)

2.1 LEAS：定量验证能力干扰的诊断框架

为了量化推理与工具使用之间的交互效应，作者提出了Linear Effect Attribution System（LEAS），这是一个受方差分解框架启发的诊断工具。

核心设计思想：

将Agent的能力表征为二元指示变量：基础能力 $x_1$ 、工具使用 $x_2$ 、推理 $x_3$
引入交互项 $x_{ij}$ 表示能力 $i$ 和 $j$ 是否被联合优化
模型在问题 $q$ 上的正确率建模为：

$s_{\mathcal{M}}^q = \sigma(\mathbf{x}_{\mathcal{M}}^\top \boldsymbol{\lambda}^q)$

其中 $\lambda_{ij}^q > 0$ 表示协同（synergy）， $\lambda_{ij}^q < 0$ 表示干扰（interference）。

模型变体构造：
LEAS需要6个线性独立的能力配置来求解6维系数向量。作者设计了以下模型变体：

模型	能力配置	构造方式
$\mathcal{M}_{\text{Base}}$	$[1,0,0,0,0,0]$	预训练基座模型
$\mathcal{M}_{\text{Reas}}$	$[1,0,1,0,1,0]$	仅对推理token进行梯度更新
$\mathcal{M}_{\text{Tool}}$	$[1,1,0,1,0,0]$	仅对工具token进行梯度更新
$\mathcal{M}_{\text{Unified}}$	$[1,1,1,1,1,1]$	标准ARL联合训练
$\mathcal{H}_{\text{Tool}}$	$[1,1,0,0,0,0]$	推理用Base，工具用 $\mathcal{M}_{\text{Tool}}$
$\mathcal{H}_{\text{Reas}}$	$[1,0,1,0,0,0]$	推理用 $\mathcal{M}_{\text{Reas}}$ ，工具用Base

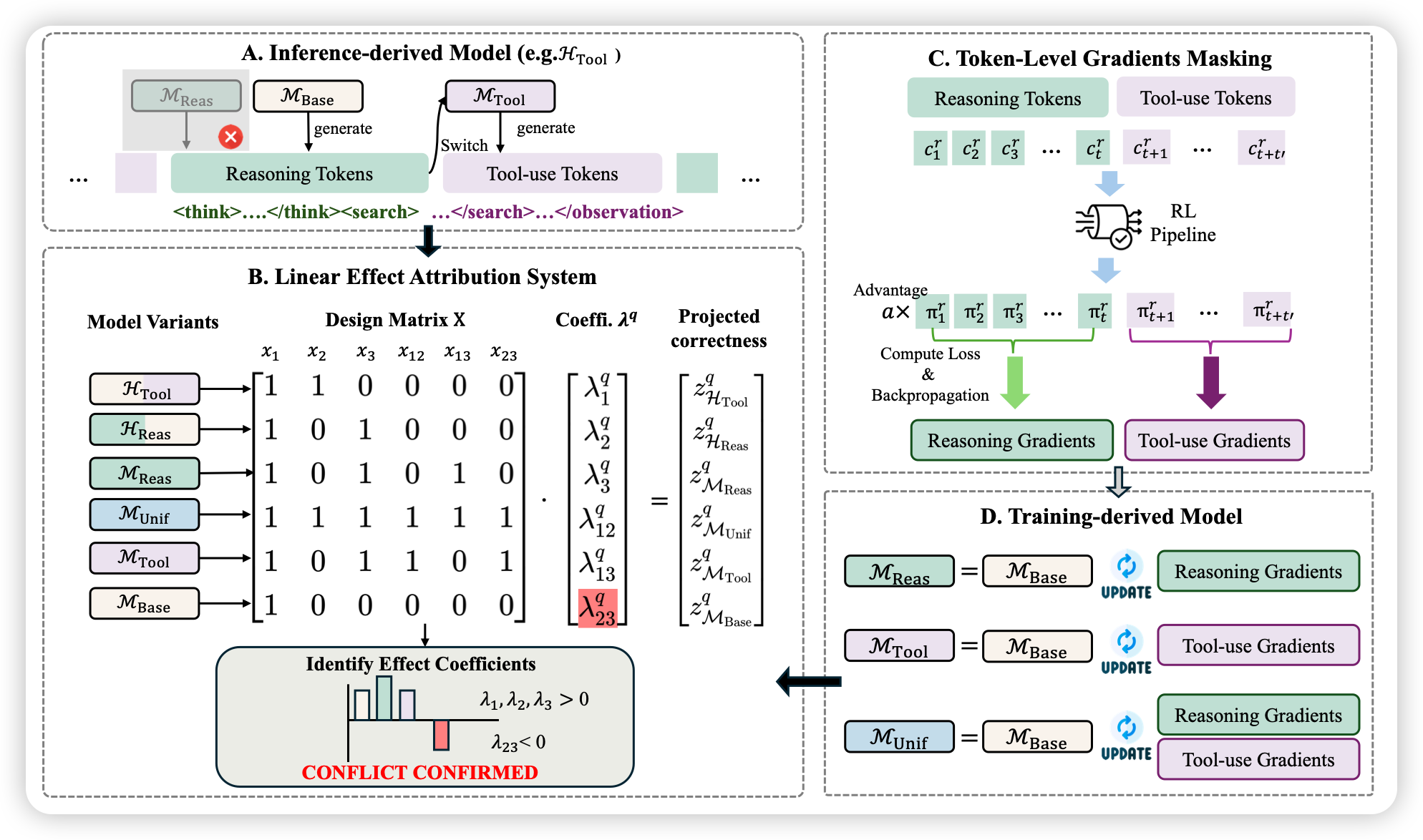
图1：LEAS框架概览。(A) 推理时混合方案；(B) 线性效应归因系统通过设计矩阵求解交互系数；© Token级梯度掩码；(D) 训练派生模型

2.2 实证发现：干扰是常态

在NQ和HotpotQA数据集上的分析显示：

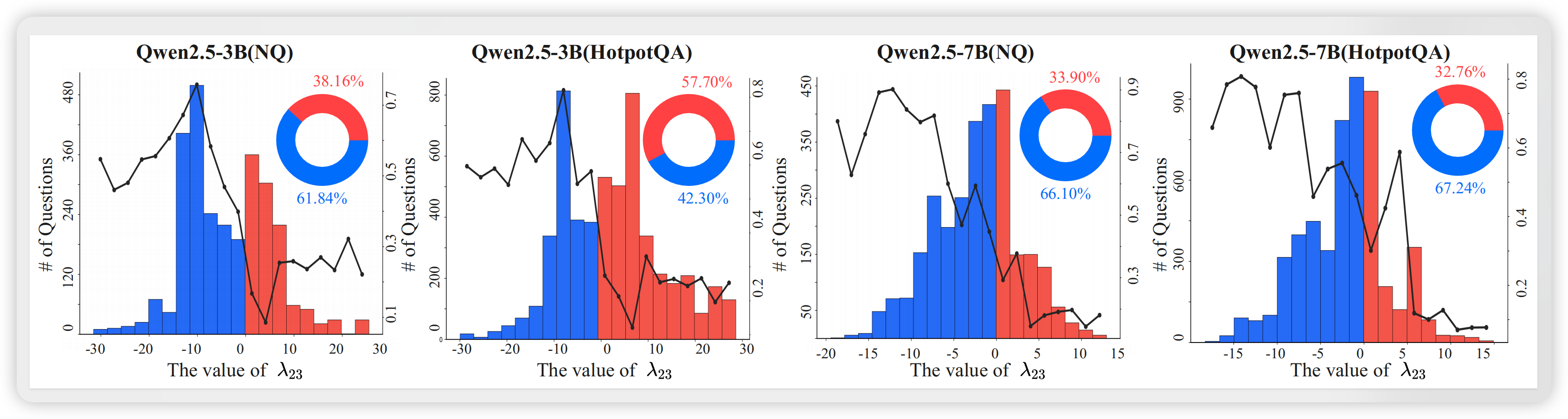
绝大多数问题的交互系数 $\lambda_{23}^q < 0$ ，表明干扰是ARL中的普遍现象
有趣的是，ARL的成功主要集中在干扰区域：需要同时使用两种能力的复杂问题，反而更容易触发参数竞争
这一现象在Qwen2.5-3B和7B模型上均得到验证，具有跨规模的稳健性

2.3 梯度冲突：干扰的根源

作者进一步分析了梯度方向的几何关系：

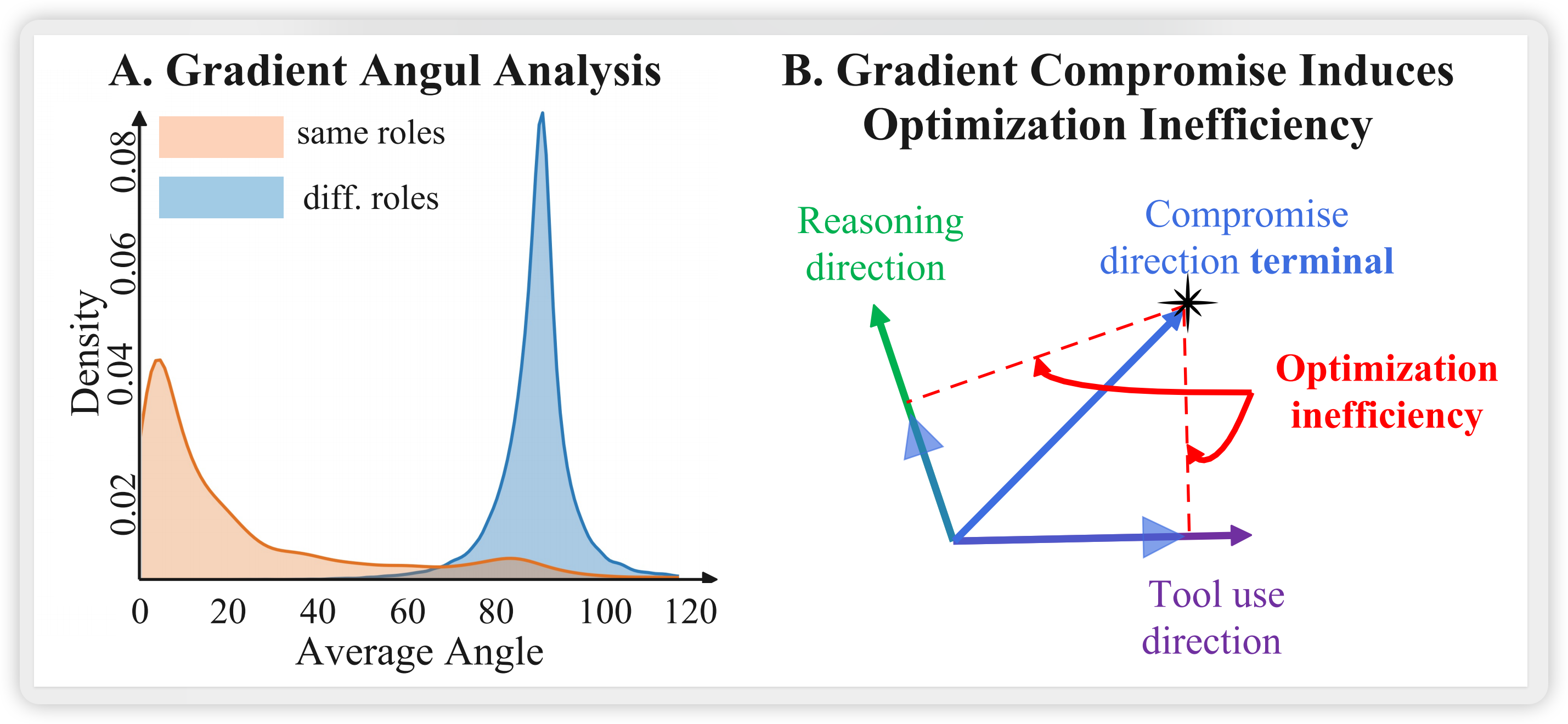
同类型梯度对齐：推理-推理、工具-工具梯度之间的夹角较小（分布集中在0度附近）
跨类型梯度正交：推理-工具梯度之间的夹角接近90度，呈正交分布

这一现象的物理含义是：两种能力在参数空间中追求截然不同的优化方向。当强制在共享参数上联合优化时，梯度更新被迫"折中"，导致双方都无法达到各自的最优解。

2.4 DART：解耦的行动-推理微调

基于上述分析，作者提出了Disentangled Action-Reasoning Tuning（DART），核心思想是在训练时显式隔离两种能力的梯度更新。

架构设计：

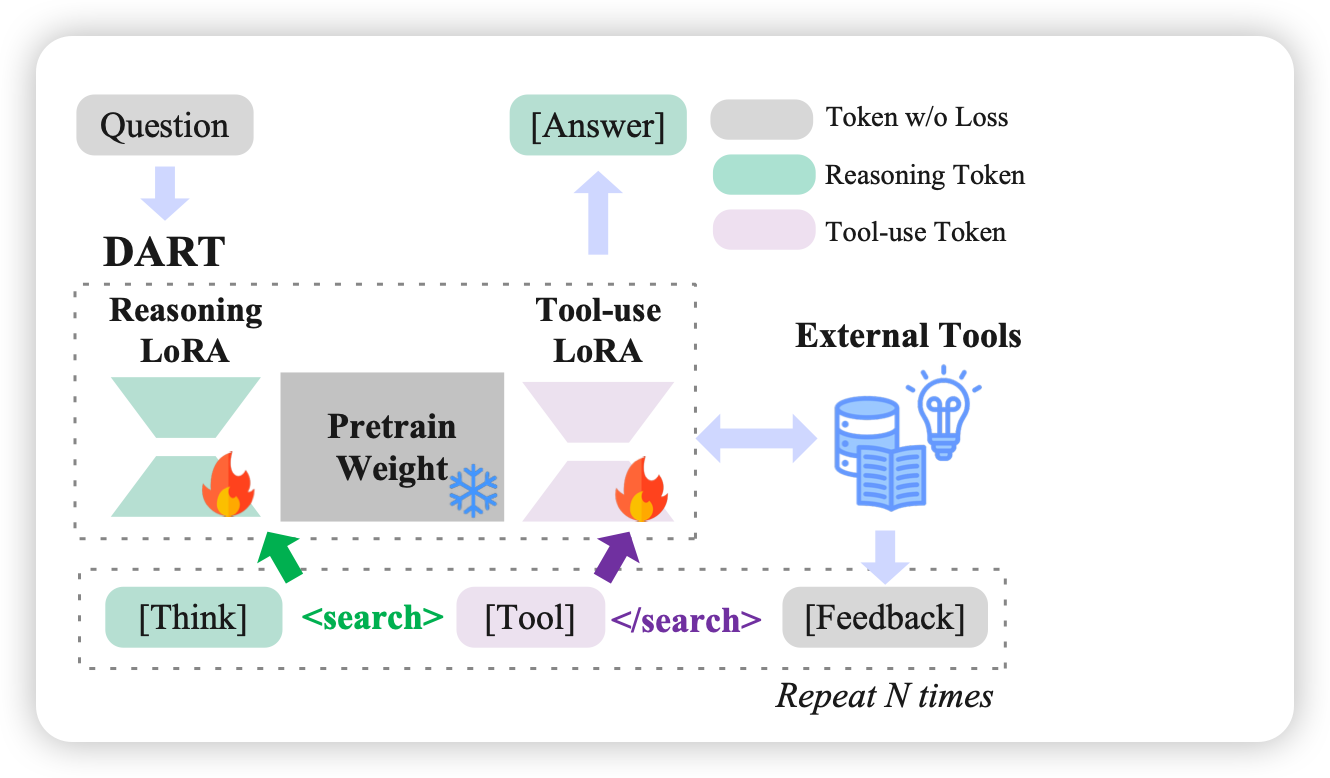
图2：DART架构示意图。冻结的backbone配备两个独立的LoRA适配器，token级路由器将梯度导向独立的参数子空间

冻结预训练backbone $W$ ，阻止梯度在共享参数上混合
引入两个独立的LoRA适配器：
- $\theta^r = \{B_r, A_r\}$ ：专用于推理token
- $\theta^a = \{B_a, A_a\}$ ：专用于工具使用token
Token级路由：根据特殊标记（如<search>触发工具LoRA）决定每个token使用的适配器

前向传播公式：

$\mathbf{h}'_t = W \mathbf{h}_t + B_{u_t} A_{u_t} \mathbf{h}_t$

其中 $u_t \in \{r, a\}$ 由路由器 $\ell(t)$ 根据token角色决定。

关键差异：

方法	参数更新方式	干扰程度
标准ARL	共享参数，联合更新	高（梯度冲突）
单LoRA	共享低秩子空间	高（子空间重叠）
DART	独立LoRA，token级隔离	零（ $x_{23}=0$ ）
2-Agent	独立模型	零（但开销翻倍）

3. 验证与实验分析 (Evidence & Analysis)

3.1 主实验结果

作者在7个工具增强QA基准上评估DART，涵盖：

General QA：NQ、TriviaQA、PopQA（单步事实检索）
Multi-Hop QA：HotpotQA、2WikiMultiHopQA、Musique、Bamboogle（多步推理）

Qwen2.5-3B-Instruct结果（EM分数）：

方法	NQ	TriviaQA	PopQA	HotpotQA	2Wiki	Musique	Bamboogle	平均
Search-R1-GRPO	0.397	0.565	0.391	0.331	0.310	0.124	0.232	0.336
DART	0.451	0.602	0.476	0.392	0.376	0.143	0.352	0.399

关键发现：

DART在3B-Instruct上平均提升 6.3% EM分数
Multi-Hop QA提升更显著（从0.249到0.316，相对提升27%），验证了复杂任务对能力解耦的更强需求
在3B-Base上提升更为显著（平均从0.303到0.405，相对提升34%）

3.2 机制分析

固定检索下的推理能力：

作者设计了一个控制实验：强制DART和Search-R1使用相同的检索结果生成答案。结果显示：

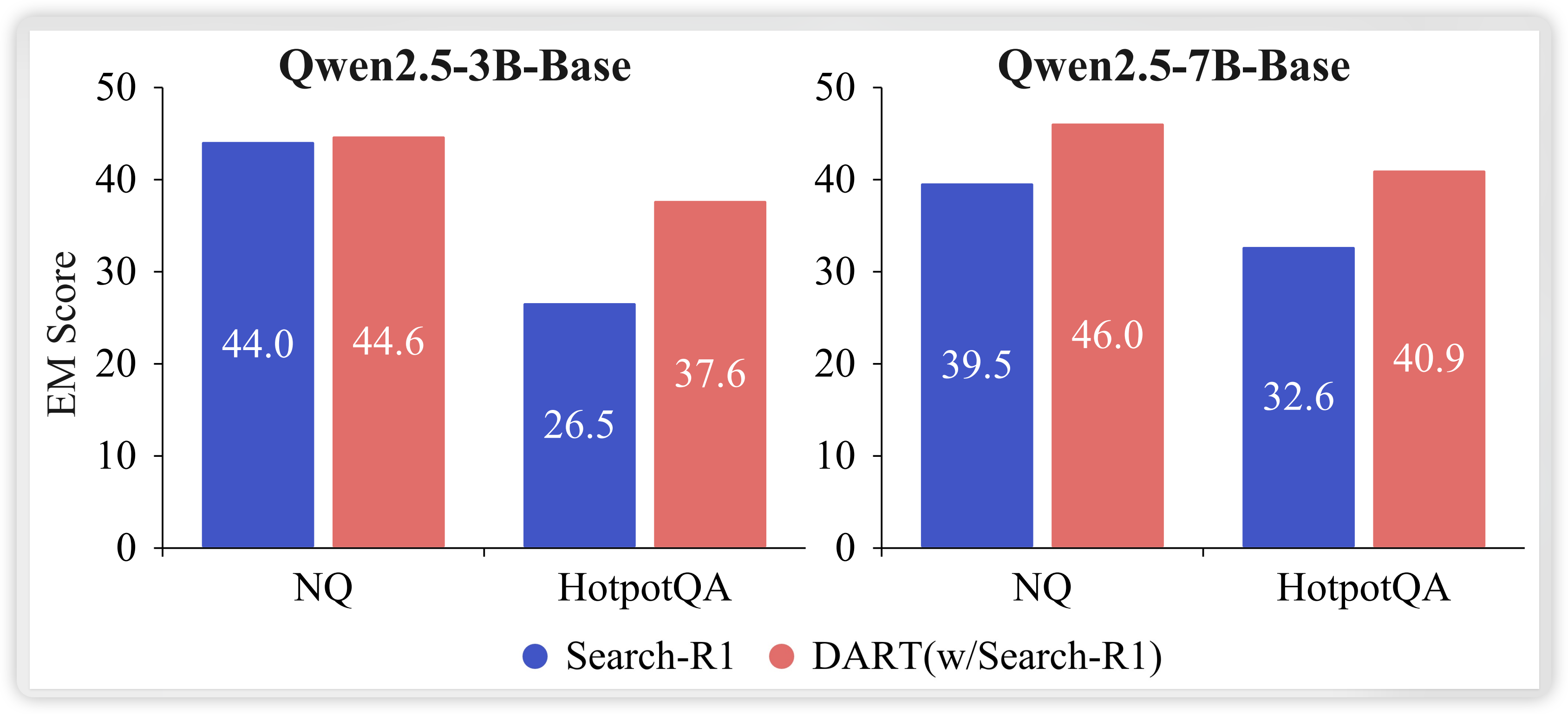
DART在固定检索上下文下的EM仍显著高于Search-R1
这表明联合训练确实损害了推理能力的学习，而DART通过训练时隔离保持了更强的推理能力

DART vs. 混合推理方案：

对比DART与LEAS中的混合推理方案（ $\mathcal{H}_{\text{Reas}}$ 、 $\mathcal{H}_{\text{Tool}}$ ）：

方法	NQ (3B)	HotpotQA (3B)	NQ (7B)	HotpotQA (7B)
$\mathcal{H}_{\text{Reas}}$	0.435	0.324	0.438	0.327
DART $_{\text{Reas}}$	0.448	0.359	0.449	0.412
$\mathcal{H}_{\text{Tool}}$	0.248	0.212	0.305	0.255
DART $_{\text{Tool}}$	0.372	0.283	0.378	0.332

结果表明：推理时混合无法复现训练时解耦带来的性能增益。DART通过端到端的联合训练使两种能力在各自参数子空间中协同进化，这是简单的推理时组合无法实现的。

3.3 消融实验

DART vs. 2-Agent系统：

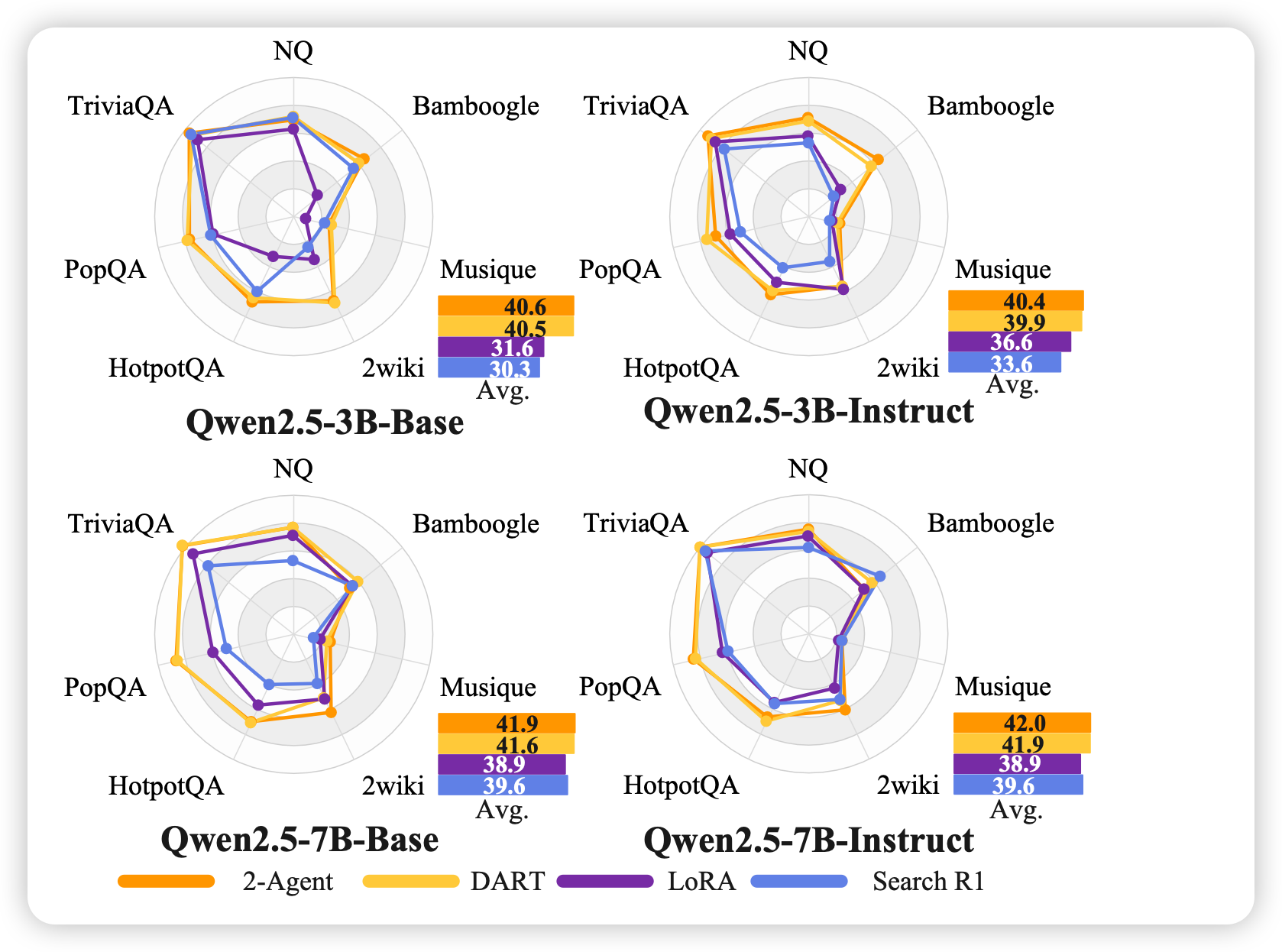
图3：DART与2-Agent系统的性能对比。DART在单模型内恢复了2-Agent系统的大部分性能优势

2-Agent系统（独立推理模型+独立工具模型）作为性能上界
单LoRA与Search-R1性能相当，证明瓶颈不在于参数容量
DART接近2-Agent性能，同时避免了多模型系统的部署开销

效率对比：

指标	2-Agent (LoRA)	DART (Multi-LoRA)
Backbone实例数	2	1
训练VRAM	$\approx 8P$	$\approx P$
上下文切换开销	高（重编码 $\mathcal{O}(L^2)$ ）	零（KV-Cache复用）

DART将训练时静态内存占用降低约 8倍，且推理时无需跨模型状态同步。

4. 局限性与落地思考 (Critical Review)

4.1 复现门槛

计算资源：实验基于8×A800 GPU集群，虽然DART降低了内存需求，但ARL训练本身仍需要较大算力
数据依赖：训练数据为NQ+HotpotQA的合并集合，对于其他领域任务需要重新收集轨迹数据
超参数敏感：LoRA学习率需要放大10倍，这一"Magic Number"来自经验性指导

4.2 潜在短板

路由规则依赖：DART依赖显式的token级路由规则（如<search>标记），对于边界模糊的能力类型（如推理中嵌套工具决策）可能需要更细粒度的设计
未探索的多能力扩展：本文仅考虑两种能力（推理+工具），对于更复杂的多工具或多能力场景，LoRA的组合方式尚不明确
缺乏理论保证：虽然实验验证了梯度隔离的有效性，但未提供收敛性或最优性的理论分析

4.3 工程落地启示

生产部署优势：DART的单模型设计大幅简化了服务架构，避免了多Agent系统的编排复杂性和状态同步开销
KV-Cache复用：在工具调用频繁的多轮交互场景中，DART的推理延迟优势将更加明显
模块化扩展：LoRA适配器的即插即用特性使得能力模块的独立迭代成为可能，支持A/B测试和灰度发布

5. 总结与启示 (The Verdict)

对研发的启示

重新审视联合训练假设：本文揭示了一个重要的设计原则——并非所有能力都适合在共享参数空间中联合优化。在Agent系统设计中，应当优先分析不同能力之间的梯度兼容性。
梯度隔离作为一种通用模式：DART的核心思想（token级梯度隔离）可以推广到更广泛的多任务学习场景。当检测到任务间存在梯度冲突时，参数空间解耦往往比复杂的损失加权或梯度修正更有效。
LoRA的潜力被低估：传统上LoRA被视为参数效率工具，但DART展示了其在能力解耦方面的独特价值。通过为不同能力分配独立的低秩子空间，可以在保持模型紧凑的同时实现功能模块化。