GPT,也就是 Transformer Decoder 结构做文本生成时有一个致命问题。先来看看 Encoder 推理是怎么做的,每个 timestep 都能看到所有 timestep ,推理时所有 timestep 一层层向后计算,一把过。于是内存相关开销就是 , 而计算相关开销就是 ,其中 N 为序列长度。
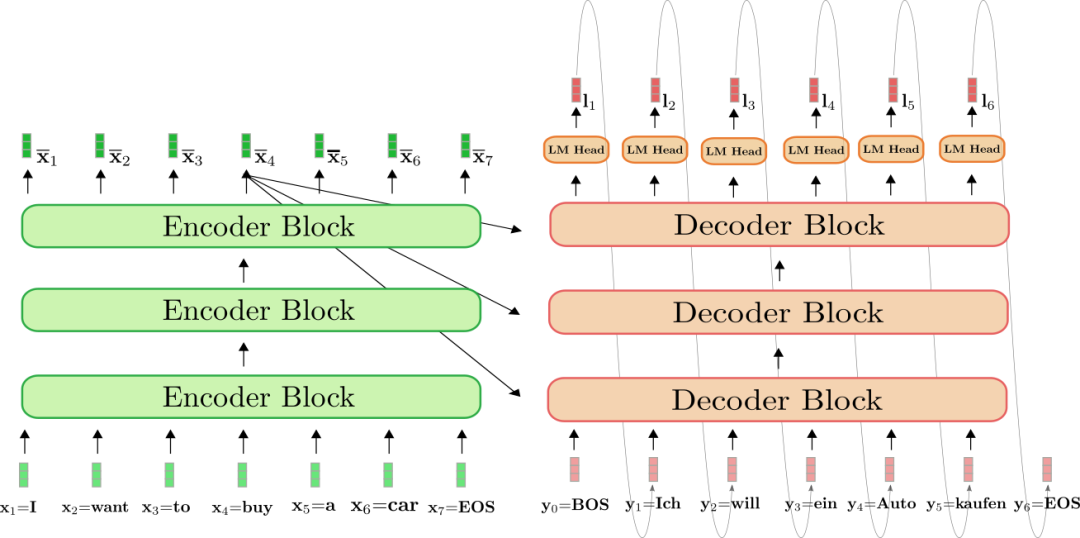
而 Decoder 推理时,最大不同在于自回归结构,可以看到图中每个 timestep 的输出都是下一 timestep 的输入,所以无法像 Encoder 一样一次过,每次都要 attend 之前的所有 timestep.
同样计算一下开销,计算开销是 也就是 ,而内存开销则是 .
大家用 ChatGPT 接口也会有类似感觉,Context 部分成本很低,也很快,因为它做的类似于 Encoder 的并行。主要成本在生成那块,速度较慢,但也已经是优化过后的了。
下面就来讲讲优化方法。
KV Cache
Decoder 每次前向,当前 timestep 计算 Attention 要用到的部分,如之前 timestep 的 KV (Key 和 Value)值都计算过的,只是之前每次前向完后给计算结果都丢掉,只保留最后输出。
于是一个很自然的想法就是 Cache。这很像斐波那契递归函数,naive 版本,也会出现不断重复计算问题,加个 cache 瞬间提速。
每次前向完,给 KV 都保留下来,用于之后计算。
代码表示如下:
1 | #q、k、v 当前 timestep 的 query,key,value |
于是 Decoder 就被优化成,计算开销变成了,存储复杂度则是 ,只给 K 和 V 不断保存在缓存中就行。问题解决了!
但残酷现实会立马跳出来给你一棒子,上面假设 K 和 V 能直接存在缓存中,模型规模小还好,一旦模型规模很大长度很长时,KV 根本就存不进缓存。
比如 Llama 7B 模型,hidden size 是 4096,那么每个 timestep 需缓存参数量为 4096232=262144,假设半精度保存就是 512KB,1024 长度那就要 512MB. 而现在英伟达最好的卡 H100 的 SRAM 缓存大概是 50MB,而 A100 则是 40MB. 而 7B 模型都这样,175B 模型就更不用说了。
那为什么我们不直接做大 SRAM 内存呢,不就直接解决问题了吗,但是这样又会产生一个新问题 SRAM 太贵了,所以这条路现在是不太行的。
于是退一步,放不进缓存可以放 DRAM 上去,而 DRAM 内存也就是我们常说的 GPU 显存。
但 DRAM 读取到计算芯片和 SRAM 到计算芯片的速度,差了一个量级的,这会让计算芯片一直在等待。
SRAM是静态随机存储器,速度非常快,但成本较高。DRAM是动态随机存储器,成本较低,但速度比SRAM慢
现在我们遇到了当今芯片领域,冯诺依曼架构下最大的一个问题,也就是:Memory Wall(内存墙)。
冯诺依曼架构和 Memory Wall
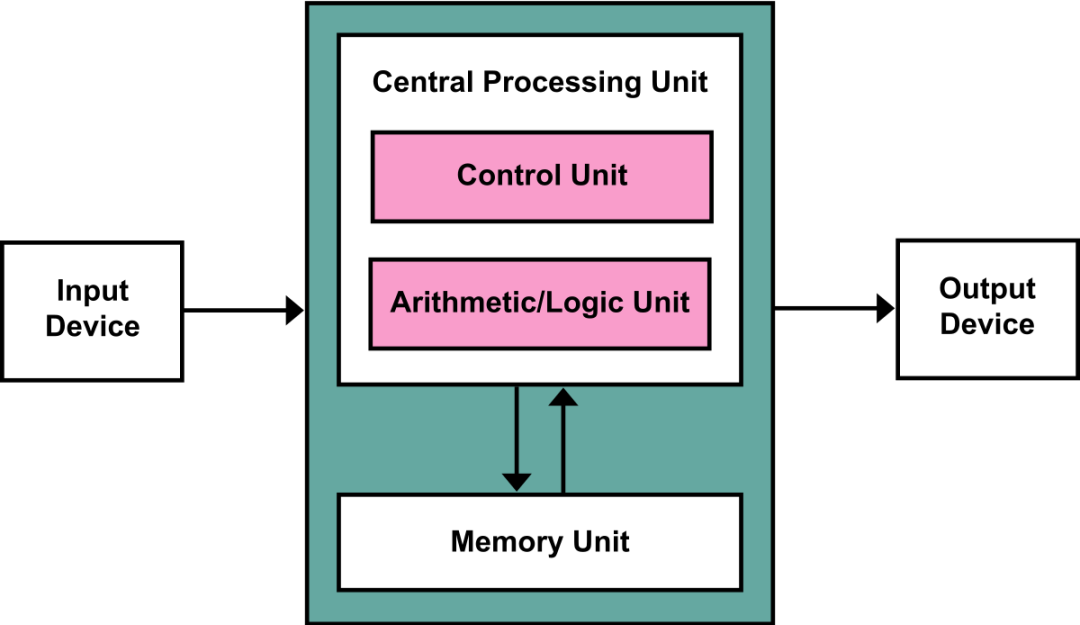
冯诺依曼架构熟悉有计算机相关基础的,应该都稔熟于胸。输入,输出,计算单元,加上存储单元。
现在随着摩尔定律的见顶,虽然计算和内存的发展速度在变缓,但这并不是最大的问题,最大的问题是存储单元与计算单元间的交互。
冯诺依曼架构需要先从内存中调取数据,送入计算单元进行处理,但现在计算单元的速度是显著提升的,而从内存中读取数据的速度却没跟上,所以计算和内存这里就形成了一个瓶颈。因为短板效应,内存读取速度限制了整体速度。计算单元能很快将数据处理完,但新数据却还没到,于是就只能等待,造成利用率不高。这就是内存墙。
因为内存墙问题,现在 GPU,一张 A100 卡计算单元的利用率到四五十就不错了,用上各种技巧优化到 60% 已经很高了。而对于 H100 卡问题会更严重,因为它的计算速度相对 A100 提高了 6 倍,而内存读取带宽只增加了 1.6 倍,所以也要大量优化来提高利用率。
内存墙怎么越过呢?
硬件层面上,比如现在已在使用的 HBM(高速带宽内存)提高读取速度,或者更彻底些,抛弃冯诺依曼架构,改变计算单元从内存读数据的方式,不再以计算单元为中心,而以存储为中心,做成计算和存储一体的“存内计算”。
软件层面上的话,最近的很多优化,比如 Flash Attention,Paged Attention 都可以算。Flash Attention 就是减少了计算 Softmax 时从 DRAM 内存读取数据次数,从而提高了效率。
Flash Attention算法背后的主要思想是分割输入,将它们从慢速HBM加载到快速SRAM,然后计算这些块的 attention 输出。在将每个块的输出相加之前,将其按正确的归一化因子进行缩放,从而得到正确的结果。
vLLM 主要用于快速 LLM 推理和服务,其核心是
Paged Attention同样,MQA 也是一个软件层面上翻墙的一个方法。这是一种受操作系统中虚拟内存和分页经典思想启发的注意力算法。与传统的注意力算法不同,Paged Attention允许在非连续的内存空间中存储连续的 key 和 value 。具体来说,Paged Attention将每个序列的 KV cache 划分为块,每个块包含固定数量 token 的键和值。在注意力计算期间,Paged Attention内核可以有效地识别和获取这些块。
MHA 到 MQA 到 GQA
MQA 的方法很简单,难的是看到这样的方法后,能立刻想到它为什么好。
一起看看 MQA 和 GQA 是怎么来的。
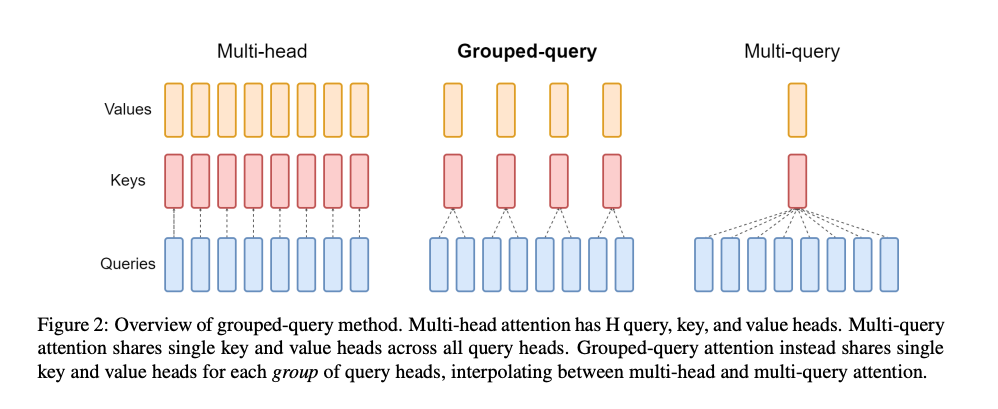
首先是原始的 MHA(Multi-Head Attention),QKV 三部分有相同数量的头,且一一对应。每次做 Attention,head1 的 QKV 就做好自己运算就可以,输出时各个头加起来就行。
1 | # 为了方便阅读,我们只保留了 llm-foundry 中关键部分的代码,完整代码请参照源码。 |
而 MQA(Multi-Query Attention) 则是,让 Q 仍然保持原来的头数,但 K 和 V 只有一个头,相当于所有的 Q 头共享一组 K 和 V 头,所以叫做 Multi-Query 了。实现改变了会不会影响效果呢?确实会影响但相对它能带来的收益,性能的些微降低是可以接受的。
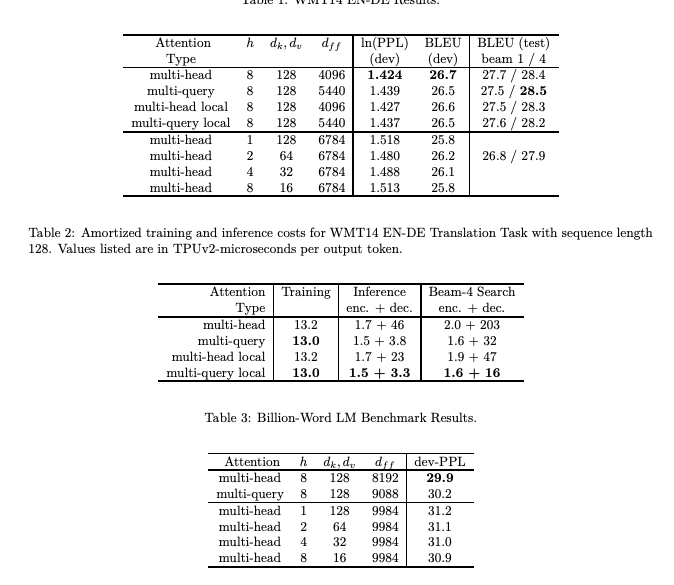
从上图表中可以看到,MQA 在 encoder 上的提速没有非常明显,但在 decoder 上的提速是很显著的,能带来多大的收益呢,实验发现一般能提高 30%-40% 的吞吐。
收益主要就是由降低了 KV cache 带来的。实际上 MQA 运算量和 MHA 是差不多的,可理解为读取一组 KV 头之后,给所有 Q 头用,但因为之前提到的内存和计算的不对称,所以是有利的。
1 | class MultiQueryAttention(nn.Module): |
从上面的代码中可以看到,MHA 和 MQA 之间的区别只在于建立 Wqkv Layer 上:
1 | # Multi Head Attention |
而 GQA(Grouped-Query Attention) 呢,是 MHA 和 MQA 的折衷方案,既不想损失性能太多,又想获得 MQA 带来的推理加速好处。具体思想是,不是所有 Q 头共享一组 KV,而是分组一定头数 Q 共享一组 KV,比如上面图片就是两组 Q 共享一组 KV。
LLAMA2 中给出了效果对比,可以看到相比起 MQA,GQA的指标看起来还是要好些的。
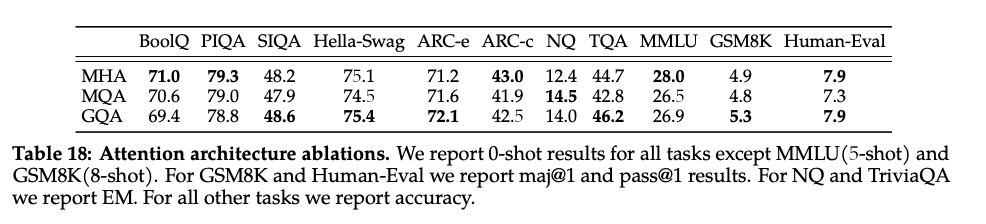
同时在推理上的加速还和 MQA 类似:
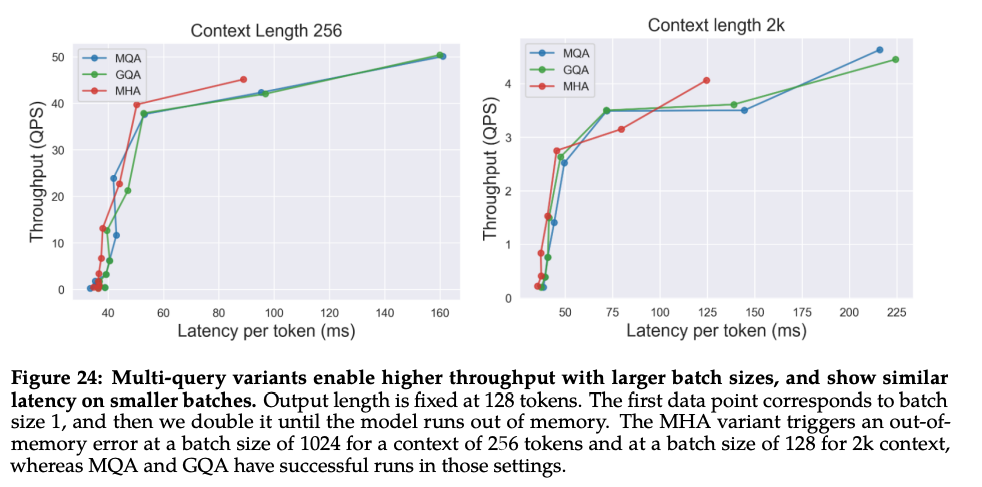
MQA 和 GQA 形式在推理加速方面,主要是通过两方面来完成:
- 降低了从内存中读取的数据量,所以也就减少了计算单元等待时间,提高了计算利用率;
- KV cache 变小了 head_num 倍,也就是显存中需要保存的 tensor 变小了,空出来空间就可以加大 batch size,从而又能提高利用率。
如果要用 MQA 和 GQA,可以是从头训练的时候就加上,也可以像 GQA 论文里面一样,用已有的开源模型,挑一些头取个 mean 用来初始化 MQA 或 GQA 继续训练一段时间。
下面是 MQA 推导过程,不感兴趣同学可跳过,感兴趣同学可推一下,理解更透彻。
MQA 的推导
正如在 memory wall 中提到的,现在内存读取相对计算速度太慢导致拖后腿。
那么定义一个变量,, M 是 Memory 表示内存开销,而 A 是 Arithmetic 表示计算开销。如果这个值大于1的话,就会出现很明显的 Memory Wall,而当这个值小于1很多时,表示拿到数据后马上能开动马力计算,内存墙问题就不存在了。因为估算还有各种没考虑因素问题,所以即使等于 1 也不代表就能打满计算单元。
那么先来看看 MHA 下推理时每一个 timestep 这个值的大小,主要参考 MQA 原论文的简化:
1 | #三个投影矩阵分别为 P_q, P_k, P_v; 维度为 h(头数), a(隐层大小,等于hd), d(每个头大小) |
所以对于 M 来说是
对于 A 来说
假设隐层大小和 timestep 数接近,, 那么 A 就是 , 因此
可以看到要想让这个比例小,可以增大b,也就是增大 batch size,现在推理优化就会将用户的请求收集成 batch 推理,提高利用率。同时前面提到,MQA 可以降低显存使用扩大 batch size,所以能提高一定利用率。
根据假设 ,这个比例会接近 1,会导致一定 Memory Wall,如果 n 很长的话问题就更明显。
而 MQA 的情况下
1 | #投影矩阵 P_k, P_v 维度变为 a(隐层大小,等于hd), d(每个头大小) |
会发现 A 整体来说没有变,如之前说的只是共享了 KV, 计算量还是一样的 ,M 变化比较大
于是系数为
其中后面两项,d 一般比 h 要大,所以可以主要考虑 项。可看到之前占大头的 在分母加了个系数 h,这样就能降低 从而提高效率。
感兴趣的话,可自己推导一下 GQA 的情况,其中 的分母中会加入一个数 , 其中 g 为 group 数,如果 g 为 1 的情况那就和 MQA 一样了,这块开销主要就有 g 来调整了。
再见美好旧时光
看到这,大概也能明白为什么要用 MQA 了,以及为什么 MQA 最近才突然火起来。
主要就是因为大规模 GPT 式生成模型的落地需求导致的。
而在以前根本不需要关心这些,LSTM 只用维护一个状态,不存在要保留 Cache 什么。
到了 Transformer 提出后,虽然最早 Transformer 提出时是用在 Seq2Seq 任务上,也就是 Encoder 和 Decoder 都用,但可能模型量级不大,也没有太多落地需求,所以没引起太大关注。之后火了两年的 BERT 又是 Encoder 结构,直接前向一把过。
也只有到最近 GPT 大模型得到广泛应用时,才发现推理的这个瓶颈,于是大家翻出几年前的 trick,应用起来,发现非常好用。
同样原因,GPT 推理加速这块最近引起很多关注,大家都在想各种方法来提高推理效率。Huggingface 这两天也给 text-generation-inference 库的 license 给改了,应该也是想用这个挣点钱。