Pointer Networks

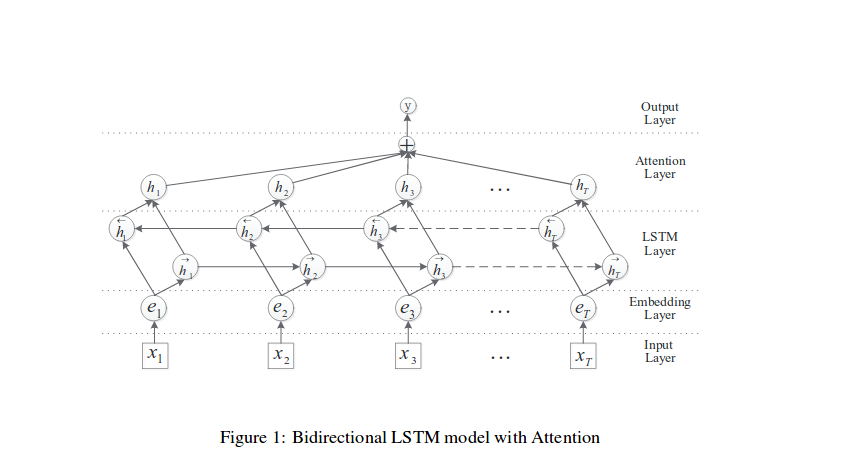
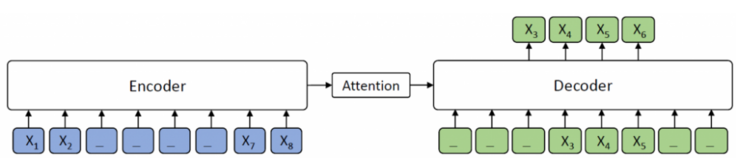
我们知道，Seq2Seq的出现很好地解开了以往的RNN模型要求输入与输出长度相等的约束，而其后的Attention机制（content-based）又很好地解决了长输入序列表示不充分的问题。尽管如此，这些模型仍旧要求输出的词汇表需要事先指定大小，因为在softmax层中，词汇表的长度会直接影响到模型的训练和运行速度。

Pointer Networks（指针网络）同样是Seq2Seq范式，它主要解决的是Seq2Seq Decoder端输出的词汇表大小不可变的问题。换句话说，传统的Seq2Seq无法解决输出序列的词汇表会随着输入序列长度的改变而改变的那些问题，某些问题的输出可能会严重依赖于输入，在本文中，作者通过计算几何学中三个经典的组合优化问题：凸包（Finding convex hulls）、三角剖分（comupting Delaunay triangulations）、TSP（Travelling Salesman Problem），来演示了作者提出的PtrNets模型。

论文地址: https://arxiv.org/pdf/1506.03134.pdf

上图，我们求解凸包问题，模型输入是所有点的坐标，输出是构成凸包的点的合集。无法使用传统的seq2seq模型进行建模，因为，我们并不知道输出的数据的多少。更具体地说，就是在 encoder 阶段，我们只知道这个凸包问题的输入，但是在 decoder 阶段，我们不知道我们一共可以输出多少个值。举例来说就是，第一次我们的输入是 50 个点，我们的输出可以是 0-50 (0 表示 END)；第二次我们的输入是 100 个点，我们的输出依然是 0-50, 这样的话，我们就没办法输出 51-100 的点了。

方法

seq2seq模型

给定训练数据集对$(P, C^P)$, $P={P_1,P_2,.....,P_N}$为n个向量序列，$C^P={C_1,C_2,....,C_{m(P)}}$为$m(P)$个下标的序列，每一个在1到n之间，seq2seq模型计算条件概率$p(C^P | P, \theta)$，根据概率链式法则有：

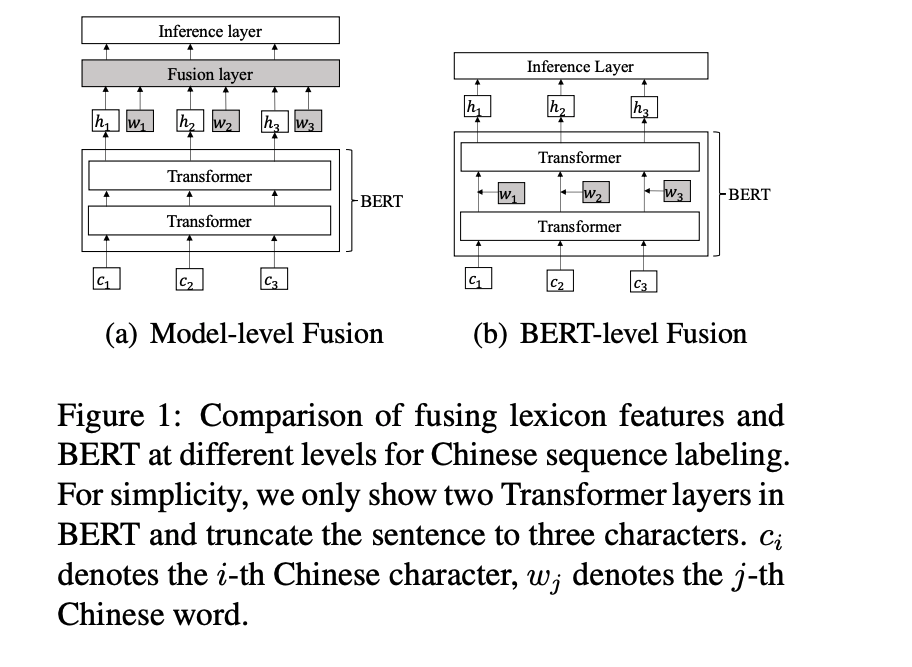
然后通过最大训练集的条件概率来学习模型的参数：

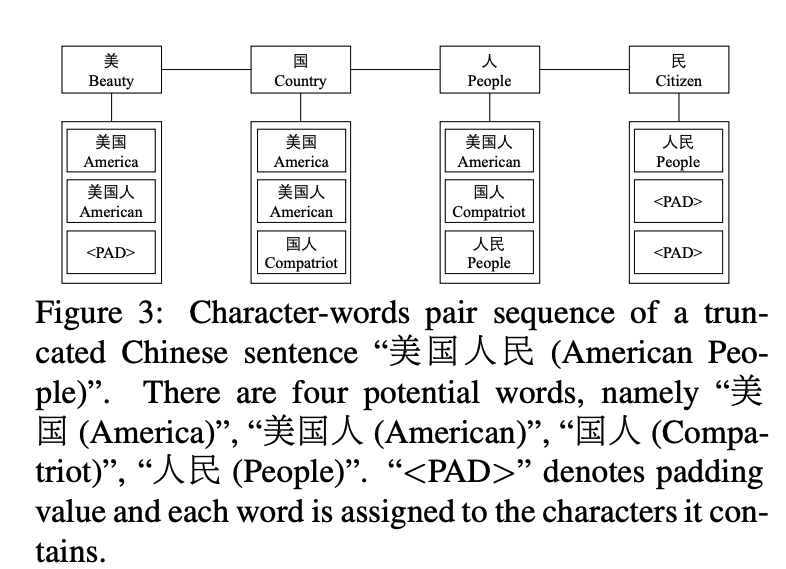
在预测阶段，对于给定序列P，利用学习到的参数$\theta$来选择概率最大的序列:

seq2seq模型分成Encoder和Decoder两个部分。定义Encoder和Decoder的隐藏状态为 $(e_1,.....,e_n)$和 $(d_1,.....,d_{m(P)})$。在Encoder部分，每个时间步 $i$ ，利用输入的序列元素 $P_i$ 以及上一个时间步的隐藏状态 $e_{i-1}$ 生成当前时间步的隐藏状态 $e_i$ 。直到输入START，表示输入序列结束。此时的隐藏状态 $e_n$ 是context vector，包含整个输入序列的信息。接着就是Decoder部分，它将Encoder部分得到的context vector作为输入，每一步根据上一步的预测结果进行预测，直到输出END表示输出序列结束。

Seq2Seq+Attention模型

在Seq2Seq模型中，Decoder部分的预测是根据包含整个输入序列信息的context vector进行预测的，注意力机制就是让Decoder在每一步预测输出单词时，重点关注输入序列中对该步预测影响力大的那些单词。

计算每个输出时间步 $i$ 的注意力向量：

其中向量 $v$和矩阵 $W_1$ 、 $W_2$ 是可学习参数。最后将 d_i^' 和 $d_i$ 拼接在一起作为Decoder第 $i$ 个时间步的隐藏状态，并进行预测。

Pointer Networks

无论是原始的Seq2Seq模型还是Seq2Seq+Attention模型，对于组合优化问题输出序列字典长度取决于输入序列长度的问题，都需要针对不同的输入序列长度重新训练模型。由于注意力机制能够得到对于当前预测时间步权重最大(影响力最大)的输入序列元素，所以Pointer Networks直接将权重最大的这个输入序列元素预测为输出。公式就对应修改为：

可以看到公式类似seq2seq+Attention模型中的attention，不一样的是这里的attention 是根据输入的点去算一个分布，然后将 arg max 的点作为输出，也就是当前这个凸包问题的解的点，一直 train 下去，直到输出的点是 END。为了避免理解上出现偏差，这里再用一个例子解释一遍。
模型一共是 encoder 和 decoder 两个部分。 刚开始 encoder 将所有输入训练完毕， 在 decoder 部分，刚开始输入一个 $z_0$ 作为初始变量，然后 $z_0$ 会去跟 encoder 中所有的点做一个 attention operation, 得到的结果是一个分布，正常情况下我们会对这个分布做 weigted sum，但是在这里，我们对这个分布做一个 arg max 取出概率最大的点(假设这个点是 1)。然后这个点$(x_1,y_1)$ 和 $z_0$ 又会作为新一轮输入，扔进 decoder 里面得到 $z_1$，然后 $z_1$ 又会跟 encoder 中所有的点做一个 attention operation 得到另一个新的分布，同样再取出概率最大的点，如此反复，直到取到的点是 0 (0 表示 END)

实验结果

见原论文