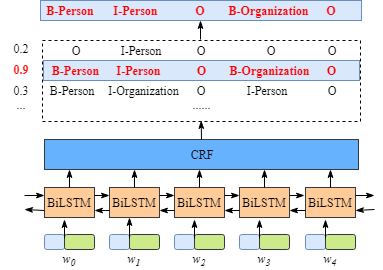
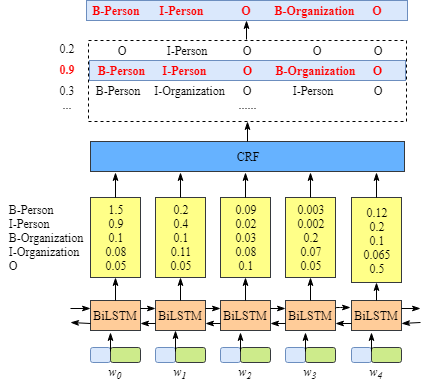
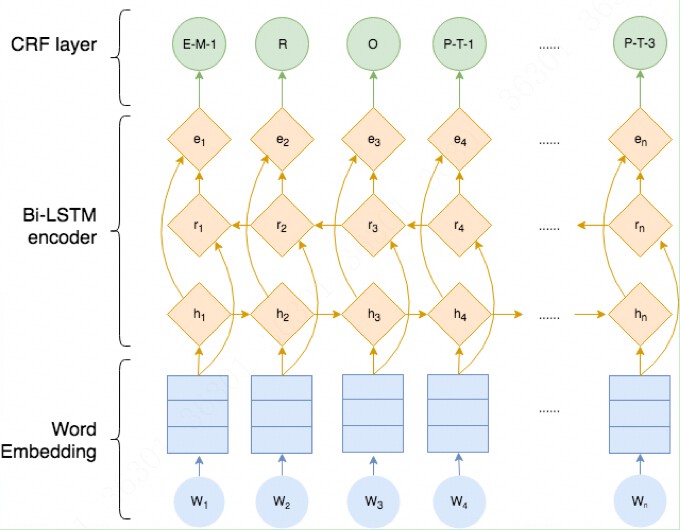
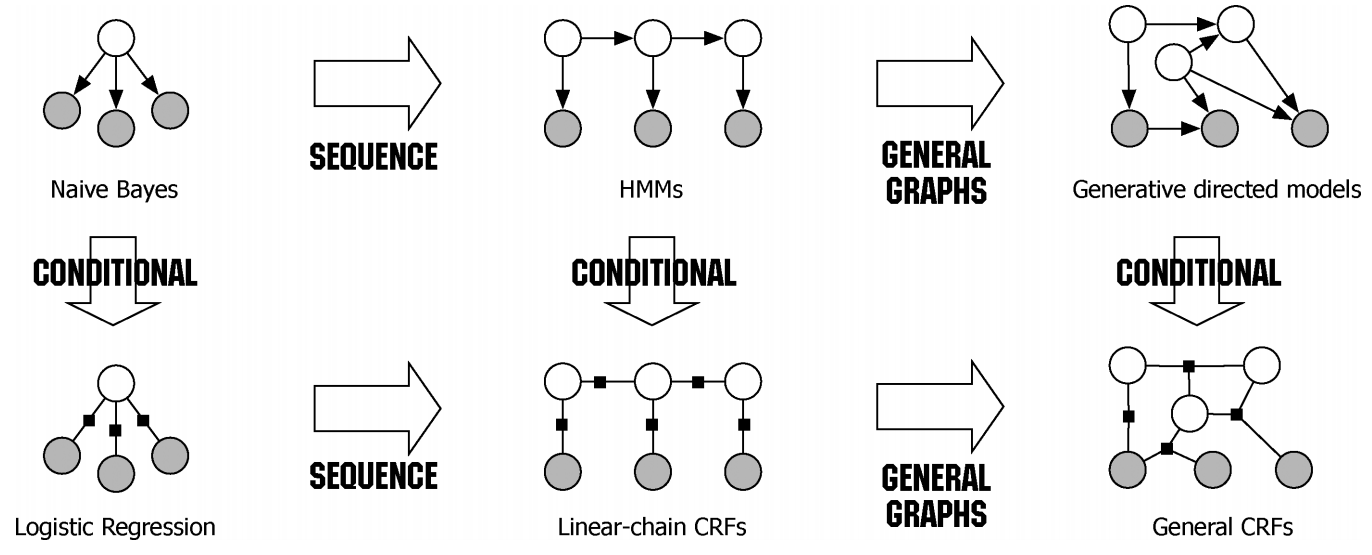
在前面的部分中,我们学习了BiLSTM-CRF模型的结构和CRF损失函数的细节。您可以通过各种开源框架(Keras,Chainer,TensorFlow等)实现您自己的BiLSTM-CRF模型。最重要的事情之一是在这些框架上自动计算模型的反向传播,因此您不需要自己实现反向传播来训练模型(即计算梯度和更新参数)。此外,一些框架已经实现了CRF层,因此只需添加一行代码就可以非常轻松地将CRF层与您自己的模型相结合。
在本节中,我们将探讨如何预测句子的标签序列。
1. 预测句子的标签序列
第1步:BiLSTM-CRF模型的emission score和transition score
假设句子x包含3个字符:x=[w0,w1,w2]。此外,假设我们已经获得了BiLSTM模型的emission score和CRF层的transition score:
|
l1 |
l2 |
| w0 |
w01 |
w02 |
| w1 |
w11 |
w12 |
| w2 |
w21 |
w22 |
xij表示wi被标记为lj的得分。
|
l1 |
l2 |
| l1 |
t11 |
t12 |
| l2 |
t21 |
t22 |
tij表示标签i转移到标签j的分数
第2步:预测
如果您熟悉Viterbi算法,这部分对您来说很容易。如果你不太了解的话,请不要担心,我将逐步解释算法。对于一个句子,我们将按从左到右的方式进行预测,即:
w0
w0–>w1
w0–>w1–>w2
你将看到两个变量:obs和previous。previous存储前面步骤的最终结果。obs表示来自当前单元的信息。
首先,我们来看看w0,即:
obs=[x01,x02]
previous=None
对于第一个字符w0。w0的最优标签很简单。例如,如果obs=[x01=0.2,x02=0.8],显然,w0的最优标签是l2,由于只有一个字符从而无标签到标签之间的transition,因此不用计算transition scores。
接着,对于w0 --> w1:
obs=[x11,x12]
previous=[x01,x02]
1).扩展previous为:
previous=(previous[1]previous[1]previous[0]previous[0])=(x02x02x01x01)
2).扩展obs为:
obs=(obs[0]obs[1]obs[0]obs[1])=(x11x12x11x12)
3).将previous,obs和transition score进行求和:
scores=(x02x02x01x01)+(x11x12x11x12)+(t21t22t11t12)
即:
scores=(x02+x11+t21x02+x12+t22x01+x11+t11x01+x12+t12)
当我们计算所有可能标签序列组合的总得分时,您可能想知道与前一部分没有有区别。接下来我们将看到其中的差异性。
更新previous值:
previous=[max(scores[00],scores[10]),max(scores[01],scores[11])]
假设,我们得到的score为:
scores=(x02+x11+t21x02+x12+t22x01+x11+t11x01+x12+t12)=(0.50.40.20.3)
则previous将更新为:
previous=[max(scores[00],scores[10]),max(scores[01],scores[11])]=[0.5,0.4]
previous是什么意思?previous列表存储当前字符对每个标签的最大得分。
1.1 案例
假设,在语料库中,我们总共有2个标签,label1(l1)和label2(l2),这两个标签的索引分别为0和1。
previous[0]是以第0个标签l1结束的序列的最大得分,类似的previous[1]是以l2结束的序列的最大得分。在每次迭代过程中,我们仅仅保留每个标签对应的最优序列的信息(previous=[max(scores[00],scores[10]),max(scores[01],scores[11])])。分数较少的序列信息将被丢弃。
回到我们的主要任务:
同时,我们还有两个变量来存储历史信息(分数和索引),即alpha0和alpha1。
每次迭代,我们都将最好的得分追加到alpha0。为方便起见,每个标签的最高分都有下划线。
scores=(x02+x11+t21x02+x12+t22x01+x11+t11x01+x12+t12)=(0.50.40.20.3)
alpha0=[(scores[10],scores[11])]=[(0.5,0.4)]
另外,相应的列的索引被保存在alpha1:
alpha1=[(ColumnIndex(scores[10]),ColumnIndex(scores[11]))]=[(1,1)]
其中,l1的索引是0,l2的索引是1,所以(1,1)=(l2,l2),这意味着对于当前的单元wi和标签l(i):
(1,1)=(l2,l2)=(当序列是l(i−1)=l2−>l(i)=l1时我们可以得到最大得分为0.5, 当序列是l(i−1)=l2−>l(i)=l2时我们可以得到最大得分为0.4)
l(i−1)是前一个字符wi−1对应的标签
最后,我们计算w0 --> w1 --> w2:
obs=[x21,x22]
previous=[0.5,0.4]
1).扩展previous为:
previous=(previous[1]previous[1]previous[0]previous[0])=(0.40.40.50.5)
2).扩展obs为:
obs=(obs[0]obs[1]obs[0]obs[1])=(x21x22x21x22)
3).对previous,obs和transition score进行求和:
scores=(0.40.40.50.5)+(x21x22x21x22)+(t21t22t11t12)
即:
scores=(0.4+x21+t210.4+x22+t220.5+x21+t110.5+x22+t12)
更新previous为:
previous=[max(scores[00],scores[10]),max(scores[01],scores[11])]
比如,我们得到的scores为:
scores=(0.80.70.60.9)
因此,previous将更新为:
previous=[0.8,0.9]
实际上,previousp[0]和previous[1]之间的较大的一个是最好的预测结果的得分。与此同时,每个标签的最大得分和索引将被添加到alpha0和alpha1中:
alpha0=[(0.5,0.4),(scores[10],scores[01])]
=[(0.5,0.4),(0.8,0.9)]
alpha1=[(1,1),(1,0)]
第3步:找出得分最高的最佳序列
在该步骤中,我们将根据previousp[0]和previous[1]找到最高的得分。我们将从右到左的方式反推最优序列,即最后一个单元反推到第一个单元。
w1 --> w2:
首先,检查alpha0和alpha1最后一个元素:(0.8, 0.9)和(1, 0)。0.9是最高分数,其对应的位置是1,因此对应的标签是l2。继续从alpha1中对应位置获得w1对应的标签索引, 即(1, 0)[1]=0。索引0表示w1对应的标签是l1。因此我们可以得到w1−>w2的最佳序列是l1−>l2。
w0 --> w1:
接着,我们继续向前移动并获得alpha1的上一个元素:(1, 1)。从上面可知w1的标签是l1(标签对应的索引为0),因此我们可以得到w0对应的标签索引为(1,1)[0]=1。所以我们可以得到w0−>w1的最佳序列是l2−>l1。
最终可以得到w0−>w1−>w2的最佳标签序列是l2−>l1−>l2
参考
[1] Lample, G., Ballesteros, M., Subramanian, S., Kawakami, K. and Dyer, C., 2016. Neural architectures for named entity recognition. arXiv preprint arXiv:1603.01360.
https://arxiv.org/abs/1603.01360